FVA-Workbench KnowledgeBase

Mit der Bezeichnung Lagerhauptgeometrie sind geometrische Daten gemeint die in den Katalogen der Lagerhersteller verfügbar sind. Im Wesentlichen beschränkt sich dies auf folgende (für die Berechnung relevanten) Parameter:

Für die Berechnung der Wälzlagersteifigkeit und -lebensdauer ist die Kenntnis der Innengeometrie des Lagers (Anzahl Wälzkörper, Wälzkörperdurchmesser, ...) eine notwendige Voraussetzung. In den Katalogen der Wälzlagerhersteller fehlen jedoch die Angaben zur Innengeometrie, so dass die Innengeometrie des Lagers geschätzt werden muss. Wenn der Benutzer die Innengeometrie des Wälzlagers nicht explizit definiert, wird die Innengeometrie von der FVA-Workbench auf der Grundlage der verfügbaren Lagerkatalogdaten geschätzt.

Algorithmus zur Schätzung der Lagerinnengeometrie: Die Normen ISO 281 2007 und ISO 76 2006 legen Formeln zur Bestimmung der dynamischen und statischen Tragzahlen von Wälzlagern auf Basis von Innengeometriegrößen fest. Der Algorithmus zur Schätzung der Lagerinnengeometrie berechnet in einem iterativen Verfahren auf Basis geschätzter Geometriegrößen die zugehörigen Tragzahlen und vergleicht diese mit den Tragzahlen aus dem Katalog. Falls die Differenz zwischen berechneter und gegebenen Tragzahlen nicht kleiner als die Abbruchtoleranz ist wird die Geometrieschätzung geeignet angepasst und eine neue Iteration gestartet. Wesentliche Variablen der Iteration sind Anzahl und Durchmesser der Wälzkörper sowie die effektive Rollenlänge bei Rollenlagern. Die Idee des Algorithmus basiert auf dem Ansatz aus FVA 364. Dieser wurde allerdings durch zusätzliche Konsistenzprüfungen (Keine Überlappung der Wälzkörper, etc.) verbessert. Wie im Abschlussbericht von FVA 364 II Seite 20 beschrieben wird bei Premiumlagern eine reduzierte dynamische Tragzahl bei der Geometrieschätzung verwendet.

Im Folgenden werden die relevanten Parameter der Lagerinnengeometrie näher beschrieben:

Teilkreisdurchmesser: Bei einem Kugellager enthält der Teilkreis alle Mittelpunkte einer Kugellreihe. Bei einem Rollenlager der Durchmesser des Kreises, der die Rollenachsen in der Mitte der Rollen einer Rollenreihe in einem Lager schneidet. Da die Lagerlaufbahndurchmesser in den Lagerkatalogen nicht angegeben sind, kann der Teilkreisdurchmesser näherungsweise durch den Mittelwert des Innen- und Außenringdurchmessers des Lagers bestimmt werden: D_pw = 0.5(d+D)

Wälzkörperdurchmesser: Bei einem Kugellager der Durchmesser der Kugel. Bei einem Rollenlager wird der Wälzkörperdurchmesser in der Mitte der Rollenlänge bestimmt.

Anzahl der Wälzkörper: Gibt die Anzahl der Wälzkörper in einem Wälzkörpersatz/ in einer Lagerreihe an.

Effektive Rollenlänge: Theoretische maximale Länge der Berührungslinie zwischen einer Rolle und der Laufbahn, in der die Berührungslinie am kürzesten ist. Dies ist üblicherweise entweder der Abstand zwischen den theoretisch scharfen Kanten der Rolle abzüglich der Kantenabstände oder die Laufbahnbreite abzüglich der Schleiffreistiche; es gilt der jeweils kleinere Wert.

Rillenradius der Innen- und Außenringlaufbahn: Die folgende Tabelle gibt die in der FVA-Workbench verwendeten Formeln für die Rillenradien der Innen- und Außenringlaufbahn an und basiert auf der ISO/TS 16281 (DIN 26281):

Mantelradius eines Pendelrollenlagers: Bei einem Pendelrollenlager ist der Wälzkörper kreisförmig ballig ausgeführt. Der Mantelradius entspricht dem Radius dieses Kreises. Nach ISO/TS 16281 (DIN 26281) wird für den Mantelradius R_p= 0.97 r_e verwendet.

Abstand der Lagerreihen: Nur bei zweireihigen Lagern: Gibt den Abstand der Mittelpunkte der Wälzkörper der beiden Reihen an. Bei Pendellagern gilt d_R=D_pw tan(α), sonst wird d_R=0.5 B abgeschätzt.

Lager ohne Lagerringe: Es besteht bei Nadel- und Zylinderrollenlagern die Möglichkeit eine oder beide der Laufflächen ohne Lagerring anzugeben. Bei Katalog-Nadelrollenlagern wird dies automatisch anhand der Katalogbezeichnung berücksichtigt. Dies hat Einfluss auf die Bestimmung der Lagerinnengeometrie. Bei der Berechnung nach FVA 364 wird dies nicht berücksichtigt.

Ausgehend von den Eingangstoleranzen (Lager, Welle und Gehäuse) wird ein Übermaß für die zueinander passenden Teile (Welle - Lager und Lager - Gehäuse) berechnet. Für die Berechnung des effektiven Übermaßes zwischen den Gegenstücken muss der Rauheitsglättungsfaktor berücksichtigt werden. Je höher die Oberflächenrauheit der Gegenstücke ist, desto größer ist der Glättungseffekt, der zu einem Übermaßverlust führt. Der Glättungseffekt der Lager kann vernachlässigt werden, da die Lagerringe gehärtet und präzisionsgeschliffen sind und im Vergleich zur Welle oder zum Gehäuse feinere Oberflächen aufweisen. Im Falle eines Pressitzes auf der Welle kann das effektive Übermaß am Innenring daher wie folgt bestimmt werden

Im Falle einer Presspassung des Außenrings in der Bohrung kann das effektive Übermaß bestimmt werden durch

Der Glättungsfaktor kann vom Nutzer vorgegeben werden. Zusätzlich zu der Übermaßverringerung durch Glättung verringert sich das Übermaß durch ungleichmäßige Wärmeausdehnung. Wenn der Außenring und das Gehäuse oder der Innenring und die Welle aus unterschiedlichen Werkstoffen bestehen, verändert die Betriebstemperaturen das ursprüngliche Übermaß. In der Regel besteht das Lagergehäuse aus einem leichteren Material als der Lageraußenring (höherer Wärmeausdehnungskoeffizient), was zu Übermaßverringerung bei Betriebstemperatur führt. Der Übermaßverringerung aufgrund von Wärmeausdehnung kann wie folgt berechnet werden

wobei d der Fugendurchmesser, α_e, α_i die Wärmeausdehnungskoeffizienten des äußeren und des inneren Materials und ΔT_op die Differenz der Betriebstemperatur zur Referenztemperatur (20°) sind.

Bei einer Presspassung zwischen Welle und Innenring verformt sich die Laufbahn des Innenrings und dehnt sich dadurch aus, was zu einer Verringerung der Lagerluft führt. Ähnlich verhält es sich, wenn eine Presspassung zwischen dem Außenring und der Gehäusebohrung eine Verengung der Außenlaufbahn und damit eine Verringerung der Lagerluft bewirkt. Dieser Effekt ist z.B. in dem Buch "ROLLING BEARING ANALYSIS" von Harris beschrieben und wurde in der FVA 364 III umgesetzt, woher das folgende Bild entnommen ist

Abbildung 26.

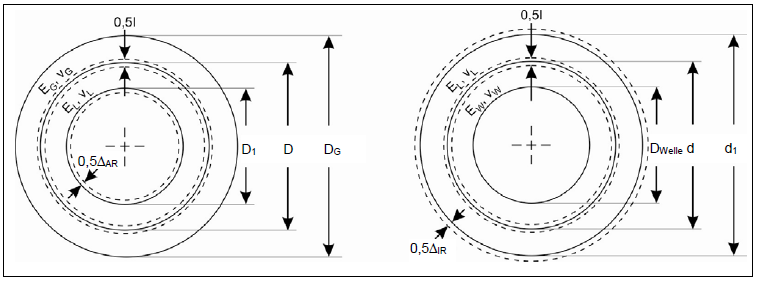
Einschnürung der Außenringlaufbahn (links) und Aufweitung der Innenringlaufbahn (rechts)

Die Berechnung basiert auf der Theorie der elastischen Ringe. Die folgenden Formeln beschreiben die resultierende Spielverminderung:

wobei I das entsprechende wirksame Übermaß ist, D_Welle = innerer Wellendurchmesser, d = Wellenaußendurchmesser/Lagerinnendurchmesser, d₁ = innerer Laufbahndurchmesser, D₁ = äußerer Laufbahndurchmesser, D = äußerer Lagerdurchmesser/Bohrungsdurchmesser, D_G = äquivalenter Gehäuseaußendurchmesser. Ferner sind E_L, ν_L die Werkstoffparameter des Lagers (bzw. der Lagerringe), E_W, ν_W die Werkstoffparameter der Welle und E_G, ν_G die Werkstoffparameter des Gehäuses.

Bei vielen Lagertypen ist es nicht direkt klar, welcher "Laufbahndurchmesser" hier verwendet werden sollte. Die Detaillierte Berechnung verwendet folgende Konvention: Wenn der Wälzkörper in einer Rille der Laufbahn läuft, wird der "Kontaktpunkt" zwischen Wälzkörper und Laufbahn unter dem Nenndruckwinkel verwendet. Die gleiche Überlegung wird für zweireihige Kegelrollenlager mit dem Mittelpunkt der Rolle angestellt. Vernachlässigt man die Lagerluft vor dem Einbau, erhält man:

Bei der detaillierten Berechnung nach FVA 364 werden folgende vereinfachte Formeln zur Bestimmung der Laufbahndurchmesser verwendet:

Hinweis: Bei den meisten Anwendungen wird das Gehäuse kein Hohlzylinder sein, sondern eine beliebig komplexe Konstruktion. Eine gründliche Betrachtung einer solchen komplexen Geometrie erfordert umfangreiche Modellierungs- und Berechnungsdetails. Die FVA-Workbench vereinfacht dies, indem die Angabe des Außendurchmessers eines äquivalenten Hohlzylindergehäuses genutzt wird.

Vereinfachte Berechnung nach FVA 364: Mit dem Schalter vereinfachte Berechnung nach FVA 364 werden die Lagerringe vereinfachend als "steif" angesehen und das ermittelte Übermaß (bzw. die lose Passung) der Ringe wird direkt als Verformung der Laufbahnen berücksichtigt und mit der Lagerluft verrechnet.

Im Betrieb kommt es zu einer ungleichmäßigen Temperaturverteilung im Lager. Nach "Die Wälzlagerpraxis" von Brändlein et. al. ist im Allgemeinen die Temperatur des Innenrings 5-10 K höher als die des Außenrings (wenn das Gehäuse durch Luftstrom gekühlt wird, erhöht sich der Unterschied auf 15-20 K). Der Temperaturunterschied bewirkt, dass sich der Innenring und die Wälzkörper stärker ausdehnen als der Außenring, was zu einer Verringerung der Lagerradialluft führt.

Betrachten wir eine Temperaturdifferenz ΔT_ie zwischen Innen- und Außenring und nehmen an, dass die Temperatur der Wälzkörper in der Mitte liegt. Dann wird reduziert sich das radiale Lagerspiel um

wobei ΔT_ie= Temperaturdifferenz zwischen Innenring und Außenring, α_bearing = 12e-6 mm/K Wärmeausdehnungskoeffizient des Lagers, D_W = Durchmesser des Wälzkörpers, d₁ = Innenlaufbahndurchmesser.

Bei Verwendung der detaillierten Berechnung nach FVA 364 wird die Verringerung des Lagerspiels aufgrund dieser Temperaturdifferenz näherungsweise mit dem mittleren Lagerdurchmesser gemäß SKF Katalog berechnet:

Toleranzklassen geben nur ein Intervall von zulässigen Werten an. Bei der Angabe der Lagertoleranzen kann die entsprechende Kombination von Minimal- und Maximalmaßen zu großen Unterschieden in der Berechnung des Betriebsspiels führen. Aus diesem Grund wird ein mittleres, minimales und maximales Betriebsspiel berechnet. Der Benutzer kann wählen, welche dieser Werte für die anschließenden Steifigkeits- und Lebensdauerberechnungen verwendet werden sollen.

Bei Verwendung der detaillierten Berechnung wird das mittlere Übermaß nach den Erkenntnissen aus FVA 736 I (Wälzlagertoleranzen) als wahrscheinlichstes Übermaß berechnet. Aufgrund von Fertigungsabweichungen ist die Wahrscheinlichkeit groß, dass das Istmaß ein Drittel des Toleranzfeldes von der Bearbeitungsseite her beträgt.

Bei Verwendung der Berechnung nach FVA 364 wird das mittlere Übermaß als arithmetisches Mittel zwischen minimalen und maximalen Übermaß ermittelt.

Im folgenden Abschnitt werden die Formeln für die Umrechnung von Radial- in Axialspiel oder umgekehrt in Abhängigkeit von der Art des Wälzlagers beschrieben.

Rillenkugellager: Die folgenden Beziehungen lassen sich aus der untenstehenden Abbildung ableiten.

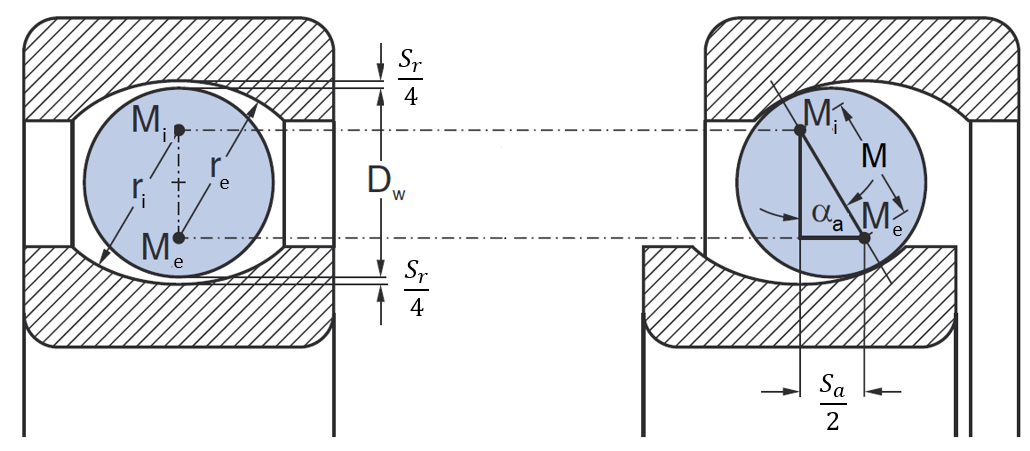
Umrechnung radiales zu axialen Spiel:

Umrechnung axiales zu radialen Spiel:

2-reihiges Schrägkugellager / Vierpunktkugellager / Pendelkugellager / Pendelrollenlager:

Betrachten wir einen Wälzkörper in drei Stellungen, wobei der Außenring fixiert ist. Der Mittelpunkt des Wälzkörpers (oder im Falle eines Pendelrollenlagers der Mittelpunkt des Mantelradius der Rolle) wird mit M_WK bezeichnet, genauer gesagt bezeichnen wir mit M_WK,α eine konzentrische Position, in der der Wälzkörper genau auf dem Teilkreis liegt und Innen- und Außenring den gleichen Abstand zum Wälzkörper haben. Weiterhin bezeichnet M_WK,r die Position, in der der Wälzkörper radial bis zum Kontakt mit der Außenlaufbahn bewegt wurde und M_WK,a die Position, in der der Wälzkörper in axialer Richtung bis zum Kontakt mit der Außenlaufbahn bewegt wurde. Der Abstand zwischen der Mitte der Außenlaufbahnrille M_e und M_WK,r, M_WK,a ist gegeben durch r_e - 0.5 D_W (bzw. durch r_e - R_p für Pendelrollenlager, wobei R_p der Mantelradius der Rolle ist). Für das Pendelrollenlager wird also in den folgenden Formeln der Radius der Rolle (0.5 D_W) durch den Mantelradius (R_p) der Rolle ersetzt.

Umrechnung Axialspiel zu Radialspiel:

Umrechnung Radialspiel zu Axialspiel:

2-reihiges/gepaartes Kegelrollenlager:

Umrechnung Axialspiel zu Radialspiel:

Umrechnung Radialspiel zu Axialspiel:

Die Berechnung der internen Lastverteilung von Radial- und Axialkugellagern basiert auf der ISO/TS 16281:2008 (bzw. DIN 26281:2010) und den Erweiterungen aus FVA 364 und FVA 701. Folgende Einflüsse können berücksichtigt werden:

Position der Wälzkörper in Neutralstellung: Es wird ein rechtshändiges kartesisches u,v,w-Koordinatensystem mit Ursprung im Lagermittelpunkt (halbe Breite, auf der Rotationsachse) eingeführt, dessen Achsen parallel zum Wellen-Koordinatensystem definiert sind, insbesondere entspricht die u-Achse der Rotationsachse. Die radiale Position der Wälzkörper ist durch D_pw festgelegt. Das Betriebsspiel s_α wird zu gleichen Teilen auf Innen- und Außenlaufbahn aufgeteilt. Es gilt also:

Bei einreihigen Lagern liegt der Mittelpunkt der Wälzkörper auf der Radialebene durch den Lagerursprung. Innen- und Außenring (-laufbahn) sind entsprechend der Axialkraftaufnahme der Lagerreihe, dem Druckwinkel und dem Betriebsspiel positioniert. Abhängig von der Axialkraftaufnahme wird der Druckwinkel nun vorzeichenbehaftet definiert: positive Axialkraftaufnahme: α>0, negative Axialkraftaufnahme: α<0. Bei einem Lager in X-Anordnung ist also α₁<0, α₂>0, in O-Anordnung gilt dagegen α₁>0, α₂<0. Für die u-Koordinate der Mittelpunkte der Laufrillenradien gilt dann:

Hinweis: Bei reinen Axiallagern gibt es eine Besonderheit bzgl. des Betriebsspiels. Dieses gibt ja die Beweglichkeit der Lagerringe von einer Grenzstellung zur anderen an. Während das radiale Betriebsspiel noch einmal zwischen einem Wälzkörper "oben" und einem "unten" aufgeteilt wird, wirkt das axiale Betriebsspiel für alle Wälzkörper "voll". Daher wird in obigen Formeln im Allgemeinen 0.25 s_α verwendet. Für α=90° wird dieser Term durch 0.5s ersetzt.

Bei einem zweireihigen Lager sind die Mittelpunkte der Wälzkörper der ersten Lagerreihe um -0.5 d_R axial verschoben, die der zweiten Reihe um +0.5 d_R. Die Werte von u_e, u_i ändern sich dementsprechend auch um -/+ 0.5 d_R . Falls ein Lagerring ovalisiert so ist der Mittelpunkt der entsprechenden Laufbahnkrümmung am Umfangswinkel um den entsprechenden Betrag zusätzlich radial zu verschieben. Das Betriebsspiel etc. wird immer unter der Annahme eines kreisförmigen Lagerrings berücksichtigt.

Hinweis: Ein Vierpunktlager wird durch ein 2-reihiges Schrägkugellager in O-Anordnung modelliert bei dem jeder Wälzkörper "geklont" wird. Bei ausreichender axialer Belastung (Schaeffler: F_a≥1.20F_r , SKF: F_a≥1.27F_r) berühren die Wälzkörper die Innen- und Außenlaufbahn jeweils nur in einem Punkt. In diesem Fall trägt also nur eine der beiden Reihen. Bei Vierpunktkontakt kommt es zu hoher Reibung und damit zu erhöhtem Verschleiß, daher ist dieser Betriebspunkt zu vermeiden. Im mechanischen Modell der FVA-Workbench ist bei Vierpunktkontakt nicht sichergestellt, dass sich die Wälzkörper und ihre Klone in der selben Position befinden. Eine entsprechende Warnung wird ausgegeben.

Hertzscher Kontakt: Für die Berechnung der auf den einzelnen Wälzkörper wirkenden Kräfte kann die Hertz'sche Theorie angewandt werden. Unter der Voraussetzung kleiner Berührungsflächen und einer im Vergleich zu den Körperabmessungen geringen Annäherung der beiden Wälzkörper lassen sich die Oberflächen der Lagerringe und der Kugeln in der Nähe des Berührpunktes als elliptische Paraboloide darstellen. Nach Hertz ergibt sich durch die Kontaktkraft Q über der elliptischen Kontaktfläche mit den Halbachsen a und b die Normaldruckverteilung p(x,y) und die maximale Einfederung δ

wobei Q die Kontaktkraft, E der E-modul, ν die Querkontraktionszahl, Σρ die Krümmungssumme der beiden Körper, κ das Verhältnis der beiden Halbachsen der Hertz'schen Druckellipse und K(κ), E(κ) das vollständige elliptische Integral der 1. Art und 2. Art sind.

Kräftegleichgewicht am Wälzkörper: Unter Berücksichtigung der radial nach außen wirkenden Zentrifugalkraft Q_c ergeben sich unterschiedliche Betriebsdruckwinkel zwischen dem Wälzkörper und der Innen- (α_i) bzw. Außenlaufbahn (\(α_e). Es gilt folgendes Kräftegleichgewicht (vgl. Abschlussbericht FVA 701 III) für die Wälzkörperkräfte an Innen- und Außenlaufbahn Q_i, Q_e:

Die Zentrifugalkraft einer Kugel berechnet sich zu

Hinweis: Reibungseffekte zwischen Wälzkörper und Laufbahn sowie gyroskopische Effekte spielen eine untergeordnete Rolle und werden wie in FVA 701 III vernachlässigt.

Resultierende Lagerkräfte: F_u, F_v, F_w sind die Summen-Kraftkomponenten die von der Welle auf den Innenring wirken. Es gilt (Vorzeichenkonvention von α_i bzw. α_e beachten):

Resultierende Kippmomente: Die zwischen Lagerinnenring und Wälzkörpern wirkenden Kontaktkräfte verursachen Kippmomente um den Lagermittelpunkt falls die Kraftwirkungslinie nicht durch den Mittelpunkt des Lagers geht. Für die Bestimmung des resultierenden Kippmoments aus dem Innen- bzw. Außenringkontakt kann man die jeweilige Kontaktkraft entlang ihrer Wirkungslinie bis in den Mittelpunkt des Wälzkörpers verschieben.

Sei P_WK die aktuelle Position des Wälzkörpermittelpunkts und bezeichne r_P den Abstand zwischen Lagermittelpunkt und dem Wälzkörpermittelpunkt. Definiere das Koordinatensystem u, r, s. Dabei entspricht u der u-Achse des Lagers, r ist der zum Positionswinkel des Wälzkörpers φ gehörige radiale Vektor und s das Kreuzprodukt aus beiden. Sei ψ_WK der Positions-Winkel von P_WK um s ab der r-Achse. Dann ruft die Kraft Q_WK,i die von der Innenlaufbahn auf den Wälzkörper wirkt das Moment M_ψWK um die s-Achse hervor:

wobei der wirksame Tangentialkraftanteil bestimmt wird durch

Die Formeln für das resultierende Kippmoment im Lager lauten schließlich

Hinweis: In DIN 26281 und einigen anderen Publikationen werden diverse Vereinfachungen bei der Kippmomentenberechnung getroffen. Dort wird meist folgende Formel verwendet:

Als Hebelarm wird also der Teilkreisradius verwendet, unabhängig vom genauen Berührpunkt und der Position des Wälzkörpers unter Last. Auch die Tangentialkraft die das Moment hervorruft ist i.A. nicht gleich der Axialkraft.

Die Berechnung der internen Lastverteilung von Radial- und Axialrollenlagern basiert auf der ISO/TS 16281:2008 (bzw. DIN 26281:2010) und den Erweiterungen aus FVA 364 und FVA 701. Folgende Einflüsse können berücksichtigt werden:

Position der Wälzkörper in Neutralstellung: Ausgangspunkt aller Betrachtungen ist der geometrische Mittelpunkt M des Wälzkörpers. Dessen radiale Position ist durch den Teilkreisdurchmesser D_pw gegeben, die axiale Position entspricht der axialen Position der Lagerreihe (=0 beim einreihigen Lager, =0.5 d_R beim zweireihigen Lager). In M hat der Wälzkörper den Durchmesser D_W (gemessen senkrecht zur Rollenachse). Bezeichne mit α_n den Nenndruckwinkel = Druckwinkel am Außenringkontakt und mit ε den halben Kegelwinkel der Rolle (ε=0 wenn kein Kegelrollenlager vorliegt). Dann ergibt sich der Betrag des Druckwinkel am Innenringkontakt zu α_n-2ε und die Rollenlängsachse ist um den Winkel α_n-ε geneigt. Der Mittelpunkt der Lauffläche an Innen- und Außenring sei mit P_i bzw. P_e bezeichnet. Die zugehörigen Durchmesser ergeben sich (unter Berücksichtigung des Betriebsspiel) zu

Analog ergibt sich die axiale Position von P_i bzw. P_e indem man zu der von M den Term sin(|α_n|-ε)( 0.5D_W + 0.25 s_α) verrechnet. Der für die Kontaktberechnung zu verwendende Rollenersatzzylinderdurchmesser ergibt sich zu cos(ε)D_W.

Scheibchenmodell: Bei Rollenlagern lassen sich im allgemeinen die Hertz'schen Gleichungen sowie die Federungsgleichung von Palmgren nicht unmittelbar heranziehen. Die Hertz'schen Gleichungen gelten nur für die Berührung unendlich langer Zylinder. Die Federungsgleichung nach Palmgren berücksichtigt die endlichen Abmaße der Wälzkörper, sie gilt jedoch nur für eine zentrische Belastung der Rolle:

wobei δ die Gesamteinfederung der Rolle und Q die resultierende Kontaktkraft bezeichnet (vergleiche z.B. ISO/TS 16281:2008 oder AB FVA 364 II Abschnitt 2.9.2). Um Effekte wie die Verkippung der Rolle, Profilierung, Bordkontakt, Zentrifugalkraft, etc. berücksichtigen zu können wird üblicherweise das Scheibchenmodell nach ISO/TS 16281 angewendet. Zur Berechnung der Federung wird die Rolle in n_s gleiche Scheiben aufgeteilt, die Zahl der Scheiben muss nach ISO/TS 16281 mindestens n_s = 30 betragen. Für jeden Scheibenkontakt ist die jeweilige Linienlast für den Betriebszustand des Lagers zu bestimmen. Dies erfolgt mit Hilfe der Scheibenverformungen und der Federungsgleichung für die Scheiben nach Palmgren. Bei der Scheibchenmethode wird ein zweidimensionaler Spannungszustand für die einzelnen Scheiben zur Berechnung der Linienlasten angenommen, wodurch Quereinflüsse und damit die Schubspannungen zwischen den Scheiben vernachlässigt werden. Somit werden bei der Scheibchenmethode die einzelnen Scheiben unabhängig von der Einfederung der benachbarten Scheiben zusammengedrückt.

Alternativ zum Federmodell nach ISO/TS 16281 (Palmgren) können die Verformungs-Kraftzusammenhänge aus R. Teutsch and B. Sauer, “An alternative slicing technique to consider pressure concentrations in non-Hertzian contacts", J. Tribol 126(3), 436-442 (2004) verwendet werden. Diese basieren auf einem Regressionsmodell, dass den impliziten Verformungs-Kraftzusammenhang für Linienkontakt der von Dinnik aufgestellt wurde durch eine explizite Formel annähert. Diese Formel berücksichtigt im Gegensatz zu Palmgren explizit die Werkstoffeigenschaften, den Wälzkörperdurchmesser und Teilkreisdurchmessser sowie die Dicke des Außenrings + Gehäusering.

Kräfte- und Momentengleichgewicht am Wälzkörper: Um alle Anwendungsfälle berücksichtigen zu können sind potenziell folgende Einflussfaktoren auf das Kräftegleichgewicht eines Wälzkörpers zu berücksichtigen:

Im axialen und radialen Kräftegleichgewicht gilt für ein Kegelrollenlager

wobei Q_c die Zentrifugalkraft der Rolle und Q_B,i/e die Bordkraft am Innen-/Außenring bezeichnet. Das allgemeine Momentengleichgewicht ergibt sich zu

wobei die Vorzeichen der Exzentrität so vereinbart sind, dass e>0 genau dann wenn die Kraft ein positives (rechtsdrehendes) Moment hervorruft.

Resultierende Lagerkräfte und Kippmomente: Die aus der Belastung der einzelnen Wälzkörper resultierenden Kräfte und Kippmomente werden analog zu dem für die Kugellager beschriebenen Vorgehen ermittelt.

Die Internationale Organisation für Normung (ISO) ist die internationale Vereinigung von Normungsorganisationen (z.B. DIN, ANSI, …). Derzeit sind 164 Länder in der ISO vertreten (121 Vollmitglieder, 39 korrespondierende Mitglieder und 4 Beobachter). Für weitere Informationen zur ISO sei auf die Webseite www.iso.org verwiesen.

Es gibt 249 unterschiedliche Technische Ausschüsse (TC Technical Committees). Das TC 4ist zuständig für Wälzlager und im Unterausschuss (SC Sub Committee) 8 wird die Lagerlebensdauer von Wälzlagern ausgearbeitet. Die ISO 281 wird in der ISO/TC 4/SC 8 erarbeitet dessen Sekretariat vom Deutschen Institut für Normung (www.din.de) gehalten wird. Das zuständige deutsche Gremium ist der Arbeitsausschuss NA 118-01-08 AA „Tragzahlen und Lebensdauer“ im Normenausschuss Wälz- und Gleitlager (NAWGL).

Die Anwendung von Normen ist grundsätzlich freiwillig. Normen sind nicht bindend. Rechtsverbindlichkeit erlangen Normen, wenn Gesetze oder Rechtsverordnungen, z.B. EU-Richtlinien, auf sie verweisen. Daneben können Vertragspartner die Anwendung von Normen auch in Vereinbarungen verbindlich festlegen.

Die aktuelle Version der ISO 281 ist von 2007 und ersetzt die zurückgezogenen Normen ISO 281:1990 , ISO 281:1990/AMD 1:2000 , ISO 281:1990/AMD 2:2000 und ISO/TS 16799:1999. Die aktuelle deutsche Fassung ist die DIN ISO 281:2010-10 und ersetzt die zurückgezogenen Normen DIN ISO 281:1993-01, DIN ISO 281:2009-01, DIN ISO 281/A1:2001-09 und DIN ISO 281/A2:2001-09.

Anwendungsbereich: "Diese Internationale Norm legt Verfahren für die Berechnung der dynamischen Tragzahlen von Wälzlagern in den Größenbereichen fest, die in entsprechenden ISO-Veröffentlichungen angegeben werden, für Lager, die aus heute allgemein verwendetem, hochwertigem, gehärtetem Wälzlagerstahl nach bewährten Herstellverfahren gefertigt sind und deren Wälzkörper und Laufbahnen im Wesentlichen der herkömmlichen Ausführung entsprechen.

Dieses Dokument legt auch Verfahren zur Berechnung der nominellen Lebensdauer fest; dies ist die mit 90 % Erlebenswahrscheinlichkeit erreichbare Lebensdauer, bei heute allgemein verwendetem, hochwertigem Werkstoff, guter Herstellqualität und üblichen Betriebsbedingungen. Zusätzlich legt sie Verfahren zur Berechnung der erweiterten Lebensdauer fest, bei der unterschiedliche Erlebenswahrscheinlichkeiten, Schmierungsbedingung, Schmierstoffverunreinigung und Ermüdungsgrenzbelastung des Laufbahnwerkstoffes berücksichtigt werden.

Der Einfluss von Verschleiß, Korrosion und Elektroerosion auf die Lagerlebensdauer wird in dieser Internationalen Norm nicht behandelt. Dieses Dokument ist nicht auf Konstruktionen anzuwenden, in denen Wälzkörper direkt auf der Welle oder im Gehäuse laufen, es sei denn, die Lauffläche ist in jeder Beziehung der Lauffläche des Lagerringes (oder der Lagerscheibe) gleichwertig, die sie ersetzt. Soweit sich dieses Dokument auf zweireihige Radiallager und zweiseitig wirkende Axiallager bezieht, wird vorausgesetzt, dass diese symmetrisch sind." [DIN ISO 281:2010 Abschnitt 1]

Berechnungsumfang: Zentrale Berechnungsgrößen der ISO 281 sind die

Für die Bestimmung der nominellen Lebensdauer L₁₀ wird die dynamische Tragzahl des Lagers mit der äquivalenten dynamischen Belastung verglichen. Wesentlichen Einfluss auf die Bestimmung der dynamischen Tragzahlen nach ISO 281 haben die Geometriegrößen Anzahl und Durchmesser der Wälzkörper sowie die effektive Rollenlänge bei Rollenlagern. Für die Berechnung nach ISO 281 in der FVA-Workbench werden die von den Lagerherstellern angegebenen Tragzahlen herangezogen. Die äquivalente dynamische Belastung wird in Abhängigkeit der radialen und axialen Lagerkraft bestimmt durch

wobei die Lastfaktoren X,Y in der FVA-Workbench nach den Vorgaben der ISO 281 automatisch ermittelt werden.

Die modifizierte Lagerlebensdauer berücksichtigt den Lebensdauerbeiwert a₁ für die Zuverlässigkeit sowie den Lebensdauerbeiwert a_ISO für die Systembetrachtung:

Der Lebensdauerbeiwert a₁ kann durch die Wahl der zu berücksichtigenden Zuverlässigkeit beeinflusst werden. Der Lebensdauerbeiwert a_ISO wird in Abhängigkeit der Ermüdungsgrenzbelastung C_u, der Verunreinigung (Verunreinigungsbeiwert e_C), der Schmierbedingungen (Viskositätsverhältnis κ) sowie der Lagerbelastung P ermittelt.

Einschränkung: Der Einfluss von Lagerspiel, Verkippung unter allgemeinen Betriebsbedingungen, etc. sind in der ISO 281 nur durch ihren Einfluss auf die wirkenden Lagerkräfte berücksichtigt. Eine genauere Betrachtung der Lagerlebensdauer unter Berücksichtigung der inneren Lastverteilung im Wälzlager ermöglicht die ISO/TS 16281 (DIN 26281).

Geometrieabhängigkeit bei Kugellagern: Auch bei gegebener fester Lagerbelastung (Kräfte) kann sich die Lebensdauer nach ISO 281 durch eine Veränderung der inneren Geometrie ändern. Dies ist auf die geometrieabhängigen Lastfaktoren in ISO 281 zurückzuführen (Tabelle 3). Daher sind die äquivalente dynamische Belastung P und damit auch der Lebensdauerbeiwert a_ISO geometrieabhängig.

Die aktuelle Version der ISO/TS 16281 wurde in 2008 veröffentlicht, ein zugehöriges Corrigendum wurde 2009 herausgegeben. ISO/TS steht für Technische Spezifikation. Diese können erstellt werden, wenn "sich der betreffende Gegenstand noch in der Entwicklung befindet oder wenn aus anderen Gründen die Möglichkeit einer späteren, aber nicht unmittelbaren Einigung über die Veröffentlichung einer Internationalen Norm besteht". Die DIN 26281:2010 ist die deutsche Sprachfassung der ISO/TS 16281 und ersetzt die DIN ISO 281 Beiblatt 4 von 2003.

Anwendungsbereich: "Diese Norm enthält Empfehlungen für die Berechnung der modifizierten Referenz-Lebensdauer unter Berücksichtigung von Schmierung, Verunreinigung und der Ermüdungsgrenzbelastung des Lagermaterials sowie der Schiefstellung oder Verkippung, dem Betriebsspiel des Lagers und der inneren Lastverteilung im Lager. Gegenüber dem in ISO 281 beschriebenen Berechnungsverfahren berücksichtigt das in dieser Norm vorgestellte Berechnungsverfahren zusätzliche Einflussgrößen.

Für die Anwendung dieser Norm gelten die in ISO 281 gegebenen Hinweise und Einschränkungen. Berechnet wird die Ermüdungslebensdauer des Wälzlagers. Andere Schadensmechanismen wie etwa Verschleiß oder Mikropitting (Graufleckigkeit) werden in dieser Norm nicht berücksichtigt.

Diese Norm gilt für einreihige spielbehaftete Radialkugellager unter Radial- und Axiallast und Verkippung. Sie gilt auch für einreihige spielbehaftete Rollenlager unter reiner Radiallast sowie Kantenspannung und Verkippung. Verweise auf Referenzen zu den Methoden zur Berechnung der inneren Lastverteilung unter allgemeinen Belastungsbedingungen sind entsprechend gegeben.

Die Berechnung der internen Lastverteilung und der modifizierten Referenz-Lebensdauer für mehrreihige Lager oder Lager mit einer komplexeren Geometrie kann von den Gleichungen dieser Norm abgeleitet werden. Für diese Lager muss die Lastverteilung für jede Reihe berücksichtigt werden." [DIN 26281:2010]

Umsetzung in der FVA-Workbench: Die erforderliche Erweiterung der Berechnungsmethoden der DIN 26281 auf allgemeine Betriebsbedingungen und komplexere Lagergeometrien erfolgt auf Basis der Projektreihen FVA 364 und FVA 701. Die beinhaltet z.B. die Erweiterung des Verfahrens auf zweireihige Lager oder die exakte Bestimmung der dynamischen Tragzahl einer Scheibe bei Pendel- und Kegelrollenlagern. Auch die Berechnungsmethoden zur Bestimmung der inneren Lastverteilung im Lager erweitern den in der DIN 26281 Umfang deutlich, z.B. durch die Berücksichtigung der Fliehkraft. Details zur Bestimmung der inneren Lastverteilung sind im Abschnitt Steifigkeit dokumentiert.

Die Berechnung der Lebensdauer nach DIN 26281 ist nur bei bekannter Lagerinnengeometrie (Nutzervorgabe, XML-Lager oder Lager aus dem FVA-Lagerkatalog) möglich.

Berechnungsumfang: Neben der detaillierten Bestimmung der inneren Lastverteilung (und damit des Lagerbetriebspunktes/ der resultierenden Lagerkräfte und -momente) sind zentrale Ergebnisgrößen der DIN 26281 die

Wesentlicher Unterschied zur Berechnung nach ISO 281 ist, dass zur Bestimmung der Lebensdauer die Belastung und Tragfähigkeit der einzelnen Wälzkörperkontakte herangezogen wird. Im Falle eines Kugellagers wird dazu die dynamische Tragzahl des Einzelkontakts für Innen- und Außenring mit Hilfe der Geometriegrößen aus der Tragzahl des Lagers ermittelt. Dem Gegenüber steht die dynamisch äquivalente Belastung des Innen- und Außenringkontaktes die aus den wirkenden Wälzkörperkräften ermittelt wird. Beim Rollenlager wird die dynamische Tragzahl einer Scheibe der Rolle am Innen- und Außenring auf Basis der Tragzahl des Lagers und der Geometriegrößen bestimmt. Diese wird dann zur dynamisch äquivalenten Belastung einer Scheibe am Innen- und Außenring in Bezug gesetzt. Die dynamisch äquivalente Referenzbelastung des Lagers ergibt sich schließlich aus der Tragzahl des Lagers und der berechneten nominellen Referenz-Lebensdauer. Für die Bestimmung der modifizierten (erweiterten) Referenz-Lebensdauer werden der Lebensdauerbeiwert a₁ für die Zuverlässigkeit sowie der Lebensdauerbeiwert a_ISO mit herangezogen. Diese werden nach den Vorgaben der ISO 281 ermittelt, allerdings wird für die Bestimmung von a_ISO die dynamisch äquivalente Referenzbelastung (Kugellager) bzw. die dynamisch äquivalente Belastung der Lagerscheibe (Rollenlager) berücksichtigt.

Bestimmung der Lastverteilung und Pressung bei Rollenlagern: Wie im Abschnitt Rollenlagersteifigkeit bereits beschrieben werden bei der Scheibchenmethode die Quereinflüsse zwischen den Scheiben vernachlässigt und die Einfederung einer Scheibe hat keinen Einfluss auf die benachbarten Scheiben. Daher können mit dieser Methode insbesondere ggfs. auftretende Kantenpressungen (aufgrund zu geringer Profilierung/ zu hoher Verkippung) nicht ermittelt werden.

Die DIN 26281 bietet die Möglichkeit als einfache Näherung die mit der Scheibenmethode ermittelte Lastverteilung durch die empirische Lastüberhöhungsfunktion nach Gleichung (60) der DIN 26281 (2010) zu korrigieren um den Effekt des Schubspannungseinfluss und der ggfs. daraus resultierenden Kantenspannungen zu berücksichtigen. Diese Näherung ist nur anwendbar für das Näherungsprofil nach DIN 26281 und unter den Voraussetzungen mittlerer Belastung und Verkippung des Lagers von weniger als 4 Winkelminuten. Für die allgemeine Berechnung wird ein höherwertiges Verfahren empfohlen.

Alternativ kann eine Berechnungsmethode verwendet werden die den Schubspannungseinfluss der Scheiben mit berücksichtigt. Damit lassen sich für beliebige Rollenprofile Kanteneffekte berechnen und bei der Lebensdauerberechnung berücksichtigen. Dabei wird der Einfluss der Belastung einer Scheibe auf die Verformung der benachbarten Scheiben mit berücksichtigt. Die aktuelle Lagerberechnung der FVA-Workbench verwendet dabei die Einflusskoeffizientenmatrix aus R. Teutsch and B. Sauer, “An alternative slicing technique to consider pressure concentrations in non-Hertzian contacts", J. Tribol 126(3), 436-442 (2004). Die Lagerberechnung nach FVA 364 verwendet die Methode nach H. Reusner, "Druckflächenbelastung und Oberflächenverschiebung im Wälzkontakt von Rotationskörpern", Dissertation, Karlsruhe University, 1977