Kegelradberechnung
Für Kegel- und Hypoidradsätze stehen in der FVA-Workbench eine Vielzahl an Berechnungsmöglichkeiten mit sehr unterschiedlicher Komplexität und Einsatzmöglichkeiten zur Verfügung. Dazu gehören Auslegungsberechnungen, auf Grundgeometriedaten beruhende Tragfähigkeits- bzw. Sicherheitsnachweise sowie örtliche Berechnungsverfahren unter Verwendung der Herstellungssimulation oder einer exakten Mikrogeometriebeschreibung als 3D-Zahnoberfläche.
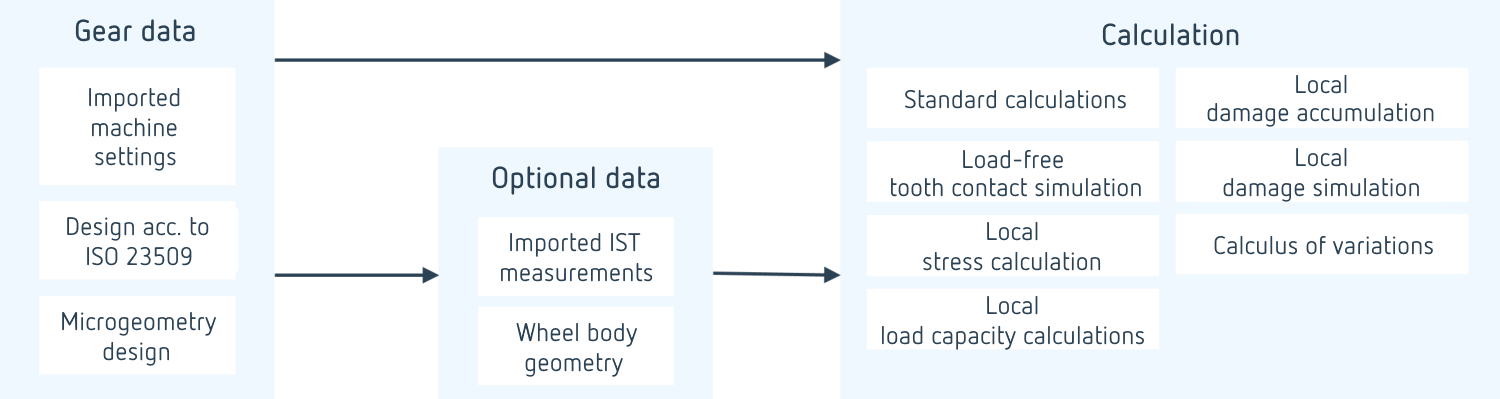
Je nachdem, wie detailliert die Kegelradgeometrie beschrieben ist, stehen verschiedene Berechnungsmöglichketen zur Verfügung.
 Kegelradsatz | 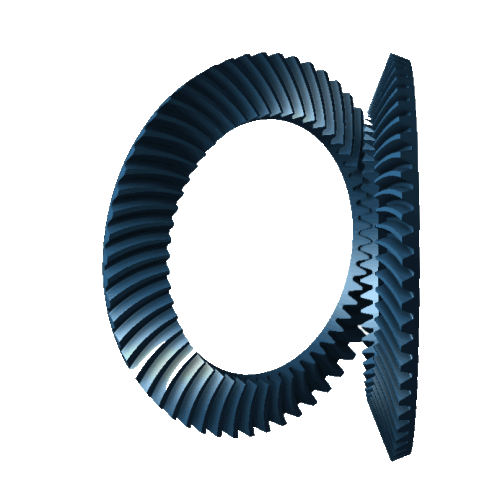 Kegelradsatz mit Achswinkel > 90° |  Hypoidradsatz |  Hypoidradsatz mit Achswinkel < 90° |  Geradverzahnung |
Geometrie
Geometrieauslegung nach ISO 23509
Als Bindeglied zwischen den auf der Grundgeometrie beruhenden Normverfahren und den erweiterten örtlichen Berechnungen kann die Geometrieauslegung nach ISO 23509 verwendet werden. Wurde das Getriebemodell mit der Getriebevorauslegung in der FVA-Workbench erstellt, so enthalten bereits alle für die Kegelradstufe notwendigen Attribute Vorschlagswerte, um die Geometrieauslegung nach ISO 23509 auszuführen.
Mit dem Ergebnis dieser Auslegungsberechnung, der internen Schnittstellendatei standard.kgd, können die Eingriffsverhältnisse der Zahnpaarung berechnet und über eine Anpassung der Mikrogeometrie praxisrelevant gestaltet werden.
Die örtlichen Berechnungen können damit das reale Tragfähigkeitsverhalten näherungsweise abbilden. Es werden so entscheidende Faktoren, z.B. Mikrogeometrie, Verformung und Relativlageveränderung unter Last) berücksichtigt, die bei einer Normberechnung geringen oder keinen Einfluss haben.
Import von Kegelradgeometrie
Für die geometrische Beschreibung der Kegelradverzahnung einschließlich der Mikrogeometie stehen folgende Eingabewege zur Verfügung:
Import von Maschineneinstelldaten für die üblichen Firmenschnittstellen (Grundgeometrie sowie vollständige Maschineneinstelldaten) über eine Standard.kgd Datei.
Import einer freien 3D-Kegelradgeometrie gemäß der KIMoS-3D-Neutraldaten und der dazugehörenden Grundgeometriedaten.
Eingabe von Grundgeometriedaten nach ISO23509 (Berechnung und Import der Maschineneinstelldaten erfolgt intern)
Nach dem erfolgreichen Import mittels einer der drei oben beschriebenen Eingabewege stehen die Daten der Kegel- bzw. Hypoidverzahnung sowohl für alle lokalen Verzahnungsberechnungen als auch für die Tragfähigkeitsberechnung nach Normen und Klassifikationsgesellschaften zur Verfügung.
Um die Konsistenz der Daten mit den Maschineneinstelldaten zu sichern, werden die Geometrieattribute im Editor gesperrt und eine manuelle Eingabe ist nicht mehr möglich.
Für Tragfähigkeitsberechnungen nach Normen und Klassifikationsgesellschaften ist alternativ zu den drei Eingabewegen die Eingabe der Grundgeometriedaten, z.B. aus Zeichnungen oder Dimensionierungsblättern, in den Editor „Hauptgeometrie“ möglich. Lokale Verzahnungsberechnungen können dann aber aufgrund der fehlenden Mikrogeometrie nicht freigegeben werden. Die zur Verfügung stehenden Berechnungsverfahren sind in den Abschnitten Normtragfähigkeit und Klassifizierer zusammengestellt.
Import von Messdaten
Für die Durchführung der örtlichen Beanspruchungs- und Tragfähigkeitsberechnungen ist die Kenntnis der exakten Flankengeometrie notwendig. Über den Messdatenimport in der FVA-Workbench können Ist-Messdaten von Kegelrädern für die Nutzung in der Zahnkontaktanalyse eingelesen und aufgearbeitet werden. Dabei werden Messausreißer aus den Istmessdaten entfernt und Flankenabweichungen (fcb, fcp, fv, fHb, fHa) zwischen der Soll- und der durch die Messdaten repräsentierten Ist-Geometrie berechnet.
Hinweis
Im Tutorial Kegelrad-Messdatenverarbeitung wird der Import von Messdaten in der FVA-Workbench gezeigt.
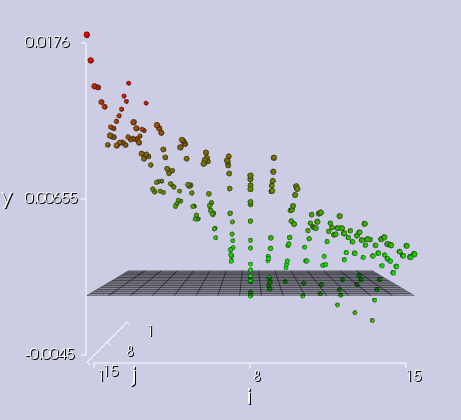
Im Messdaten-Importwizard können Messreißer in den Istmessdaten interaktiv selektiert und entfernt werden.
Die Zahnkontaktanalyse auf Basis von 3D-Messdaten kann auf die folgenden zwei Arten erfolgen:
Indirekte Nutzung durch Berücksichtigung von Flankenabweichungen
Direkte Nutzung durch Berücksichtigung von Flankenabweichungen und zusätzliche Verwendung der Ist-Messdaten zur Generierung der Ausgleichsflächen
Ausgleichsflächen
Die Grundlage jeder örtlichen Berechnung bildet eine möglichst exakte mathematische Darstellung der Zahnflankengeometrie (inklusive der Mikrogeometrie). Das erfolgt über Ausgleichsflächen, da diese einen schnellen Zugriff auf jeden beliebigen Flankenpunkt garantieren. Um die Qualität dieser Ausgleichsflächen beurteilen zu können, stehen für die Flanken- und Fußbereiche Diagramme zur Verfügung, die die Abweichungen der Ist-Geometrie (berechnete Ausgleichsflächen) von der Soll-Geometrie (berechnete Punkte aus der Herstellungssimulation bzw. Eingelesene 3D-Geometrie) darstellen. Die maximale absolute Abweichung wird im Diagramm ausgewiesen und markiert. Die Abdeckung der Nutzflanke durch Berechnungspunkte bzw. die Lage der Punkte aus dem 3D-Daten-Import werden so überprüfbar.
Mathematische Beschreibung der Zahnoberfläche
Zur mathematischen Beschreibung der Zahnflanken- und Zahnfußbereiche für die lokalen Berechnungen stehen alternativ zu den Bezier-Flächen nun auch NURBS-Flächen zur Verfügung. Die NURBS-Flächen werden über die Vorgabe von Polynomgrad und Anzahl der Kontrollpunkte konfiguriert. Vorteile bietet der NURBS-Flächenansatz vor allem für Verzahnungen mit Rücknahmen (Kopfrücknahme, Endrücknahme, Protuberanz), für geschmiedete Differentiale (komplexe Fußgeometrie charakterisiert durch starke Änderungen im Zehen- und Fersenbereich) und zum Nachrechnen von Verzahnungsschäden, die über 3D-Messdaten angegeben werden.
Tragfähigkeitsberechnung
Normtragfähigkeit
Für die Berechnungsverfahren nach Norm sind als Eingabegrößen lediglich die Makrogeometrie der Kegelradverzahnung, die Betriebsbedingungen, bestehend aus Drehzahl, Drehmoment und Betriebsart, sowie Werkstoff- und Schmierstoffangaben erforderlich. Grundlage dieser Tragfähigkeitsnachweise bildet eine geeignete Umrechnung der Kegelradgeometrie auf eine Ersatz-Stirnradverzahnung, die die Eingriffsverhältnisse der zu berechnenden Kegelradverzahnung näherungsweise nachbildet. Als Ergebnis werden Sicherheitsfaktoren geliefert, die Aussagen über die Tragfähigkeit der Verzahnung bei der vorgegebenen Belastung ermöglichen. Folgende Berechnungen können zur Nachrechnung von Hypoidverzahnungen sowie von nicht-achsversetzten Kegelradverzahnungen herangezogen werden:
Ermittlung der Ersatz-Stirnradverzahnung von Kegelrad- und Hypoidverzahnungen nach verschiedenen Verfahren
Tragfähigkeitsberechnung nach ISO 10300 (Ausgabe 2014)
Tragfähigkeitsberechnung nach FVA 411 (2008)
Tragfähigkeitsberechnung nach Niemann/Winter (1986)
Tragfähigkeitsberechnung nach Niemann Band 2 (1965)
Berechnung der Flankenbruchgefährdung nach FVA 240-II
Flankenbruchgefährdung nach Witzig /Boiadjev aus FVA 556 III
Graufleckentragfähigkeit nach FVA 516 (2011)
Fresstragfähigkeit nach FVA 519 (2013)
Fresstragfähigkeit nach ISO/TS 6336-20 -> Nachfolgedokument für ISO/TR 13989-1 (Ausgabe 2000)
Fresstragfähigkeit nach ISO/TS 6336-21 -> Nachfolgedokument für ISO/TR 13989-2 (Ausgabe 2000)
Berechnung des Wirkungsgrads und der Verlustleistung nach Wech (1987)
Berechnung und Ausgabe der Verzahnungskräfte
Berücksichtigung der Toleranzen nach ISO 17485 (Ausgabe 2006) für Verlagerungen und Abweichungen
Für die Nachrechnung von nicht-achsversetzten Kegelradgetrieben sind zusätzlich folgende Berechnungsvorschriften uneingeschränkt gültig:
Tragfähigkeitsberechnungen nach ISO 10300 (2001)
Tragfähigkeitsberechnungen nach DIN 3991
Verschleißberechnung nach Niemann/ Winter
Lastkollektivberechnungen mit Einstufen-Lastkollektiven sind bei der Tragfähigkeitsberechnung nach DIN 3991, ISO 10300 (2014), AGMA-C10 und FVA 411 integriert und können optional bei der Gesamtsystem- und Einzelkomponentenberechnung aktiviert werden.
Klassifizierer
Zusätzlich zu den Normberechnungsverfahren können die Rules der Marineklassifikationsgesellschaften und der AGMA berechnet werden. Um die Berechnung durchzuführen, sind die Makrogeometriegrößen der Kegelradverzahnung, die Betriebsbedingungen sowie Werkstoff- und Schmierstoffangaben erforderlich. Die folgenden aktuellen Berechnungsmethoden sind verfügbar:
Tragfähigkeit nach AGMA 2003-C10
Tragfähigkeit nach American Bureau of Shipping 2016
Tragfähigkeit nach Bureau Veritas 2014
Tragfähigkeit nach Det Norske Veritas / Germanischer Lloyd 2015
Tragfähigkeit nach Lloyd’s Register 2015
Tragfähigkeit nach China Classification Society 2015
Tragfähigkeit nach Russian Maritime Register of Shipping 2017
Zudem stehen die folgenden Berechnungsmethoden vorangegangener Ausgaben zur Verfügung:
Tragfähigkeit nach AGMA 2003-B97
Tragfähigkeit nach AGMA 2003-A86
Tragfähigkeit nach Det Norske Veritas 2003
Tragfähigkeit nach Det Norske Veritas 1993
Tragfähigkeit nach Germanischer Lloyd 1998
Tragfähigkeit nach Lloyd’s Register 1998
Erweiterte Verzahnungsberechnung
Bei der erweiterten Verzahnungsberechnung werden die komplexen Kontaktbedingungen realitätsnah nachgebildet. Sie basiert auf der lastfreien Zahnkontaktsimulation. Dabei werden die im Eingriff befindlichen Nutzflanken in die erwartete Relativlage gebracht und aufeinander abgewälzt.
Die dafür notwendige Sollgeometrie der Verzahnung wird über eine Fertigungssimulation ermittelt oder als freie 3D-Kegelradgeometrie vorgegeben (siehe Import von Kegelradgeometrie). Alle für eine Fertigungssimulation notwendigen Daten, z.B. Grundgeometrie, Maschineneinstelldaten, Werkzeugdaten und Kinematik einschließlich Zusatzbewegungen, werden beim Import der Kegelradgeometrie aus herstellerspezifischen Schnittstellen (z. B. KIMoS-Neutraldaten) übernommen und auf die universelle Kegelradverzahnmaschine umgerechnet. Die Zahnflanken, einschließlich des Zahnfußbereiches, werden punktweise simuliert und bilden die Sollgeometrie der Verzahnung ab.
Aus den Sollgeometriedaten berechnete Ausgleichsflächen gestatten nun, die Zahnflanken sowie den Fußbereich mathematisch geschlossen darzustellen. Mit Hilfe dieser Ausgleichsflächen lässt sich außerdem eine gute Näherung für die Krümmungsverhältnisse auf den Zahnflanken bestimmen.
Aufbauend auf den Ergebnissen der lastfreien Zahnkontaktsimulation folgt zunächst die lokale Beanspruchungsberechnung und anschließend die Berechnung lokaler Tragfähigkeiten und Sicherheiten.
Lastfreie Zahnkontaktsimulation
Bei der lastfreien Zahnkontaktsimulation werden die mit Ausgleichsfächen beschriebenen und im Eingriff befindliche Zahnflanken aufeinander abgewälzt. Im Zugbetrieb ist definitionsgemäß die konkave Ritzel- mit der konvexen Tellerradflanke im Eingriff und im Schubbetrieb die konvexe Ritzel- mit der konkaven Tellerradflanke.
Die lastfreie Zahnkontaktsimulation liefert unter Beachtung der vorgegebenen oder im Gesamtsystem berechneten Relativlage von Ritzel und Tellerrad zueinander folgende Ergebnisse:
Ease-Off
In der Ease-Off-Darstellung werden die Abweichungen beim Abwälzen im theoretischen (nicht korrigierten) Wälzverhältnis auf der Projektion der Tellerradflanke in die Axialschnittebene aufgetragen. Hieraus lassen sich Aussagen zur Wirksamkeit der Mikrogeometrieauslegung ableiten.
Lastfreies Tragbild
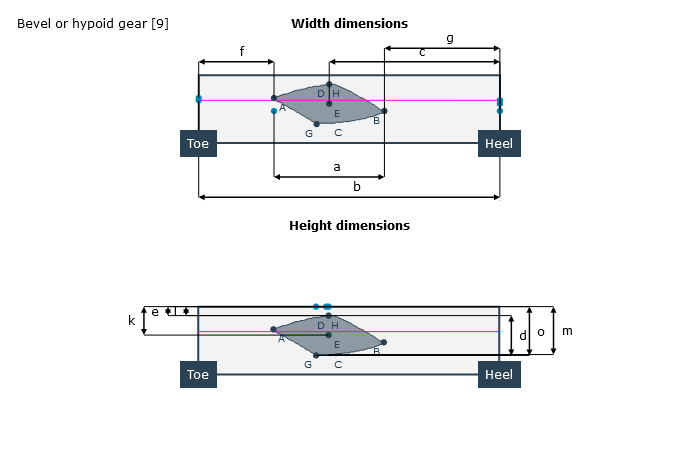
In der Tragbilddarstellung wird die Größe und Lage des lastfreien Tragbildes mit einer Tuschierdicke von 6 µm auf der Projektion der Ritzel- sowie Tellerradflanke in die Axialschnittebene dargestellt. Dabei werden ggf. vorhandene Eingriffsstörungen (Eingriff des Zahnkopfes in den Zahnfußbereich des Gegenrades) auf der Nutzflanke rot markiert. Zusätzlich wird das Kopfgrundspiel im Fußgrund eingetragen.
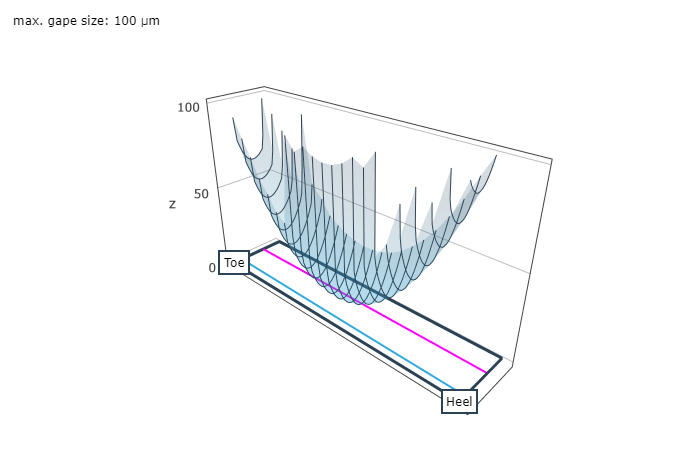
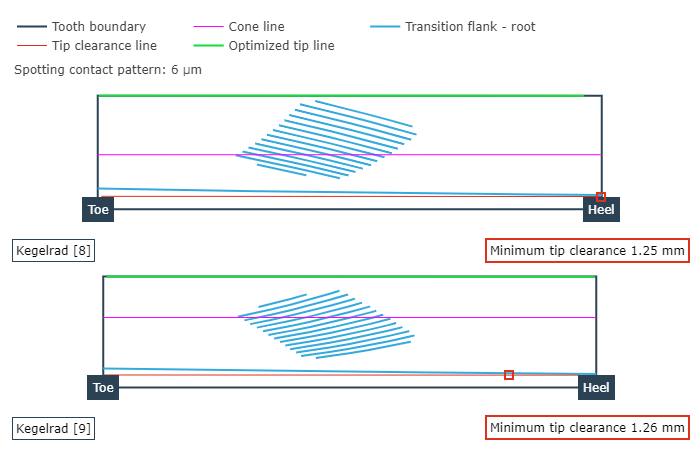
Ease-Off-Darstellung über der Tellerradflanke (links) und Lastfreies Tragbild von Rad und Ritzel (rechts).
Optional können noch folgende weitere Ergebnisse berechnet werden:
Verdrehflankenspiel
Da Kegelräder in der Praxis immer Flankenmodifikationen besitzen, ist das Verdrehflankenspiel über den Eingriffsstellungen betrachtet nicht konstant. Die Differenz zwischen minimalem und maximalem Verdrehflankenspiel entsteht durch eine Überlagerung der Wälzabweichungen von Schub- und Zugbetrieb. Ein zu geringes Verdrehflankenspiel kann durch die unter Last zu erwartenden Relativlageänderungen zum Klemmen führen. Ein zu großes Flankenspiel kann zu erhöhten Laufgeräuschen und verminderter Tragfähigkeit führen. Bei der Berechnung des Verdrehflankenspiels werden die Mikrogeometrie, die Einbaulage sowie die Relativlageänderungen unter Last berücksichtigt.
Ziehbarkeit (Montierbarkeit) des Kegelritzels
Die Ziehbarkeit wird ausgehend von der Solleinbaulage und optional unter Vorgabe einer Tellerradabsenkung ermittelt.
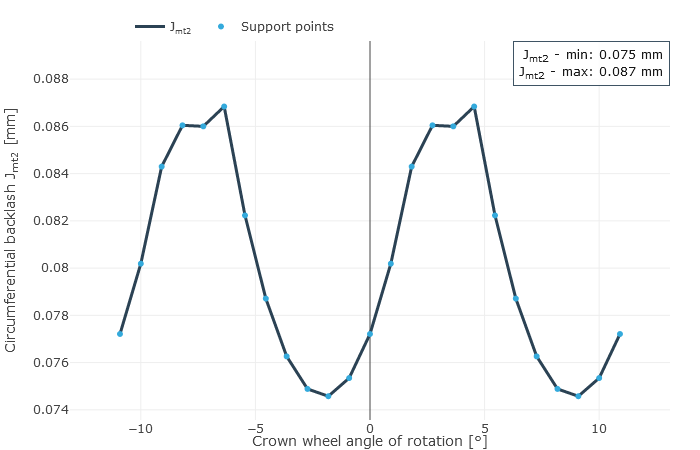
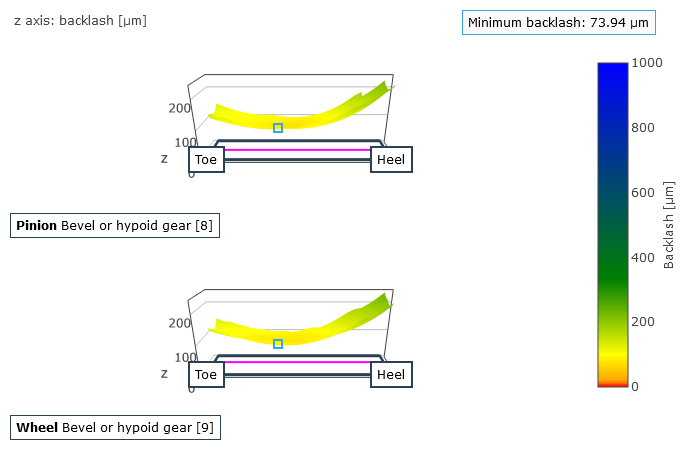
Mittleres Verdrehflankenspiel über dem Tellerraddrehwinkel (links) und Rückflankenspiel: Spalt zwischen den Gegenflanken (rechts).
Die Ergebnisse der lastfreien Zahnkontaktsimulation bilden die Grundlage für alle nachfolgenden, weitergehenden Berechnungen.
Ziehbarkeit des Kegelritzels
Ein Ritzel ist ziehbar, wenn es aus dem Eingriff herausgedreht werden kann und sich das Ritzel nur entlang der Radachse bewegt. Die Relativlage der Radachse des Ritzels verändert sich folglich nur in axialer Richtung aus dem Eingriff heraus. Ziehbarkeit beschreibt sowohl den Montage- sowie den Demontagevorgang. Dies hat einen enormen Einfluss, insbesondere auf die Gehäusegestaltung. Die Tatsache, ob axiale Ziehbarkeit des Kegelritzels vorliegt oder nicht, beeinflusst die Montage- und Demontagevorgänge erheblich.
Als Ergebnis der Ziehbarkeitsberechnung wird das minimale und maximale Verdrehflankenspiel über der axialen Ritzelverschiebung grafisch dargestellt. Dabei können folgende drei Fälle auftreten:
Ziehbarkeit
Die Kurven des minimalen und maximalen Verdrehflankenspiel sind monoton steigend. Die Minima liegen im Koordinatenursprung.
Bedingte Ziehbarkeit
Das Minimum des minimalen Verdrehflankenspiel ist negativ und das Minimum des maximalen Verdrehflankenspiel ist positiv. Das bedeutet, in den entsprechenden axialen Ritzelpositionen gibt es Eingriffsstellungen, in denen sich Ritzel und Tellerrad nicht durchdringen. Nur unter idealen Bedingungen kann durch Verdrehen von Ritzel und Tellerrad zueinander, während der axialen Ritzelverschiebung, ein Klemmen verhindert werden. Ohne nähere Prüfung ist keine Ziehbarkeit anzunehmen.
Keine Ziehbarkeit
Die Minima sind negativ, d.h. für alle axialen Ritzelpositionen mit negativem minimalen und maximalen Verdrehflankenspiel wird in allen Eingriffsstellungen eine Durchdringung berechnet. Die Verzahnung klemmt und das Ritzel kann nicht axial bewegt werden.
Messer-kopfradius | Ziehbarkeit ohne Tellerradabsenkung | Ziehbarkeit nach Tellerradabsenkung |
|---|---|---|
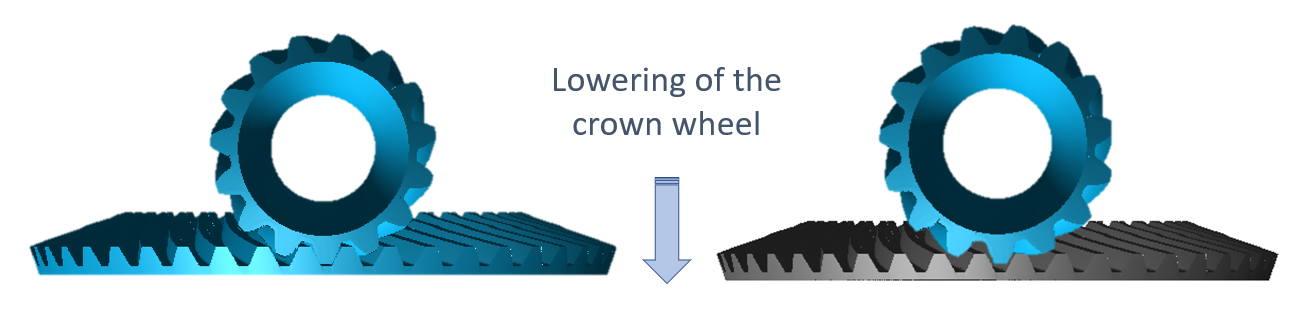 | ||
rco = 55mm | 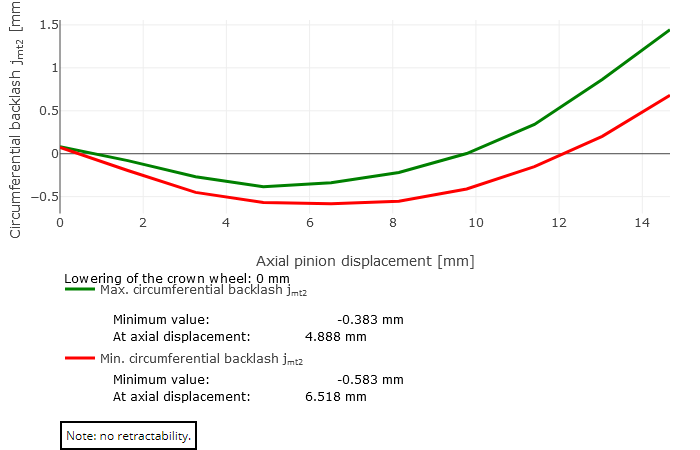 Fall 3: Keine Ziehbarkeit | 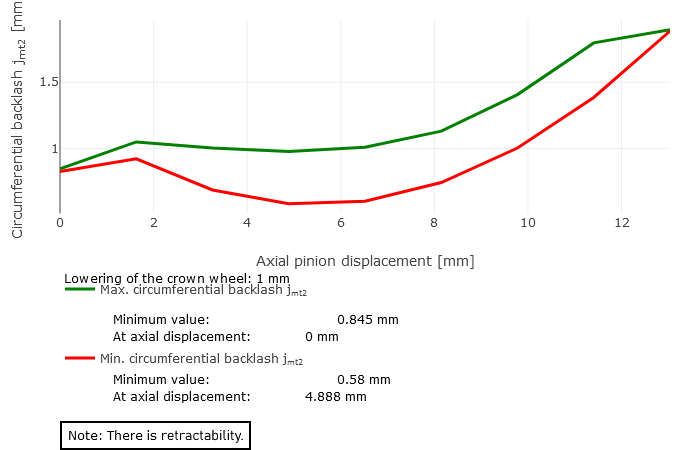 Fall 1: Ziehbarkeit vorhanden (Tellerradabsenkung = 1mm) |
rco = 62mm | 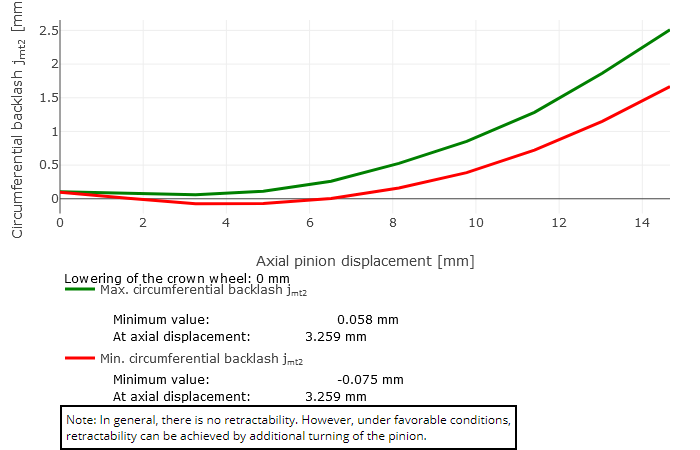 Fall 2: Bedingte Ziehbarkeit | 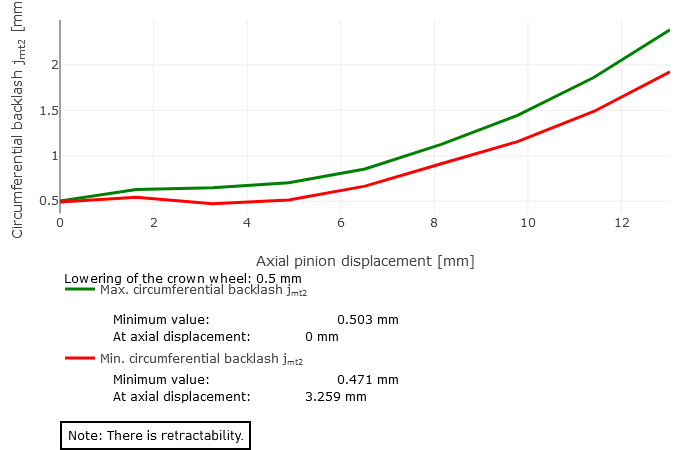 Fall 1: Ziehbarkeit vorhanden (Tellerradabsenkung = 0,5mm) |
rco = 75mm | 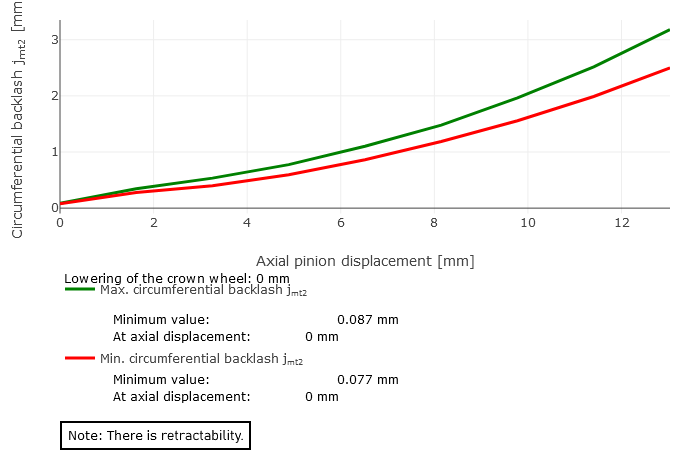 Fall 1: Ziehbarkeit vorhanden | |
Örtliche Beanspruchungsrechnung
Aufbauend auf den Ergebnissen der lastfreien Zahnkontaktsimulation erfolgt die örtliche Beanspruchungsberechnung auf Grundlage der Einflusszahlenmethode - einem numerischen Berechnungsverfahren, mit dem Last- und Spannungsverteilungen an diskreten Stellen effizient berechnet werden können.
Für die Berechnung der Zahnsteifigkeit können je nach Berechnungs- und Modellumfang folgende Verfahren verwendet werden:
BEM-Einflusszahlen-Methode
Kombination aus BEM-Einflusszahlen und FEM-Einflusszahlen für den Radkörper
FEM-Einflusszahlen-Methode
Standardmäßig wird die Steifigkeit des Radkörpers durch einen elastischen Halbraum angenähert. Mit der FVA-Workbench ist es optional möglich, explizit einen Radkörper und dessen Einspannung als komplexe Radkörpergeometrie vorzugeben. Radkörper können einfach als CAD-Geometrie geladen, positioniert und in der FVA-Workbench vernetzt werden. Die Berechnung der Einflusszahlen erfolgt dann unter Berücksichtigung des vorgegebenen Radkörpers nach FVA 223 XVI (Forschungsvorhaben „BECAL-Radkörper“, IMM der TU Dresden, Prof. Dr. Berthold Schlecht). Die Verformungs- und Spannungsberechnung an Kegel- und Hypoidrädern kann auch mithilfe der FEM durchgeführt werden. Dies ermöglicht die Berechnung der 3D Zahnfußtragfähigkeit. Durch die detailliertere Berechnung der dreidimensionalen Verformung kann zudem das Betriebsflankenspiel an der Rückflanke berechnet und ausgewertet werden.
Die Berechnung der Zahnverformung und der Zahnfußspannungen erfolgt unter Verwendung der vorliegenden Sollgeometrie, die aus der Herstellungssimulation ermittelt oder über die 3D-Solldaten importiert wurde. Aus den Ausgleichsflächen, die Flanken- und Fußbereiche beschreiben, werden mehrere Normalschnitte entlang der Zahnbreite ermittelt, die dann jeweils den realen Zahn- und Fußbereich sowie dessen Änderung über der Zahnbreite beschreiben. Mittels der Boundary-Element-Methode (BEM) werden auf Basis dieser Normalschnitte die Zahnverformung und Zahnfußspannungen berechnet (siehe FVA 223 XI, Forschungsvorhaben „BECAL – Belastungs- und Beanspruchungsmodell“, IMM der TU Dresden, Prof. Dr. Berthold Schlecht).
Als Ergebnis erhält der Anwender örtlich aufgelöst die Last- und Pressungsverteilung sowie die lokalen Gleitgeschwindigkeiten. Daraus wird ein resultierender Wirkungsgrad für die betrachtete Stufe und aus der berechneten Geometrie und der Kontaktbeschreibung der Verzahnungssteifigkeitsverlauf über den Eingriffsstellungen und die Wälzabweichung bestimmt. Die Wälzabweichungen sind ein Maß für das Laufverhalten der Verzahnung in einem Betriebspunkt. Die maximalen Fußspannungen über alle Eingriffsstellungen werden über der Zahnbreite dargestellt.
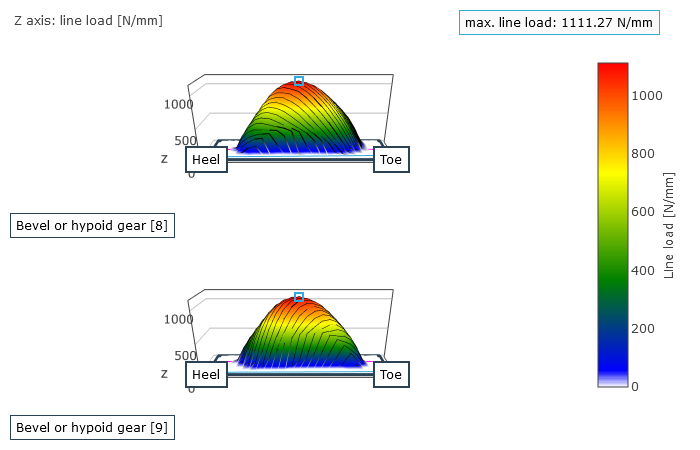
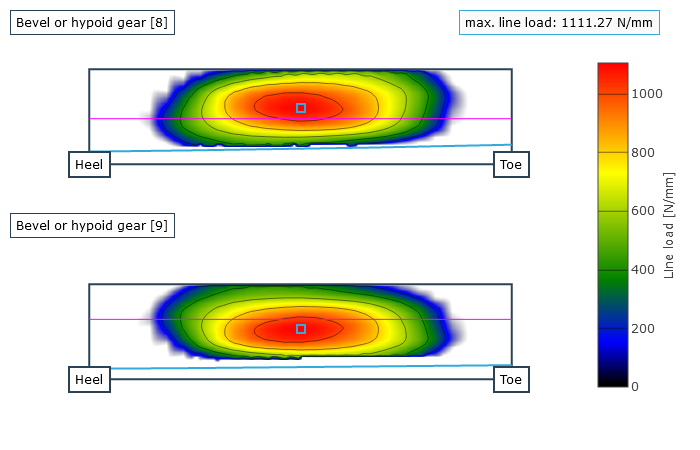
Darstellung der Lastverteilung auf der Flanke
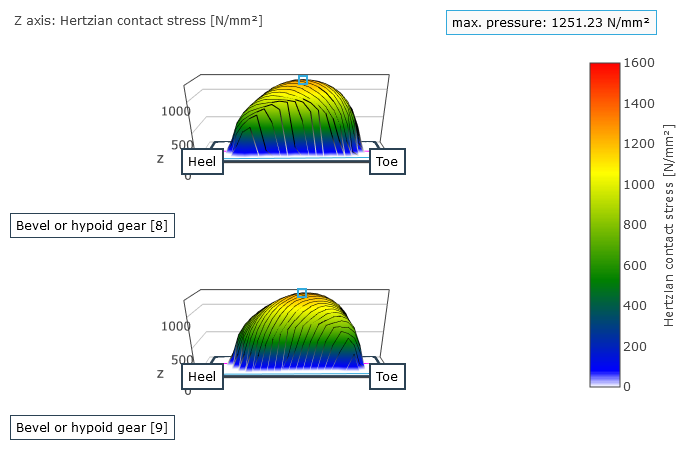
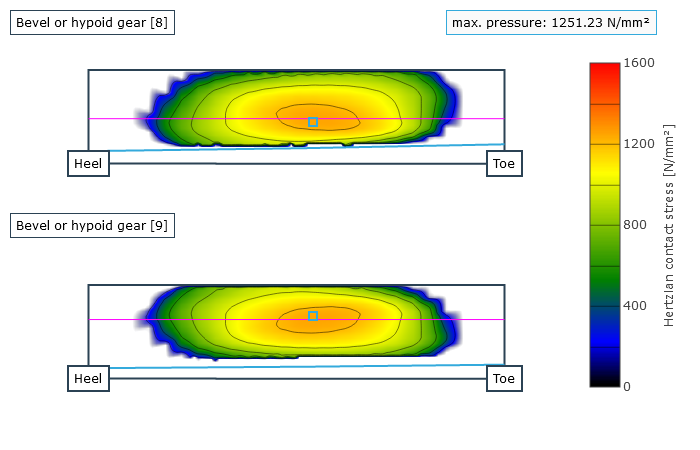
Darstellung der Pressungsverteilung auf der Flanke
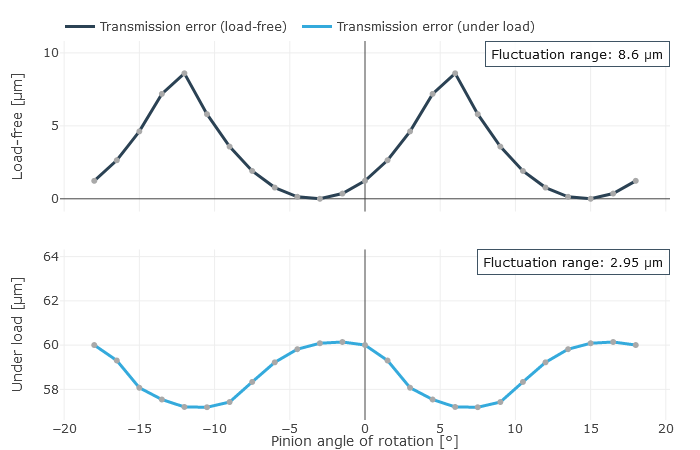 Drehwegabweichung | 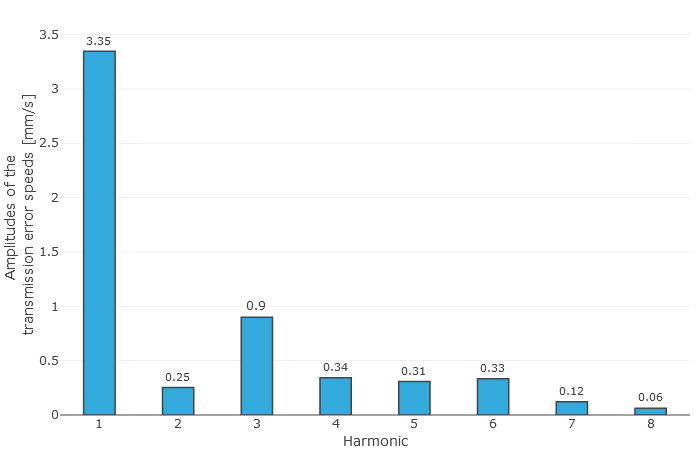 Spektrum der Drehwegabweichung |
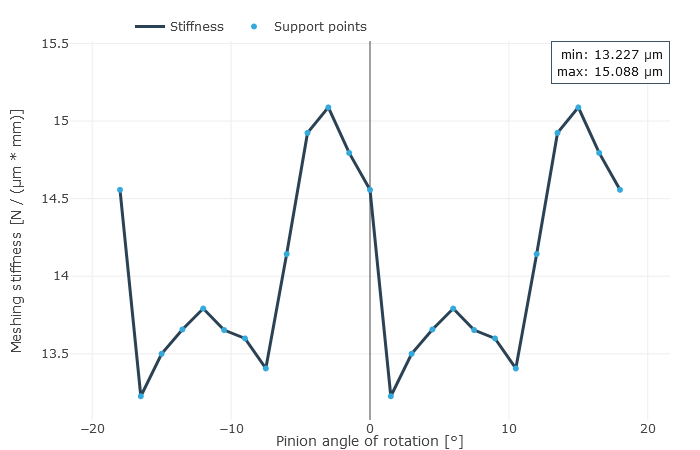
Verzahnungssteifigkeit
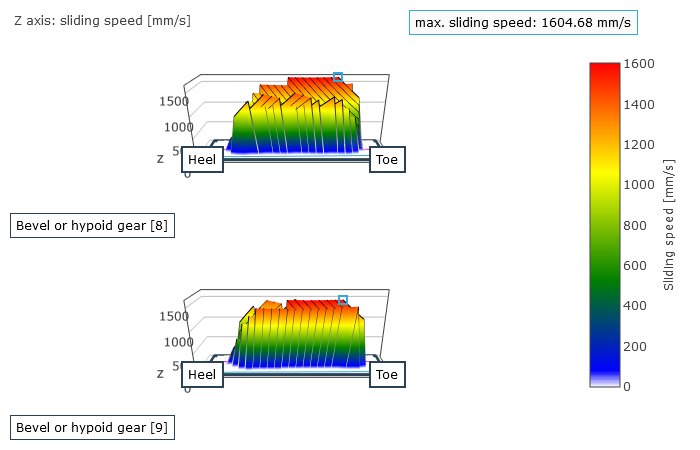
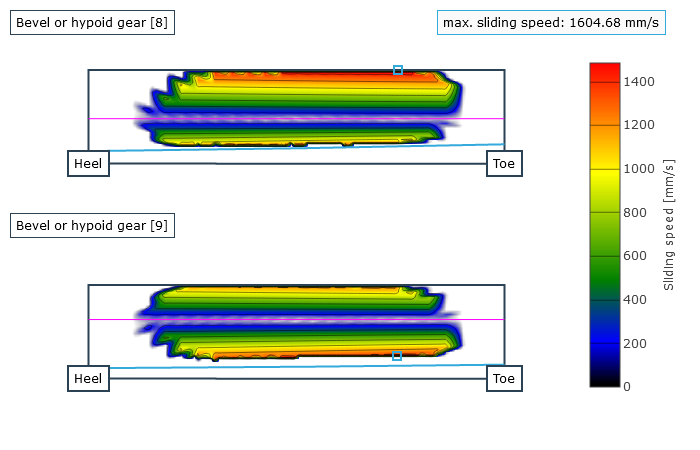
Gleitgeschwindigkeit im Kontaktbereich
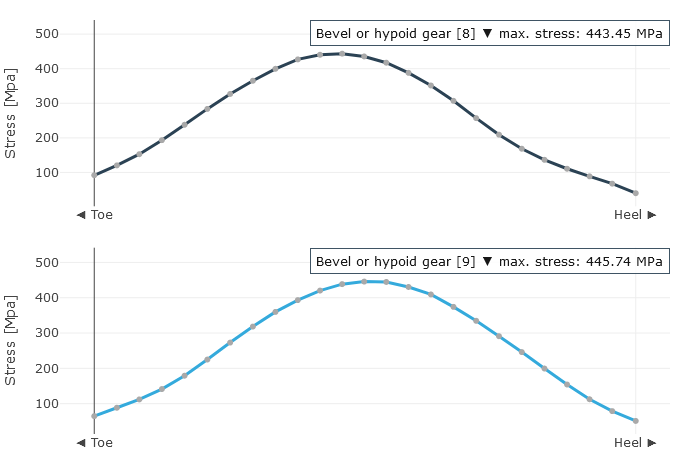
Zahnfußspannung über der Zahnbreite.
Berechnung des Betriebsflankenspiels
Das Betriebsflankenspiel bezeichnet das Rückflankenspiel (Verdrehflankenspiel) unter Last, das heißt, dass bei der Berechnung des Betriebsflankenspiels zusätzlich zu den lastbedingten Relativlageänderungen die Verformung der Zähne und des Radkörpers beachtet werden. Als Basis für das Betriebsflankenspiel wird die FE-Einflusszahlenmethode verwendet, die die Berechnung der Verformungen ermöglicht. Für die Betriebsflankenspielberechnung stehen zwei Methoden zur Verfügung: die lineare und die iterative Berechnungsmethode. Empfohlen wird die iterative Berechnungsmethode, die zwar Rechenzeit intensiver ist, aber genauere Ergebnisse liefert.
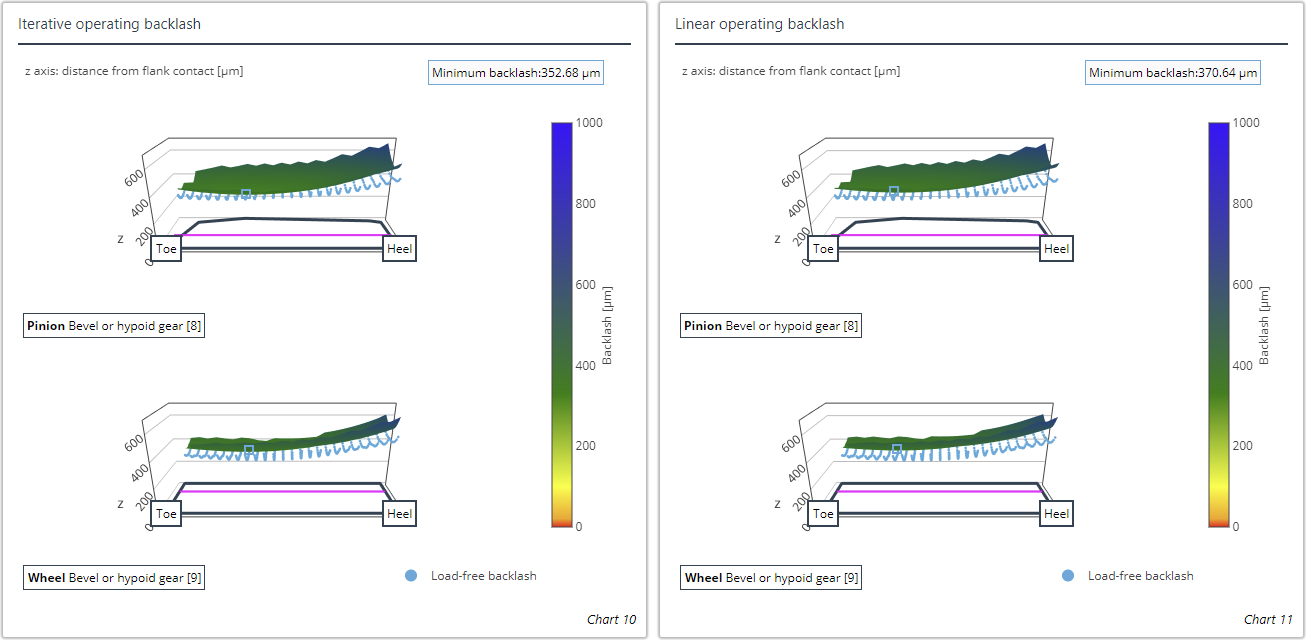
Zum schnellen Vergleich kann das lastfreie Rückflankenspiel (blau) im Diagramm eingeblendet werden. Der Ort mit dem minimalen Betriebsflankenspiel wird markiert.
Örtliche Tragfähigkeitsberechnung
Basierend auf den örtlich berechneten Beanspruchungen (Hertzsche Pressung, Zahnfußspannung), den lokalen Gleitgeschwindigkeiten sowie Angaben zu den Öl- und Werkstoffdaten, Rauigkeiten, Temperaturen und Schmierbedingungen können verschiedene Tragfähigkeitsnachweise geführt werden. Eine Überarbeitung der Örtlichen Tragfähigkeitsberechnungen erfolgte im Vorhaben FVA 223 XII (Forschungsvorhaben „BECAL - Schädigungsfortschritt Zahnflanke“, IMM der TU Dresden, Prof. Dr. Berthold Schlecht).
Hinweis
Berechnung mit individuellen Angaben zu Tribologie und Werkstoff
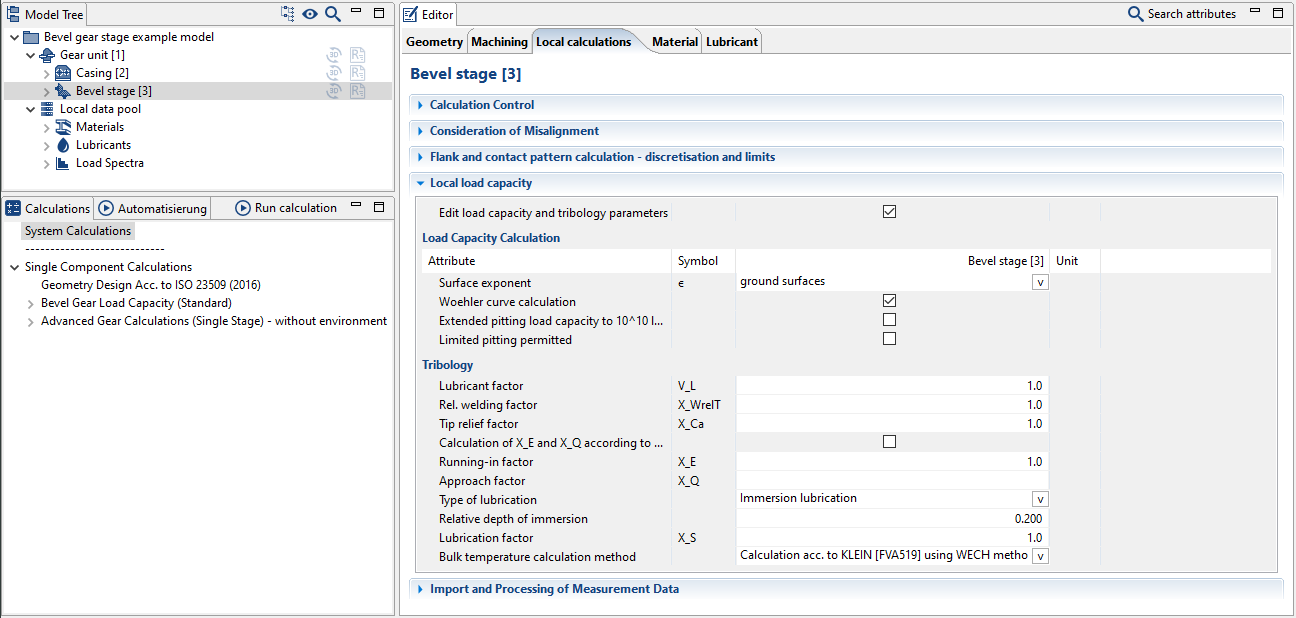
Die Vorgabe der Rauigkeit
Die Flankenrauheit beeinflusst die Reibungszahl sowie die Flankentragfähigkeiten. Die gemittelte Rautiefe im Zahnfuß wird für die Berechnung der Zahnfußtragfähigkeit nach ISO 10300-3 verwendet.
Die Vorgabe einer Wöhlerlinie oder optionale Angaben zur internen Wöhlerlinienberechnung
Bei der internen Wöhlerlinienberechnung wird diese anhand des Werkstoffes nach ISO 10300-2 bestimmt und es sind folgende weitere Angaben möglich. Die erweiterte Grübchentragfähigkeit bis 1010 Lastwechsel kann aktiviert werden. Der Faktor ZNT sinkt dabei im Dauerfestigkeitsgebiet auf einen Wert von ZNT = 0,85 ab. Mit dem Erlauben eines begrenzten Grübchenschadens kann eine gewisse Grübchenbildung toleriert werden (nach ISO 10300-2:2014). Die Vorgabe des Oberflächen-Exponenten ε erfolgt zur Berechnung der Graufleckentragfähigkeit nach FVA 516 und beinhaltet die Aussage über die Hartfeinbearbeitung der Flanke.
Die Vorgabe der Faktoren XW , XQ , XE , XS und XCA bzw. die Aktivierung der internen Berechnung
Der Einlauffaktor XE sowie der Treibrichtungsfaktor XQ beeinflussen die Fresstragfähigkeit und können entsprechend FVA 519 I intern berechnet werden.
Die Vorgabe der Methode zur Berechnung der Massentemperatur
Je nach Berechnungsmethode der Massentemperatur können Massentemperatur oder Reibungszahl vorgegeben werden. Dazu alternativ stehen folgende drei Berechnungsansätze zur Verfügung:
Die Massentemperatur nach KLEIN (FVA 519 I) wird anhand der Verlustleistung nach WECH bestimmt.
Der Ansatz von HOMBAUER (FVA 516 I) verfolgt die iterative Bestimmung der Verlustleistung, auf deren Grundlage die Massentemperaturberechnung erfolgt.
Bei der Annäherung nach KLEIN (FVA 519 I) wird die Massentemperatur in Abhängigkeit des Ritzeldrehmoments ermittelt.
Die Bestimmung der örtlichen Sicherheitswerte wird analog zu den standardisierten Berechnungsverfahren durchgeführt, dementsprechend werden die gleichen Festigkeitskennwerte verwendet. Die Grundlagen für diese örtliche Betrachtungsweise bilden experimentell gestützte Untersuchungen im FVA-Forschungsvorhaben 411 zur Tragfähigkeitsberechnung von Hypoidgetrieben.
Als Ergebnis werden Sicherheitswerte gegen Grübchen nach FVA 411 und Grauflecken nach FVA 516 (Forschungsvorhaben „Hypoidgraufleckigkeit“, FZG der TU München, Prof. Dr. Karsten Stahl) auf der Zahnflanke sowie die Sicherheit gegen Zahnfußbruch nach ISO 10300 berechnet sowie infolge überhöhter Kontakttemperatur die Sicherheit gegen Fressen nach FVA 519 (Forschungsvorhaben „Hypoidfressen“, FZG der TU München, Prof. Dr. Karsten Stahl). Die örtlichen Berechnungsergebnisse zu Graufleckensicherheit, Grübchensicherheit, Fresssicherheit und Zahnfußbruchsicherheit sowie die wesentlichen Zwischenergebnisse (örtliche Blitztemperaturen, örtliche Reibungszahlen und die relative Schmierfilmdicke) stehen als graphische Ausgaben zur Verfügung.
Zu empfehlen ist die Berechnung der örtlichen Tragfähigkeit im Gesamtsystem. Die Gesamtsystemberechnung betrachtet die Steifigkeit aller Komponenten im Getriebe und berechnet daraus die auftretenden Deformationen. Aus der Wellenbiegelinie werden die relativen Verlagerungen der Kegelradstufe berechnet und automatisch berücksichtigt. So können Kegelradstufen sehr einfach und unter Berücksichtigung aller maßgeblichen Einflüsse berechnet und bewertet werden.
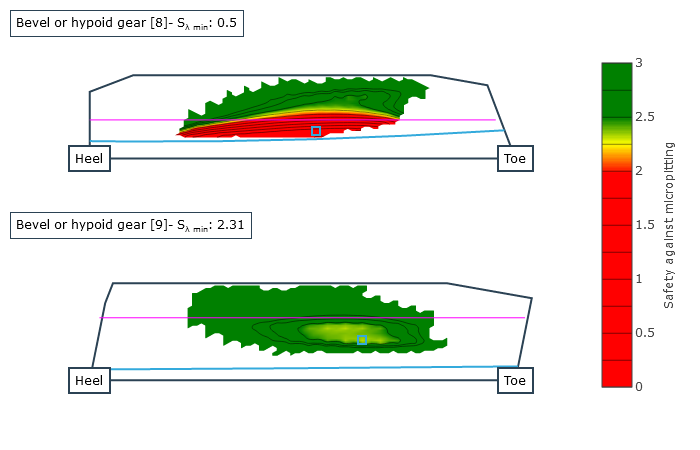 Örtliche Graufleckensicherheit | 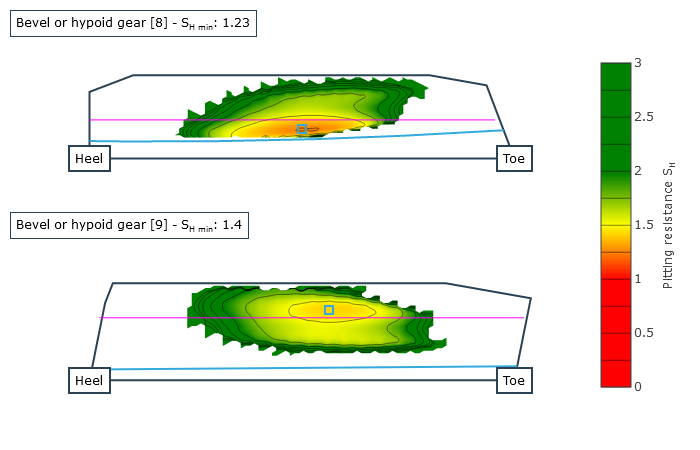 Örtliche Grübchensicherheit | 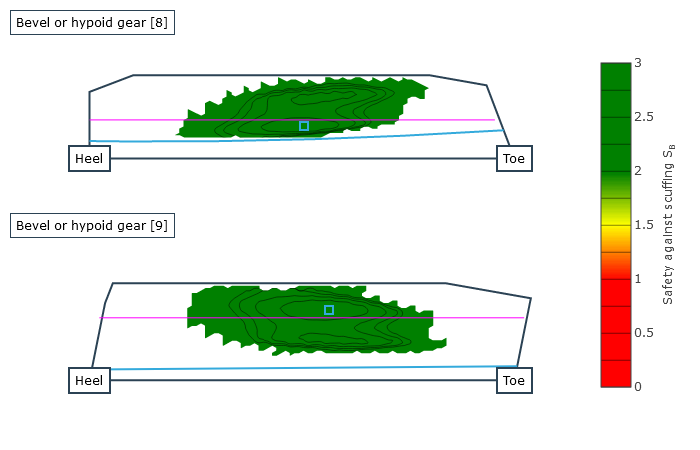 Örtliche Fressicherheit |
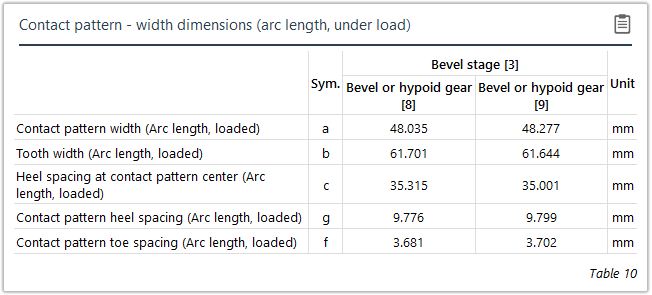
Tragbildvermessung
Das Leerlauftragbild ist in der Montage die maßgebliche Größe, mit der die Kegelradstufe eingestellt und die Kegelräder zueinander ausgerichtet werden. Wird die Solleinbaulage nicht eingehalten, kann das zur Verminderung der Tragfähigkeit, zu erhöhter Geräuschentwicklung oder auch Eingriffsstörungen führen. Um das Tragbild mit der Berechnung vergleichen zu können, wurden im Projekt FVA 223 XV (Forschungsvorhaben „Tragbildvermessung“, IMM der TU Dresden, Prof. Dr. Berthold Schlecht) Richtlinien entwickelt, wie Leerlauftragbilder und Lasttragbilder charakterisiert und gemessen werden können. Gleichzeitig wurde die Kegelradberechnung dahingehend erweitert, dass die relative Lage dieser Tragbilder zur Zahnberandung ausgegeben wird.
In den durchgeführten Versuchen wurde im Forschungsvorhaben gezeigt, dass die Leerlauf- und Lasttragbilder in der FVA-Workbench sehr gut mit den tatsächlichen Tragbildern zusammenpassen.
Hinweis
Berechnung des lastfreien Tragbilds
Es wird empfohlen, die Erweiterte Verzahnungsberechnung „Lastfreie Zahnkontaktsimulation“ als Einzelkomponentenberechnung ohne Vorgabe von belastungsabhängigen Relativlagen durchzuführen.
Alternativ kann auch eine Gesamtsystemberechnung mit entsprechend niedrigem Antriebsmoment durchgeführt werden.
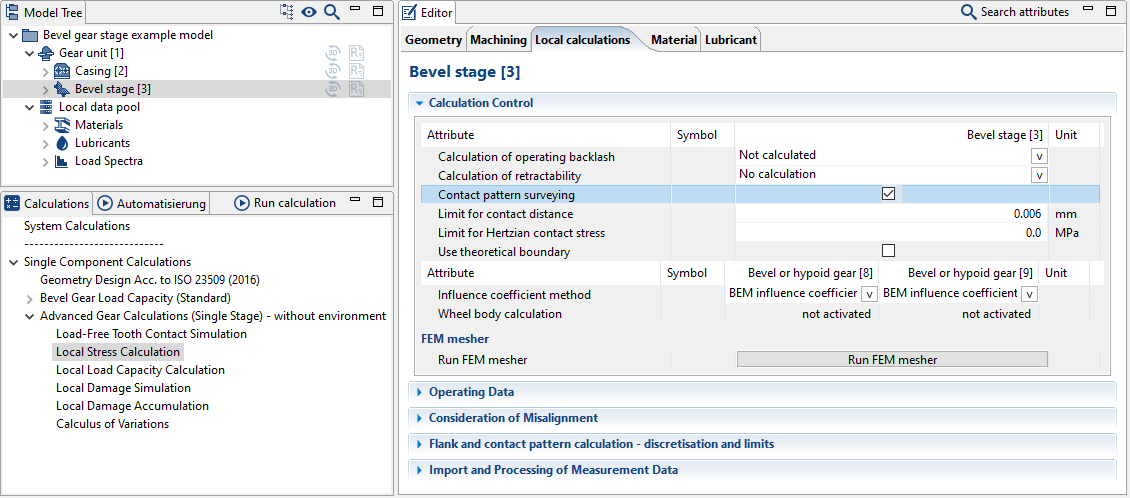
Die Tragbildberechnung kann im Editortab „Berechnungen“ aktiviert werden. Hier kann auch die vorliegende Tuschierpasten- bzw. Tuschierlackdicke als „Grenzwert Klaffmaß“ angegeben werden.
Berechnung des Lasttragbilds
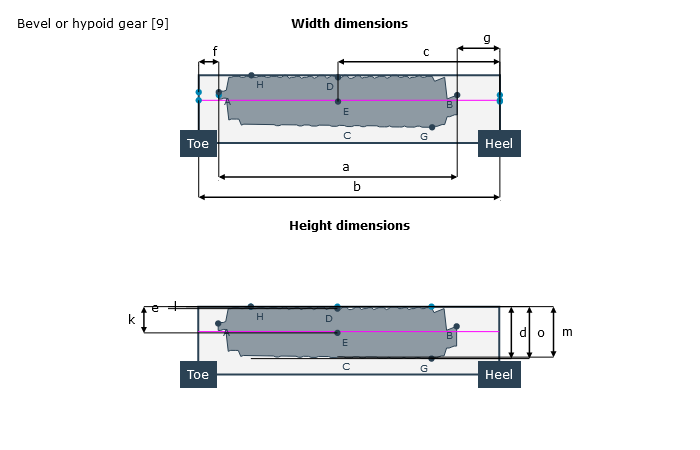
Es wird empfohlen, eine Gesamtsystemberechnung mit aktivierter Zusatzberechnung "Örtliche Beanspruchungsrechnung" mit dem vorliegenden Antriebsmoment durchzuführen. Die belastungsabhängigen Relativlageabweichungen werden aus dem Verzahnungsumfeld ermittelt und fließen in die Berechnung ein.
Die Tragbildberechnung kann im Editortab „Berechnungen“ aktiviert werden. Der gewünschte Tragbildbereich kann über „Grenzwert Hertzsche Pressung“ angegeben werden.
Die so berechneten Tragbilder bieten sich zur Kontrolle der Montage an. Darüber hinaus kann der Einfluss von Einbaumaßabweichungen und lastbedingten Relativlageänderungen auf das Tragbild erfasst werden.
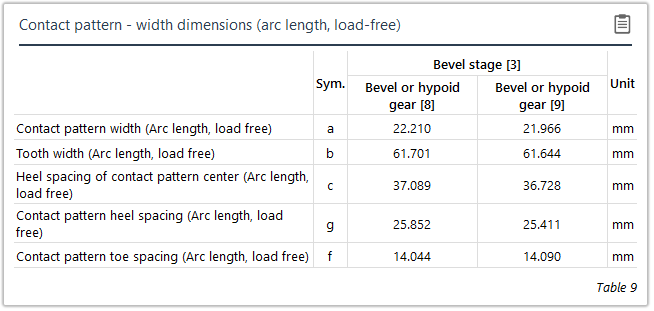
Zur Vermessung des Ist-Tragbildes auf der realen Zahnflanke können sowohl direkte Abstände (Sehnenmaß) als auch entlang der Flankenoberfläche gemessene Abstände (Abwicklungsmaß) verwendet werden.
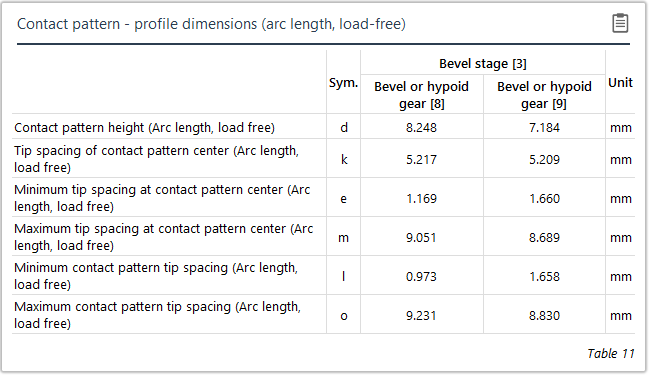
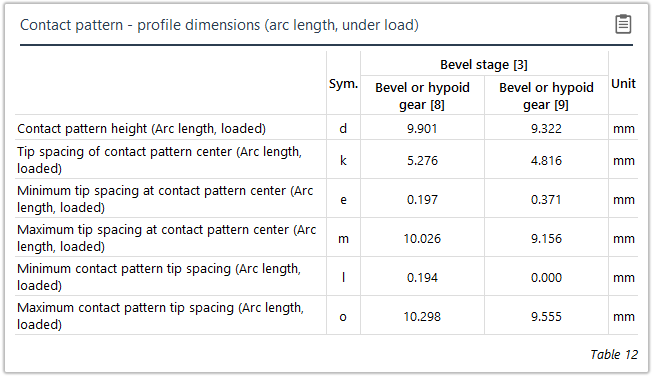
Lastfreies Tragbild | Lasttragbild |
|---|---|
 |  |
 |  |
 |  |
Variationsrechnung
Eine spezifische Eigenschaft von Kegelradverzahnungen ist die Verlagerungsempfindlichkeit, d.h. die Veränderung der Tragbildlage und -größe bei Relativlageänderungen. Die automatische Variation von Drehmoment und Drehzahl, verbunden mit belastungsabhängigen Relativlageabweichungen, gibt einen schnellen Überblick über die sich ändernden lokalen Beanspruchungen und Sicherheitsfaktoren.
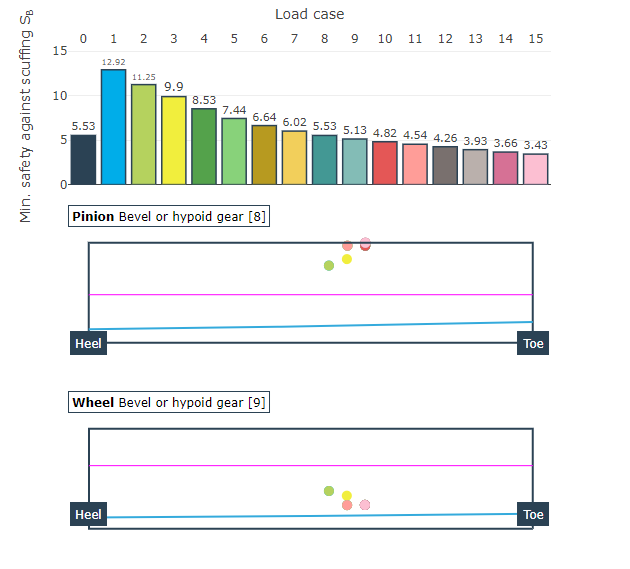
Darstellung der minimalen Sicherheit gegen Fressen für jeden Lastfall. Dabei wird der Zahlenwert und der Ort der minimalen Sicherheit auf der Flanke ausgegeben.
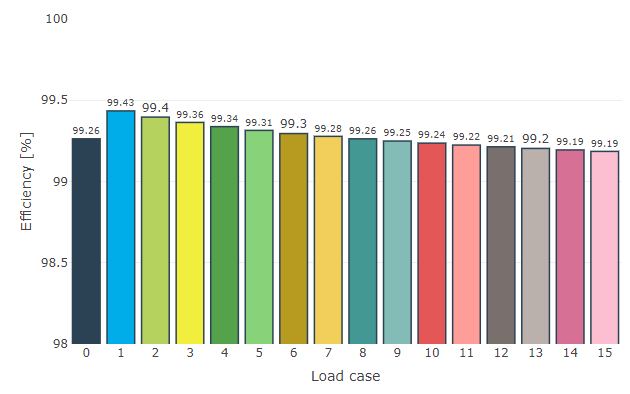
Darstellung des Wirkungsgrades für jeden Lastfall.
Örtliche Schadensakkumulation im Lastkollektiv
Mit der örtlichen Schadensakkumulationsberechnung können die realen, sich während der Betriebsdauer ändernden Belastungsverhältnisse, bei der Zahnkontaktsimulation und anschließenden örtlichen Tragfähigkeitsberechnung berücksichtigt werden. Auf diese Weise erhält der Nutzer einen ersten Anhaltspunkt über den Ort der größten Schädigung und damit des Bereiches, an dem Grübchenschäden bzw. Zahnfußschäden mit großer Wahrscheinlichkeit auftreten sowie eine Einschätzung der Höhe der Ermüdung.
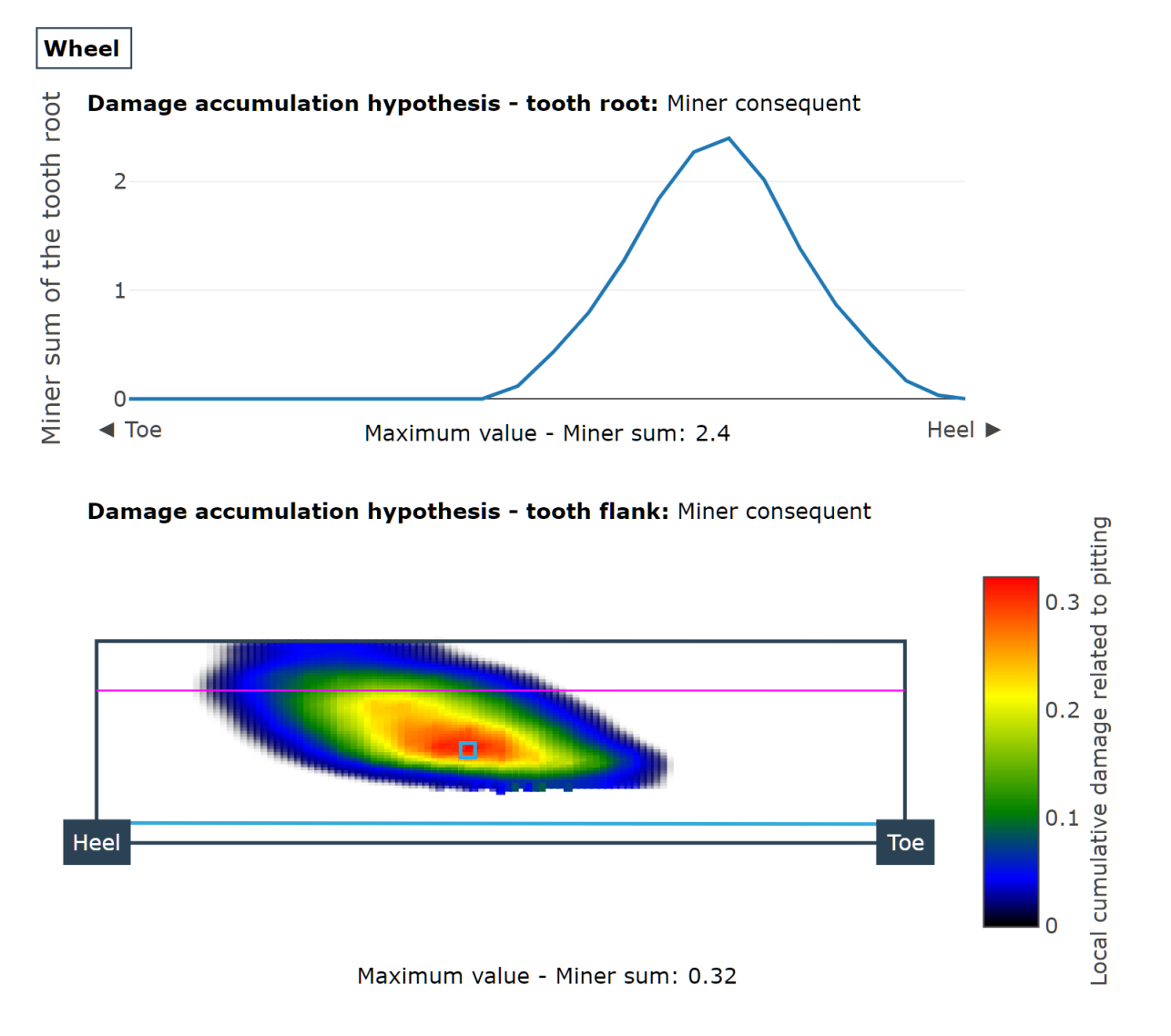
Schadensakkumulation für Zahnflanke und Zahnfuß
Örtliche Schädigungssimulation
In Erweiterung zur örtlichen Tragfähigkeitsrechnung kann, basierend auf dem FVA Forschungsvorhaben 223 XII, eine Schädigungssimulation auf der Zahnflanke durchgeführt werden. Die Simulation von Grauflecken- und Grübchenwachstum basiert auf der Ermittlung der Tragfähigkeit, der daraus berechneten Schädigungssumme und der Bestimmung der resultierenden Flankenformänderung. Da während der Simulation die Schädigung durch eine sich stetig verändernde Flankenform einbezogen wird, können sowohl die Wechselwirkungen zwischen den Schädigungsarten Grauflecken und Grübchen als auch der Einfluss der Schädigung auf die Flankentragfähigkeit abgebildet werden.
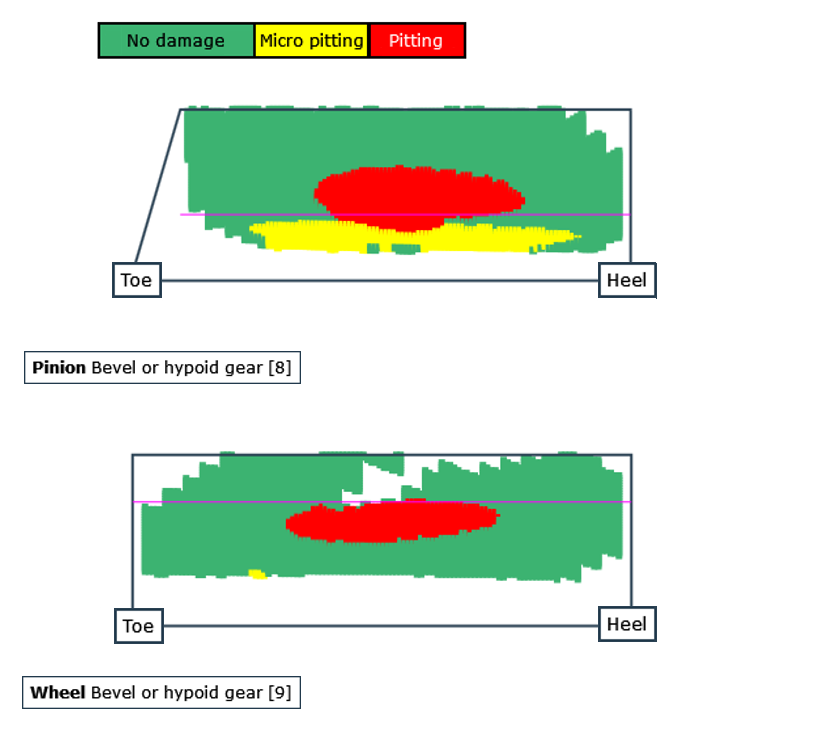
Schädigungsfortschritt auf der Flanke