Verlustleistung

Power losses and efficiency calculation in the FVA-Workbench

Gleichung 1.

P_{V} = (P_{V Z P} + P_{V Z 0}) + (P_{V L P} + P_{V L 0}) + P_{V P B} + P_{V D} + P_{V S T} + P_{V X}

Formelzeichen	Beschreibung	Einheit
P_V	Gesamtverlustleistung	W
P_VZP	Lastabhängige Verzahnungsverluste	W
P_VZ0	Lastunabhängige Verzahnungsverluste	W
P_VLP	Lastabhängige Wälzlagerverluste	W
P_VL0	Lastunabhängige Wälzlagerverluste	W
P_VPB	Gleitlagerverluste	W
P_VD	Dichtungsverluste	W
P_VST	Stegverluste oder Planetenträgerverluste	W
P_VX	Sonstige Verluste	W

Bei den Verlustleistungen, die durch die Zahnreibung und Lagerreibung verursacht werden, lässt sich eine Unterteilung in lastunabhängige (Index 0) sowie lastabhängige (Index P) Verlustleistungen vornehmen.

Dichtungen, Lager und Zahnräder haben auch ohne Belastung, bedingt durch Rollreibung und Gleitreibung, einen negativen Effekt auf den Gesamtwirkungsgrad.

In der folgenden Tabelle sind die unterschiedlichen Berechnungsansätze für die verschiedenen Komponenten aufgelistet mit der Angabe der entsprechenden Methoden/Quellen.

Verlustart	Komponente	Methode/Quelle
P_VZP	Stirnräder	H_v nach OHLENDORF, TALBOOM, WIMMER µ_mZ nach SCHLENK, DOLESCHEL
P_VZP	Kegel- und Hypoidräder	H_V und µ_mZ nach WECH
P_VZP	Schneckenstufen	DIN 3996, FVA 729 I
P_VZ0	Stirnräder, Kegel- und Hypoidräder	Tauchschmierung: Quetsch- und Planschverluste nach MAUZ, WALTER Einspritzschmierung: Quetschverluste nach MAUZ, BUTSCH Impulsverluste nach ARIURA, BUTSCH Ventilationsverluste nach MAURER
P_VLP,P_VL0	Wälzlager	SKF, SCHAEFFLER, TIMKEN, ISO14179-2
P_VPB	Gleitlager	COMBROS R&A
P_VD	Dichtungen	ISO 14179-1, ISO 14179-2, LINKE
P_VST	Planetenträger	KETTLER

Tabelle: Verlustleistungsberechnung, Methoden, Quellen

Die Verluste werden in der Gesamtsystemberechnung berücksichtigt. Dazu werden die Verlustmomente, an den Stellen ihres Auftretens im Leistungsfluss, vom übertragenen Drehmoment abgezogen. Die Drehzahl bleibt davon unberührt, d.h. es gibt keine bremsende verlangsamende Wirkung der Verluste auf das Gesamtsystem.

Der Wirkungsgrad des Getriebes berechnet sich aus dem Verhältnis der nutzbaren Leistung zur aufgebrachten Leistung.

Gleichung 2.

η = \frac{P_{A n} - P_{V}}{P_{A n}} \cdot 100

Formelzeichen	Beschreibung	Einheit
η	Wirkungsgrad	%
P_An	Antriebsleistung	W
P_V	Gesamtverlustleistung	W

Verzahnungsverluste

Die Verlustleistung der Verzahnungen berechnen sich aus den lastabhängigen und den lastunabhängigen Verlustanteilen. Bei der Berechnung werden die Verzahnungen in Stirnräder, Kegel- und Hypoidräder, sowie Schneckenräder unterschieden.

Lastabhängige Verzahnungsverluste für Stirnräder

Die lastabhängigen Verzahnungsverluste werden anhand der Grundgleichung, basierend auf der Coulombschen Reibung, bestimmt.

Gleichung 3.

P_{V Z P} = H_{V} \cdot μ_{m Z} \cdot P_{A n}

Formelzeichen	Beschreibung	Einheit
P_VZP	Lastabhängige Verzahnungsverluste	W
H_V	Zahnverlustfaktor	-
µ_mZ	Mittlere Verzahnungsreibungszahl	-
P_An	Antriebsleistung	W

Für den Zahnverlustfaktor und die mittlere Verzahnungsreibungszahl gibt es unterschiedliche Berechnungsmethoden, die im Folgenden näher beschrieben werden.

Zahnverlustfaktor nach OHLENDORF

Der Zahnverlustfaktor nach OHLENDORF wird sehr häufig verwendet, um die geometrische Auslegung einer Verzahnung hinsichtlich ihres Wirkungsgrades zu bewerten. Die hier gezeigte Methode entspricht der allgemeingültigen Erweiterung nach Wimmer.

Gleichung 4.

H_{V} = \frac{π \cdot (u + 1)}{z_{1} \cdot u \cdot cos β_{b}} \cdot (a_{0} + a_{1} | ϵ_{1} | + a_{2} | ϵ_{2} | + a_{3} | ϵ_{1} | ϵ_{1} + a_{4} | ϵ_{2} | ϵ_{2})

Formelzeichen	Beschreibung	Einheit
H_V	Zahnverlustfaktor	-
u	Zähnezahlverhältnis (z₂/z₁)	-
z_1/2	Zähnezahl von Ritzel/Rad	-
β_b	Grundkreisschrägungswinkel	deg
ε_1/2	Kopfüberdeckung von Ritzel/Rad	-
a_0…4	Koeffizienten für den Zahnverlustfaktor	-

mit den Koeffizienten für den Zahnverlustfaktor aus

Profilüberdeckung	Lage des Wälzpunktes C	a ₀	a ₁	a ₂	a ₃	a ₄
0 ≤ ε_α ≤ 1	vor dem Eingriffsgebiet	0	0	0	1/ε_α	1/ε_α
	im Eingriffsgebiet	0	0	0	1/ε_α	1/ε_α
	hinter dem Eingriffsgebiet	0	0	0	1/ε_α	1/ε_α
1 < ε_α ≤ 2	vor dem Eingriffsgebiet	0	1	1	0	0
	im 1. Doppeleingriffsgebiet	0	1	-1	0	1
	im Eingriffsgebiet	1	-1	-1	1	1
	im 2. Doppeleingriffsgebiet	0	-1	1	1	0
	hinter dem Eingriffsgebiet	0	1	1	0	0
2 < ε_α ≤3	vor dem Eingriffsgebiet	0	1	1	0	0
	im 1. Dreifacheingriffsgebiet	0	1	-1	0	2/3
	im 1. Doppeleingriffsgebiet	4/3	-1/3	-1	1/3	2/3
	im 2. Dreifacheingriffsgebiet	1	-1/3	-1/3	1/3	1/3
	im 2. Doppeleingriffsgebiet	4/3	-1	-1/3	2/3	1/3
	im 3. Dreifacheingriffsgebiet	0	-1	1	2/3	0
	hinter dem Eingriffsgebiet	0	1	1	0	0

Zahnverlustfaktor nach TALBOOM

Bei der Methode nach TALBOOM handelt es sich um eine Werksnorm von ZF.

Gleichung 5.

H_{V} = \frac{π \cdot (\frac{1}{z_{1}} + \frac{1}{z_{2}})}{cos β_{b}} \cdot 0.9 \cdot ϵ_{1}^{2} + 1.1 \cdot ϵ_{2}^{2} - (0.9 \cdot ϵ_{1} + 1.1 \cdot ϵ_{2}) \cdot (ϵ_{α} - 1) + \frac{2}{3} \cdot {(ϵ_{α} - 1)}^{2}

Die Formel gilt, wenn das Zahnrad 1 antreibt, ansonsten werden die Kopfüberdeckungen in der Formel auf das jeweilige andere Zahnrad gewechselt.

Formelzeichen	Beschreibung	Einheit
H_V	Zahnverlustfaktor	-
z_1/2	Zähnezahl von Ritzel/Rad	-
β_b	Grundkreisschrägungswinkel	deg
ε_1/2	Kopfüberdeckung von Ritzel/Rad	-
ε_α	Profilüberdeckung	-

Zahnverlustfaktor lokal-geometrisch nach WIMMER

Bei dem lokal-geometrischen Zahnverlustfaktor nach WIMMER wird die reale Lastverteilung inklusive der Verzahnungskorrekturen berücksichtigt. Der Wirkungsgrad verbessert sich, wenn die Last im Zahnkontakt in Richtung des Wälzpunktes verschoben wird. Dadurch lassen sich mit dieser Methode wirkungsgradoptimierte Verzahnungen auslegen

Bei Ohlendorf wird der Zahnkontakt nur auf der Eingriffsstrecke betrachtet und mit Annahmen eine vereinfachte Formel abgeleitet. Die Grundgleichung ist:

Gleichung 6.

H_{V} = \frac{1}{p_{e t}} \cdot \int_{x = A}^{E} F_{N} (x) \cdot v_{g} (x) d x

Bei Wimmer wird auch die Eingriffsbreite berücksichtigt und der Zahnverlustfaktor über numerische Verfahren ohne Vereinfachungen berechnet. Ausgangslage dafür ist die Folgende Gleichung:

Gleichung 7.

H_{V} = \frac{1}{p_{e t}} \cdot \int_{y = 0}^{b} \int_{x = A}^{E} \frac{F_{N} (x, y)}{F_{b t}} \cdot \frac{v_{g} (x, y)}{v_{t b}} d x d y

Formelzeichen	Beschreibung	Einheit
H_V	Zahnverlustfaktor	-
p_et	Eingriffsteilung am Grundkreis	mm
x	Koordinaten auf der Eingriffslinie: Abstand vom Wälzpunkt	mm
A,E	Koordinaten auf der Eingriffslinie: Anfang und Ende der Eingriffsstrecke	mm
F_N	Zahnnormalkraft	N
v_g	Gleitgeschwindigkeit	m/s
y	Koordinate auf der Eingriffsbreite	mm
b	Zahnbreite des Kontaktes	mm
F_bt	Umfangskraft am Grundkreis	N
v_tb	Umfangsgeschwindigkeit am Grundkreis	m/s

Mittlere Verzahnungsreibungszahl nach SCHLENK

Die Methode nach SCHLENK ist die gängigste Methode zur Berechnung der mittleren Verzahnungsreibungszahl. Es müssen nur wenige Eingangsgrößen bekannt sein und angegeben werden.

Gleichung 8.

μ_{m Z} = 0.048 \cdot {(\frac{F_{b t} / b}{v_{Σ C} \cdot ρ_{r e d C}})}^{0.2} \cdot η_{O i l}^{- 0.05} \cdot R a^{0.25} \cdot X_{L}

Formelzeichen	Beschreibung	Einheit
µ_mZ	Mittlere Verzahnungsreibungszahl	-
F_bt	Umfangskraft am Grundkreis	N
v_ΣC	Summengeschwindigkeit im Wälzpunkt	m/s
ρ_redC	Ersatzkrümmungsradius im Wälzpunkt	mm
η_Oil	Dynamische Betriebsölviskosität	mPas
X_L	Schmierstofffaktor	-
Ra	Arithmetischer Mittenrauheitswert der Verzahnungspartner 0.5 · (Ra₁ + Ra₂)	µm
b	Zahnbreite	mm

Mittlere Verzahnungsreibungszahl nach DOLESCHEL

Die Methode nach DOLESCHEL ist exakter bei der Bestimmung der mittleren Verzahnungsreibungszahl, als das einfache Verfahren nach SCHLENK. Zur Berechnung werden aber spezielle Referenzmessungen am Prüfstand benötigt, die in der Praxis nicht häufig durchgeführt werden.

Gleichung 9.

μ_{m Z} = (1 - ξ) \cdot μ_{F} + ξ \cdot μ_{E H D}

mit

Gleichung 10.

ξ ∊ [0; 1]

und

Gleichung 11.

μ_{E H D} = μ_{E H D, r e f} \cdot {(\frac{p_{H}}{p_{H, r e f}})}^{α_{E H D}} \cdot {(\frac{v_{Σ}}{v_{Σ, r e f}})}^{β_{Σ, E H D}} \cdot {(\frac{η_{O i l}}{η_{O i l, r e f}})}^{γ_{E H D}}

Gleichung 12.

μ_{F} = μ_{F, r e f} \cdot {(\frac{p_{H}}{p_{H, r e f}})}^{α_{F}} \cdot {(\frac{v_{Σ}}{v_{Σ, r e f}})}^{β_{Σ, F}}

mit

Gleichung 13.

ξ = 1 - {(1 - (0.5 \cdot \frac{h_{0}}{R a}))}^{2}

wenn

Gleichung 14.

h_{0} \leq 2 \cdot R a

oder

Gleichung 15.

ξ = 1

wenn

Gleichung 16.

h_{0} > 2 \cdot R a

Formelzeichen	Beschreibung	Einheit
µ_mZ	Mittlere Verzahnungsreibungszahl	-
ξ	Anteil der EHD-Reibung bei Mischreibung	-
µ_F,ref	Festkörperreibungszahl (bei Referenzbedingung)	-
µ_EHD,ref	EHD-Reibungszahl (bei Referenzbedingung)	-
p_H,ref	Hertzsche Pressung (bei Referenzbedingung)	MPa
v_Σ,ref	Summengeschwindigkeit (bei Referenzbedingung)	m/s
η_Oil,ref	Dynamische Betriebsölviskosität (bei Referenzbedingung)	mPas
α_EHD/F	Exponent für Pressungseinfluss	-
β_Σ,EHD/F	Exponent für Summengeschwindigkeitseinfluss	-
γ_EHD	Exponent für Viskositätseinfluss	-
h₀	Minimale Schmierfilmdicke	µm
Ra	Arithmetischer Mittenrauheitswert der Verzahnungspartner 0.5 · (Ra₁ + Ra₂)	µm

Die 11 Referenzgrößen aus dem Prüfstandsversuch müssen beim Schmierstoff in der Datenbank angegeben werden.

Lastabhängige Verzahnungsverluste für Kegel-/Hypoidräder

Die lastabhängigen Verzahnungsverluste von Kegel- und Hypoidradverzahnungen werden analog zu den entsprechenden Verlusten am Stirnrad betrachtet. Die Berechnung erfolgt nach WECH. Bei diesem Verfahren werden die Kegel- und Hypoidräder durch Ersatzschraubräder nach Niemann/Winter angenähert.

Die Verzahnungsverlustleistung berechnet sich aus der mittleren Reibungszahl, dem Zahnverlustfaktor und der Antriebsleistung:

Gleichung 17.

P_{V Z P} = μ_{m Z} \cdot H_{V} \cdot P_{A n}

Formelzeichen	Beschreibung	Einheit
P_VZP	Lastabhängige Verzahnungsverluste	W
µ_mZ	Mittlere Verzahnungsreibungszahl	-
H_V	Zahnverlustfaktor	-
P_An	Antriebsleistung	W

In die mittlere Reibungszahl µ_mZ gehen dabei folgende Einflüsse ein:

Über den Last- und Geometriefaktor Q_H werden die Last, die mittlere Gesamtgleitgeschwindigkeit sowie die mittlere Summengeschwindigkeit am Ersatzschraubrad und der Ersatzkrümmungsradius im Wälzpunkt berücksichtigt.
Die Schmierstoffeigenschaften V_L, die Schmierungsart V_S, die Betriebsölviskosität V_Z und die Rauigkeit der Zahnflanken V_R werden als Faktoren erfasst.

Gleichung 18.

μ_{m Z} = 0.054 \cdot V_{R} \cdot V_{S} \cdot V_{Z} \cdot V_{L} \cdot Q_{H}

Formelzeichen	Beschreibung	Einheit
µ_mZ	Mittlere Verzahnungsreibungszahl	-
V_R	Rauheitsfaktor	-
V_S	Schmierungsfaktor	-
V_Z	Viskositätsfaktor	-
V_L	Schmierstofffaktor	-
Q_H	Last- und Geometriefaktor	-

Gleichung 19.

Q_{H} = \frac{{(F_{N} \cdot \frac{cos β_{b 2}}{b_{2}})}^{0.05}}{K_{g m}^{0.6} \cdot ρ_{n}^{0.2} \cdot v_{Σ m}^{0.35}}

Formelzeichen	Beschreibung	Einheit
Q_H	Last- und Geometriefaktor	-
F_N	Normalkraft der Ersatzverzahnung	N
β_b2	Schrägungswinkel am Grundkreis des Rades	deg
b₂	Zahnbreite Rad	m
K_gm	Gleitfaktor	-
ρ_n	Ersatzkrümmungsradius	m
v_Σm	Mittlere Summengeschwindigkeit	m/s

Alternativ zur Berechnung der mittleren Reibungszahl nach WECH kann eine z. B. aus Versuchen bekannte oder firmenintern bestimmte Reibungszahl als Eingabegröße vorgegeben werden.

Der Zahnverlustfaktor H_V wird nach WECH ebenfalls an der Ersatzschraubverzahnung berechnet und berücksichtigt die Lastaufteilung und den Geschwindigkeitsverlauf über der Eingriffsstrecke dieser Ersatzverzahnung. Die Berechnung erfolgt letztlich durch Integration des Geschwindigkeitsverlaufes über der Eingriffstrecke.

Für genauere Details der Berechnung sei auf die Dissertation von Wech verwiesen:

WECH, L.: Untersuchungen zum Wirkungsgrad von Kegelrad- und Hypoidgetrieben, TU München, Diss., 1987

Lastabhängige Verzahnungsverluste für Schneckenstufen

Die Berechnung der lastabhängigen Verzahnungsverluste für Schneckenräder erfolgt nach DIN 3996.

Bei treibender Schnecke:

Gleichung 20.

P_{V Z P} = P_{A n} \cdot (1 - η_{Z})

mit

Gleichung 21.

η_{Z} = \frac{tan (γ_{m})}{tan (γ_{m}) + arctan (μ_{m Z})}

Bei treibendem Schneckenrad:

Gleichung 22.

P_{V Z P} = P_{A n} \cdot (1 - η_{Z}^{*})

mit

Gleichung 23.

η_{Z}^{*=} \frac{tan (γ_{m}) - arctan (μ_{m Z})}{tan (γ_{m})}

Formelzeichen	Beschreibung	Einheit
P_VZP	Lastabhängige Verzahnungsverluste	W
P_An	Antriebsleistung	W
η_Z	Verzahnungswirkungsgrad	-
γ_m	Steigungswinkel am Mittenkreis der Schnecke	deg
µ_mZ	Mittlere Verzahnungsreibungszahl	-

Für die mittlere Verzahnungsreibungszahl gibt es unterschiedliche Berechnungsmethoden, die im Folgenden näher beschrieben werden.

Mittlere Verzahnungsreibungszahl nach DIN 3996:2019

Bei der Überarbeitung der DIN 3996 im Jahr 2019 ist die Berechnung der mittleren Verzahnungsreibungszahl entsprechend der Dissertation von Oehler (2018) übernommen worden. Die Arbeiten zu dieser Dissertation sind u.a. im Rahmen des Projektes FVA 729 I durchgeführt worden und im Abschlussbericht (2017) dokumentiert.

Die mittlere Verzahnungsreibungszahl berechnet sich wie folgt:

Gleichung 24.

μ_{m Z} = Ψ \cdot μ_{G r} + (1 - Ψ) \cdot μ_{F l}

Formelzeichen	Beschreibung	Einheit
µ_mZ	Mittlere Verzahnungsreibungszahl	-
µ_Gr	Grenzreibungszahl	-
µ_Fl	Flüssigkeitsreibungszahl	-
Ψ	Festkörpertraganteil	-

Die Grenzreibungszahl ist abhängig von der Grundölsorte, von der mittleren Flankenpressung, sowie vom Werkstoff der Schnecke und des Schneckenrades.

Der Festkörpertraganteil hängt von der mittleren minimalen Schmierspaltdicke, der Oberflächentopographie der Schnecken- und Radzahnflanken und von dessen Material ab.

Die Flüssigkeitsreibungszahl wird aus der mittleren Schubspannung im Schmierspalt, aus der mittleren Flankenpressung und aus dem Festkörpertraganteil berechnet.

Mittlere Verzahnungsreibungszahl nach DIN 3996:2012

Die Berechnungsmethode der mittleren Verzahnungsreibungszahl nach der nicht mehr gültigen DIN 3996:2012 kann weiterhin zu Vergleichszwecken angewendet werden.

Die dazugehörige Formel lautet:

Gleichung 25.

μ_{m Z} = μ_{0 T} \cdot Y_{S} \cdot Y_{G} \cdot Y_{W} \cdot Y_{R}

Formelzeichen	Beschreibung	Einheit
µ_mZ	Mittlere Verzahnungsreibungszahl	-
µ_0T	Grundreibungszahl	-
Y_S	Baugrößenfaktor	-
Y_G	Geometriefaktor	-
Y_W	Werkstofffaktor	-
Y_R	Rauheitsfaktor	-

Lastunabhängige Verzahnungsverluste für Stirnräder und Kegel-/Hypoidräder

Unter der Verzahnungsleerlaufverlustleistung werden Plansch-, Quetsch-, Ventilations- und Impulsverluste zusammengefasst. Diese Verluste sind drehzahlabhängig aber nicht lastabhängig. Gegenüber den lastabhängigen Verzahnungsverlusten fallen die lastunabhängigen Verzahnungsverluste meist deutlich geringer aus.

In Abhängigkeit von der Schmierungsart und der vorliegenden Umfangsgeschwindigkeit werden die lastunabhängigen Verzahnungsverluste nach verschiedenen Berechnungsvorschriften ermittelt.

Tauchschmierung

Bei der Tauchschmierung werden Quetsch- und Planschverluste berücksichtigt.

Gleichung 26.

P_{V Z 0, t a u c h} = P_{V Z 0, q u e t s c h} + P_{V Z 0, p l a n s c h}

Formelzeichen	Beschreibung	Einheit
P_VZ0,tauch	Lastunabhängige Verzahnungsverluste bei Tauchschmierung	W
P_VZ0,quetsch	Quetschverluste: Ausquetschen des sich zu viel im Zahnkontakt befindlichen Öls	W
P_VZ0,plansch	Planschverluste: Planschen der Zahnräder im Öl	W

Für alle Zahnradstufen kann individuell vorgegeben werden, ob die Quetsch- und Planschverluste nach MAUZ oder nach WALTER bestimmt werden sollen. Als Standardverfahren ist die Berechnung nach MAUZ vorgegeben. Wird der Gültigkeitsbereich der Berechnungsgleichungen von MAUZ bzw. WALTER verlassen, erfolgen detaillierte Warnungen. Nach Möglichkeit wird die Berechnung aber nicht abgebrochen.

Lastunabhängige Verzahnungsverluste bei Tauchschmierung nach MAUZ

Das gesamte hydraulische Verlustmoment, sprich die Summe der Quetsch- und Planschverlustmomente werden je nach Lastpfad auf die Ritzel- oder Radwelle bezogen.

Bezogen auf die Ritzelwelle:

Gleichung 27.

T_{V Z 0, t a u c h} = (T_{V Z 0, p l a n s c h, R i t z e l} + \frac{z_{1}}{z_{2}} \cdot T_{V Z 0, p l a n s c h, R a d}) \cdot K_{P 1 G} + T_{V Z 0, q u e t s c h}

Bezogen auf die Radwelle:

Gleichung 28.

T_{V Z 0, t a u c h} = (T_{V Z 0, p l a n s c h, R i t z e l} \cdot \frac{z_{2}}{z_{1}} + T_{V Z 0, p l a n s c h, R a d}) \cdot K_{P 1 G} + T_{V Z 0, q u e t s c h}

Formelzeichen	Beschreibung	Einheit
T_VZ0,tauch	Lastunabhängiges Verzahnungsverlustmoment bei Tauchschmierung	Nm
T_VZ0,quetsch	Quetschverlustmoment	Nm
T_{VZ0,plansch,Ritzel/Rad}	Planschverlustmoment von Ritzel/Rad	Nm
K_P1G	Korrekturfaktor für das gleichzeitig tauchende Gegenrad	-
z_1/2	Zähnezahl von Ritzel/Rad	-

Die Verlustleistung berechnet sich entsprechend der Bezugswelle mit der Formel:

Gleichung 29.

P_{V Z 0} = T_{V Z 0, t a u c h} \cdot 2 \cdot π \cdot n

Formelzeichen	Beschreibung	Einheit
P_VZ0,tauch	Lastunabhängige Verzahnungsverluste bei Tauchschmierung	W
T_VZ0,tauch	Lastunabhängiges Verzahnungsverlustmoment bei Tauchschmierung	Nm
n	Wellendrehzahl	1/s

Quetschverluste nach MAUZ

Bei den Quetschverlusten nach MAUZ werden unterschiedliche Betriebsfälle berücksichtigt.

Beide Wellen sind waagrecht angeordnet und das eintauchende Rad fördert das Öl:

direkt in den Zahneingriff, Betriebsfall W1
indirekt über die Gehäusewand in den Zahneingriff, Betriebsfall W2

Oder die Wellen sind senkrecht angeordnet, dann ist die Drehrichtung vernachlässigbar und das entspricht den Betriebsfällen S1 und S2.

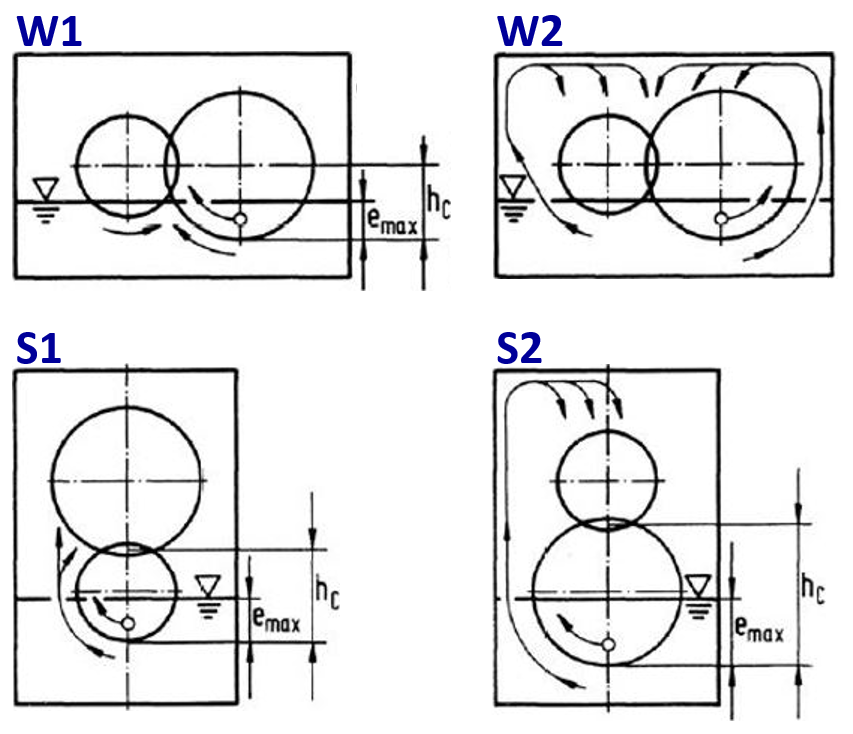Abbildung: Betriebsfälle

Das Quetschverlustmoment des Zahneingriffs berechnet sich aus:

Gleichung 30.

T_{V Z 0, q u e t s c h} = 0.0235 \cdot ρ_{O i l} \cdot b \cdot r_{w} \cdot v_{t}^{1.2} \cdot C_{S p}

mit

Betriebsfall W1: C_Sp = e/h_c
Betriebsfall W2: C_Sp = 0
Betriebsfall S1 und S2: C_Sp = (e/h_c)²

Formelzeichen	Beschreibung	Einheit
T_VZ0,quetsch	Quetschverlustmoment	Nm
ρ_Oil	Öldichte bei Betriebstemperatur	kg/m³
b	Minimale Zahnbreite von Ritzel und Rad	m
r_w	Radius am Wälzkreis des am tiefsten eintauchenden Zahnrads	m
v_t	Umfangsgeschwindigkeit am Wälzkreis	m/s
C_Sp	Spritzölfaktor	-
e	Eintauchtiefe des am tiefsten eintauchenden Zahnrads	mm
h_c	Höhe des Eingriffspunkts über dem am tiefsten eintauchenden Punkt der Stirnradstufe

Planschverluste nach MAUZ

Die Planschverlustmomente werden an Ritzel und Rad einzeln berechnet. Zur Berücksichtigung der gegenseitigen Beeinflussung der Zahnräder gibt es einen Korrekturfaktor.

Gleichung 31.

T_{V Z 0, p l a n s c h} = 1.86 \cdot 10^{- 3} \cdot {(\frac{ν_{O i l}}{ν_{0}})}^{- 1.255} \cdot (\frac{r_{a}}{r_{0}}) \cdot C_{W Z} \cdot C_{W A} \cdot C_{M} \cdot C_{V} \cdot ν_{O i l} \cdot ρ_{O i l} \cdot A_{B} \cdot v_{t}

Formelzeichen	Beschreibung	Einheit
T_VZ0,plansch	Planschverlustmoment	Nm
ν_Oil	Kinematische Viskosität bei Betriebstemperatur (ν₀ = 1)	m²/s
r_a	Radius am Kopfkreis (r₀ = 1)	m
C_WZ	Wandabstandsfaktor, Ölzulaufseite	-
C_WA	Wandabstandsfaktor, Ölablaufseite	-
C_M	Modulfaktor	-
C_V	Ölvolumenfaktor	-
ρ_Oil	Öldichte bei Betriebstemperatur	kg/m³
A_B	Im Betrieb eintauchende Radfläche	m²
v_t	Umfangsgeschwindigkeit am Wälzkreis	m/s

Gleichung 32.

C_{W Z} = (0.08 \cdot \frac{s_{r Z}}{r_{a}} - 0.1) \cdot (\frac{v_{t}}{v_{t 0}}) - 0.08 \cdot \frac{s_{r Z}}{r_{a}} + 1.1

für s_rZ ≤ 1.3 und v_t ≥ 10 m/s

Gleichung 33.

C_{W Z} = 1.0

für s_rZ > 1.3 oder v_t < 10 m/s

Formelzeichen	Beschreibung	Einheit
C_WZ	Wandabstandsfaktor, Ölzulaufseite	-
s_rZ	Abstand zwischen Kopfkreisdurchmesser und Gehäuse an der eintauchenden Seite des Zahnrades	m
r_a	Radius am Kopfkreis (r₀ = 1)	m
v_t	Umfangsgeschwindigkeit am Wälzkreis (v_t0 = 10)	m/s

Gleichung 34.

C_{W A} = (0.06 - 0.05 \cdot \frac{s_{r A}}{r_{a}}) \cdot (\frac{v_{t}}{v_{t 0}}) + 0.05 \cdot \frac{s_{r A}}{r_{a}} + 0.95

für s_rA ≤ 1.3 und v_t ≥ 10 m/s

Gleichung 35.

C_{W A} = 1.0

für s_rA > 1.3 oder v_t < 10 m/s

Formelzeichen	Beschreibung	Einheit
C_WA	Wandabstandsfaktor, Ölablaufseite	-
s_rA	Abstand zwischen Kopfkreisdurchmesser und Gehäuse an der austauchenden Seite des Zahnrades	m
r_a	Radius am Kopfkreis	m
v_t	Umfangsgeschwindigkeit am Wälzkreis (v_t0 = 10)	m/s

Gleichung 36.

C_{M} = {(\frac{m_{n}}{m_{n 0}})}^{\frac{1}{7}}

Formelzeichen	Beschreibung	Einheit
C_M	Modulfaktor	-
m_n	Normalmodul (m_n0 = 0.0045 · m_n)	m

Gleichung 37.

C_{V} = 1

für V_G/V_Oil ≥ 2.5

Gleichung 38.

C_{V} = 1 + \frac{1}{5} \cdot (\frac{V_{O i l} \cdot Q_{V 0}}{V_{G}} - 1) \cdot (\frac{v_{t}}{v_{t 0}} - 1)

mit Q_V ₀ = 0.74 · e^-0.438

für V_G/V_Oil < 2.5

Formelzeichen	Beschreibung	Einheit
C_V	Ölvolumenfaktor	-
V_G	Gehäusevolumen	m³
V_Oil	Ölvolumen im Gehäuse	m³
Q_V0	Faktor zur Berücksichtigung die Eintauchtiefe	-
e	Eintauchtiefe	m
v_t	Umfangsgeschwindigkeit am Wälzkreis (v_t0 = 10)	m/s

Gleichung 39.

A_{B} = r_{a}^{2} \cdot (α - sin α) + α \cdot r_{a} \cdot b

mit

Gleichung 40.

α = 2 \cdot arccos (1 - \frac{e_{B}}{r_{a}})

Gleichung 41.

e_{B} = e - (0.4 \cdot v_{t}) \cdot 10^{- 3}

für v_t ≤ 30 m/s

Gleichung 42.

e_{B} = e - 0.012 \cdot m_{n}

für v_t > 30 m/s

Formelzeichen	Beschreibung	Einheit
A_B	Im Betrieb eintauchende Radfläche	m²
r_a	Radius am Kopfkreis	m
α	Öffnungswinkel der eintauchenden Fläche	deg
b	Zahnbreite	m
e_B	Betriebseintauchtiefe	m
e	Eintauchtiefe	m
v_t	Umfangsgeschwindigkeit am Wälzkreis	m/s
m_n	Normalmodul	m

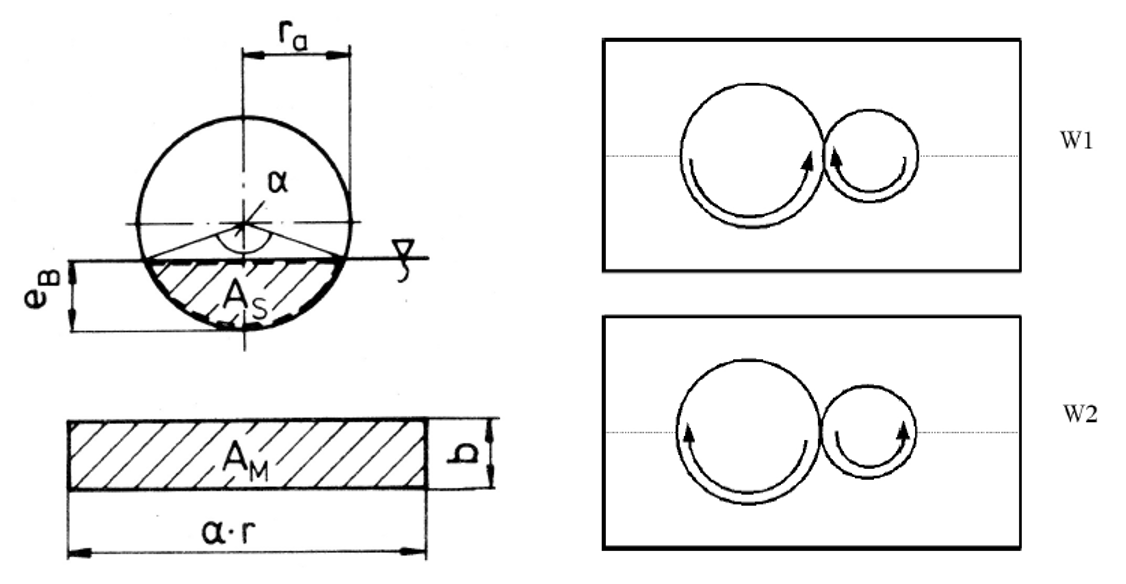Abbildung: Im Betrieb eintauchende Radfläche und Betriebsfall

Gleichung 43.

K_{P 1 G} = {(\frac{v_{t}}{v_{t 0}})}^{\frac{1}{3} \cdot \sqrt{\frac{log ν_{O i l} + 6}{log (99 \cdot ν_{0})}} \cdot \sqrt[3]{\frac{b}{3 \cdot b_{0}}}}

für Betriebsfall W1, Ölförderung direkt in den Zahneingriff

Gleichung 44.

K_{P 1 G} = 1.0

für Betriebsfall W2, Ölförderung indirekt über die Gehäusewand in den Zahneingriff

Formelzeichen	Beschreibung	Einheit
K_P1G	Korrekturfaktor für das gleichzeitig tauchende Gegenrad	-
v_t	Umfangsgeschwindigkeit am Wälzkreis (v_t0 = 10)	m/s
ν_Oil	Kinematische Viskosität bei Betriebstemperatur (ν₀ = 1)	m²/s
b	Zahnbreite (b₀ = 0.01)	m

Die Berechnungsmethode ist anhand von Versuchen abgeleitet worden. Die Grenzwerte der Versuche bilden auch den Gültigkeitsbereich der Methode ab. Wobei diese Grenzen konservativ sind und die Ergebnisse außerhalb des Gültigkeitsbereichs ebenso valide sein können.

Einflussgröße	Formelzeichen	Einheit	von	bis
Reynolds-Zahl	Re=(v_t·r_a)/ν	-	4125	531428
Relative Eintauchtiefe	e/r_a	-	0.04	1.0 (2.0)
Relativer radialer Wandabstand auf der Zu-/Ablaufseite	(s_rZ/rA)/r_a	-	0.03	3.15
Eintauchtiefe bezogen auf die Höhe des Wälzpunkts	e/h_c	-	0.02	1.0
Volumenverhältnis	V_G/V_Oil	-	2.0	12.0
Zähnezahlverhältnis	u	-	1.0	2.0
Kopfkreisradius	r_a	mm	66	124
Zahnbreite	b	mm	10	60
Normalmodul	m_n	mm	3	6
Umfangsgeschwindigkeit	v_t	m/s	10	60
Eintauchtiefe	e	mm	5	135
Kinematische Ölviskosität	ν	mm²/s	14	240
Dichte des Öls	ρ	kg/m³	855	881

Tabelle: Gültigkeitsbereich der Berechnungsgleichungen von Mauz

Lastunabhängige Verzahnungsverluste bei Tauchschmierung nach WALTER

Das gesamte hydraulische Verlustmoment, sprich die Summe der Quetsch- und Planschverlustmomente werden je nach Lastpfad auf die Ritzel- oder Radwelle bezogen.

Bezogen auf die Ritzelwelle:

Gleichung 45.

T_{V Z 0, t a u c h} = T_{V Z 0, p l a n s c h, R i t z e l} + T_{V Z 0, p l a n s c h, R a d} \cdot \frac{1}{u} + T_{V Z 0, q u e t s c h}

Bezogen auf die Radwelle:

Gleichung 46.

T_{V Z 0, t a u c h} = T_{V Z 0, p l a n s c h, R i t z e l} \cdot u + T_{V Z 0, p l a n s c h, R a d} + T_{V Z 0, q u e t s c h}

Formelzeichen	Beschreibung	Einheit
T_VZ0,tauch	Lastunabhängiges Verzahnungsverlustmoment bei Tauchschmierung	Nm
T_VZ0,quetsch	Quetschverlustmoment	Nm
T_{VZ0,plansch,Ritzel/Rad}	Planschverlustmoment von Ritzel/Rad	Nm
u	Zähnezahlverhältnis (z₂/z₁)	-

Die Verlustleistung berechnet sich entsprechend der Bezugswelle mit der Formel:

Gleichung 47.

P_{V Z 0} = T_{V Z 0, t a u c h} \cdot 2 \cdot π \cdot n

Formelzeichen	Beschreibung	Einheit
P_VZ0,tauch	Lastunabhängige Verzahnungsverluste bei Tauchschmierung	W
T_VZ0,tauch	Lastunabhängiges Verzahnungsverlustmoment bei Tauchschmierung	Nm
n	Wellendrehzahl	1/s

Quetschverluste nach WALTER

Das Quetschverlustmoment des Zahneingriffs berechnet sich aus:

Gleichung 48.

T_{V Z 0, q u e t s c h} = 3.88 \cdot 10^{- 10} \cdot C_{S p} \cdot ρ_{O i l} \cdot r_{w} \cdot b^{1.6} \cdot v_{t}^{2} \cdot ν_{O i l}^{- 0.15}

für direkte Spritzölzufuhr in den Zahneingriff

Gleichung 49.

C_{S p} = {(\frac{e}{h_{c}})}^{1.5}

für indirekte Spritzölzufuhr über die Gehäusewand in den Zahneingriff

Gleichung 50.

C_{S p} = {(\frac{e}{h_{c}})}^{1.5} \cdot (\frac{2 \cdot h_{c}}{l_{h}})

Formelzeichen	Beschreibung	Einheit
T_VZ0,quetsch	Quetschverlustmoment	Nm
C_Sp	Spritzölfaktor	-
ρ_Oil	Öldichte bei Betriebstemperatur	kg/m³
r_w	Radius am Wälzkreis des am tiefsten eintauchenden Zahnrads	m
b	Minimale Zahnbreite von Ritzel und Rad	m
v_t	Umfangsgeschwindigkeit am Wälzkreis	m/s
ν_Oil	Kinematische Viskosität bei Betriebstemperatur (ν₀ = 1)	m²/s
e	Eintauchtiefe des am tiefsten eintauchenden Zahnrads	m
h_c	Höhe des Eingriffspunkts über dem am tiefsten eintauchenden Punkt der Stirnradstufe	m
l_h	Hydraulische Länge	m

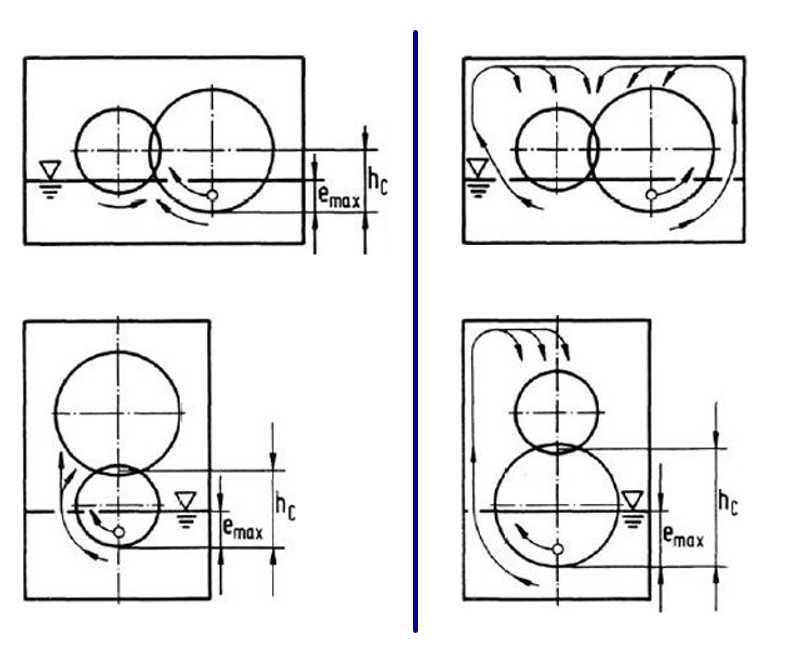Abbildung: Spritzölzufuhr direkt in den Eingriff (links), indirekt über die Gehäusewand (rechts)

Planschverluste nach WALTER

Die Planschverlustmomente werden an Ritzel und Rad einzeln berechnet.

Gleichung 51.

T_{V Z 0, p l a n s c h} = C_{W} \cdot C_{V} \cdot C_{P L} \cdot ρ_{O i l} \cdot v_{t}^{2} \cdot r_{a}^{2} \cdot b

Formelzeichen	Beschreibung	Einheit
T_VZ0,plansch	Planschverlustmoment	Nm
C_W	Wandabstandsfaktor	-
C_V	Ölvolumenfaktor	-
C_PL	Planschmomentfaktor	-
ρ_Oil	Öldichte bei Betriebstemperatur	kg/m³
v_t	Umfangsgeschwindigkeit am Wälzkreis	m/s
r_a	Radius am Kopfkreis	m
b	Zahnbreite	m

Gleichung 52.

C_{W} = 1

für s_rZ/(2 · r_a) ≥ 1

Gleichung 53.

C_{W} = 1 - 0.02 \cdot {(1 - \frac{s_{r Z}}{2 \cdot r_{a}})}^{1.8} \cdot {(\frac{v_{t}^{2}}{g \cdot r_{a}})}^{0.45}

für s_rZ/(2 · r_a) < 1

Formelzeichen	Beschreibung	Einheit
C_W	Wandabstandsfaktor	-
s_rZ	Abstand zwischen Kopfkreisdurchmesser und Gehäuse an der eintauchenden Seite des Zahnrades	m
r_a	Radius am Kopfkreis	m
v_t	Umfangsgeschwindigkeit am Wälzkreis	m/s
g	Gravitationskonstante	m³/(kg · s²)

Gleichung 54.

C_{V} = 1

für V_Z/V_Oil ≤ 0.1

Gleichung 55.

C_{V} = 1 - {(\frac{V_{Z}}{V_{O i l}} - 0.1)}^{0.4}

für V_Z/V_Oil > 0.1

Formelzeichen	Beschreibung	Einheit
C_V	Ölvolumenfaktor	-
V_Z	Volumen des vom Zahnrads verdrängten Öls	m³
V_Oil	Ölvolumen im Gehäuse	m³

Gleichung 56.

C_{P L} = 0.027 \cdot {(\frac{e}{r_{a}})}^{1.5} \cdot {(\frac{b}{r_{a}})}^{- 0.4} \cdot {(\frac{v_{t} \cdot r_{a}}{ν_{O i l}})}^{0.2} \cdot {(\frac{v_{t}^{2}}{g \cdot r_{a}})}^{- 0.5}

Formelzeichen	Beschreibung	Einheit
C_PL	Planschmomentfaktor	-
e	Eintauchtiefe	m
r_a	Radius am Kopfkreis	m
b	Zahnbreite	m
v_t	Umfangsgeschwindigkeit am Wälzkreis	m/s
ν_Oil	Kinematische Viskosität bei Betriebstemperatur	m²/s
g	Gravitationskonstante	m³/(kg · s²)

Wenn C_V = 1 und C_W = 1 sind, dann ergibt sich die vereinfachte Gleichung zu:

Gleichung 57.

T_{V Z 0, p l a n s c h} = 0.027 \cdot g^{0.5} \cdot ρ_{O i l} \cdot e^{1.5} \cdot b^{0.6} \cdot r_{a}^{1.6} \cdot v_{t}^{1.2} \cdot ν_{O i l}^{- 0.2}

Formelzeichen	Beschreibung	Einheit
T_VZ0,plansch	Planschverlustmoment	Nm
g	Gravitationskonstante	m³/(kg · s²)
ρ_Oil	Öldichte bei Betriebstemperatur	kg/m³
e	Eintauchtiefe	m
b	Zahnbreite	m
r_a	Radius am Kopfkreis	m
v_t	Umfangsgeschwindigkeit am Wälzkreis	m/s
ν_Oil	Kinematische Viskosität bei Betriebstemperatur	m²/s

Einflussgröße	Formelzeichen	Einheit	von	bis
Reynolds-Zahl	Re=(v_t·r_a)/ν	-	7980	471429
Froude-Zahl	Fr=v_t²/(g · r_a)	-	93	4645
Relative Eintauchtiefe	e/r_a	-	0.12	1.71
Relative Breite	b/r_a	-	0.09	0.63
Relative Zahnhöhe	h/m_n	-	2.25	-
Relativer radialer Wandabstand auf der Zulaufseite	s_rZ/(2r_a)	-	0.16	1.56
Relatives Ölvolumen	V_Z/V_Oil	-	0.01	0.20
Hydraulische Länge	l_H=(4A_G)/U	mm	629	1332
Kopfkreisradius	r_a	mm	79	110
Zahnbreite	b	mm	5	10
Normalmodul	m_n	mm	3	6
Umfangsgeschwindigkeit	v_t	m/s	10	60
Kinematische Ölviskosität	ν	mm²/s	14	99
Dichte des Öls	ρ	kg/m³	850	-

Tabelle: Gültigkeitsbereich der Berechnungsgleichungen von Walter

Einspritzschmierung

Bei Einspritzschmierung wird das Berechnungsverfahren automatisch über die vorliegende Umfangsgeschwindigkeit v_t bestimmt. So werden für v_t > 60 m/s die Quetsch- und die Impulsverluste nach BUTSCH berechnet, für v_t < 60 m/s die Quetschverluste nach MAUZ und die Impulsverluste nach ARIURA. Wird der Gültigkeitsbereich der Berechnungsgleichungen für Quetschverluste von BUTSCH verlassen, erfolgen detaillierte Warnungen. Nach Möglichkeit wird die Berechnung aber nicht abgebrochen.

Gleichung 58.

P_{V Z 0, e i n s p r i t z} = P_{V Z 0, i m p u l s} + P_{V Z 0, q u e t s c h} + P_{V Z 0, v e n t i l a t i o n}

Formelzeichen	Beschreibung	Einheit
P_{VZ0,einspritz}	Lastunabhängige Verzahnungsverluste bei Einspritzschmierung	W
P_VZ0,impuls	Impulsverluste: Strömungsumlenkung eines auf die Zahnflanken auftreffenden Ölstrahles	W
P_VZ0,quetsch	Quetschverluste: Ausquetschen des sich zu viel im Zahnkontakt befindlichen Öls	W
P_{VZ0,ventilation}	Ventilationsverluste: Verwirbelung des einspritzenden Öls	W

Planschverluste treten bei Einspritzschmierung nicht auf bzw. sind vernachlässigbar und werden folglich nicht berechnet.

Die Berechnung der Ventilationsverluste erfolgt nach MAURER, falls die Berechnung nicht deaktiviert wird.

Quetschverluste nach MAUZ für v_t < 60 m/s

Bei den Quetschverlusten werden zwei Einspritzvarianten unterschieden, die Einspritzung in den beginnenden Eingriff und in den auslaufenden Eingriff.

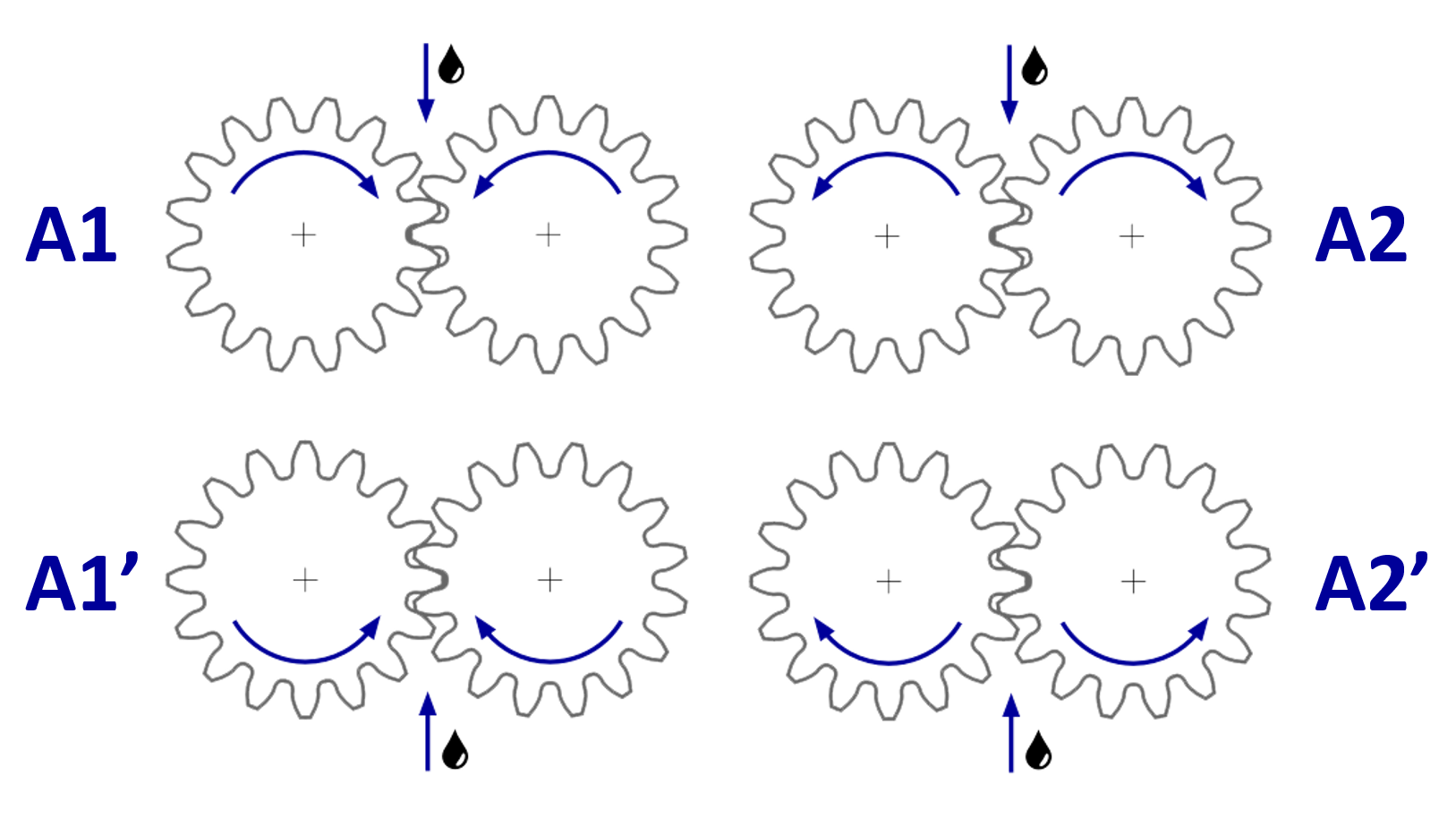Abbildung: Einspritzvarianten

Einspritzen in den beginnenden Eingriff (A1 und A1’)

Gleichung 59.

T_{V Q} = C_{1} \cdot 4.12 \cdot ρ_{O i l} \cdot Q_{e}^{0.75} \cdot r_{w} \cdot v_{t}^{1.25} \cdot b^{0.25} \cdot m_{n}^{0.25} \cdot {(\frac{ν_{O i l}}{ν_{0}})}^{0.25} \cdot {(\frac{h_{Z}}{h_{Z 0}})}^{0.5}

mit C1 = 1 für Einspritzvariante A1

mit C1 = 0.9 für Einspritzvariante A1‘

Einspritzen in den auslaufenden Eingriff (A2 und A2’)

Gleichung 60.

T_{V Q} = C_{2} \cdot ρ_{O i l} \cdot Q_{e} \cdot r_{w} \cdot (v_{t} + v_{s})

mit C2 = 1 für Einspritzvariante A2

mit C2 = 0.85 für Einspritzvariante A2‘

Formelzeichen	Beschreibung	Einheit
T_VQ	Quetschverlustmoment	Nm
C_1/2	Konstanten abhängig von der Einspritzvariante	-
ρ_Oil	Öldichte bei Betriebstemperatur	kg/m³
Q_e	Eingespritzter Ölvolumenstrom	m³/s
r_w	Radius am Wälzkreis	m
v_t	Umfangsgeschwindigkeit am Wälzkreis	m/s
v_s	Einspritzgeschwindigkeit	m/s
b	Zahnbreite	m
m_n	Normalmodul	m
ν_Oil	Kinematische Viskosität bei Betriebstemperatur (ν₀ = 1)	m²/s
h_Z	Gemeinsame Zahnhöhe (h_Z0 = 2.3 ·m_n)	m

Quetschverluste nach BUTSCH für v_t > 60 m/s

Es werden wie bei MAUZ zwei Einspritzvarianten unterschieden, die Einspritzung in den beginnenden Eingriff und in den auslaufenden Eingriff. Für beide Fälle werden die folgenden bezogenen Größen eingeführt:

Gleichung 61.

v_{t}^{*=} \frac{v_{t}}{100 [m / s]}

Gleichung 62.

Q_{e}^{*=} Q_{e} \cdot \frac{6 \cdot 10^{2}}{1 [m^{3} / s]}

Gleichung 63.

b^{*=} \frac{b}{0.1 [m]}

Gleichung 64.

r^{*=} \frac{2 \cdot u}{u + 1}

Einspritzen in den beginnenden Eingriff (A1)

Gleichung 65.

T_{V Q} = C_{1} \cdot v_{t}^{*} + C_{2}

mit

Gleichung 66.

C_{1} = 18 \cdot {(\frac{Q_{e}^{*}}{b^{*}})}^{\frac{0.8}{b^{*}}} \cdot {(b^{*})}^{1.8} \cdot {(r^{*})}^{1.1} - 12.75 \cdot Q_{e}^{*} \cdot r^{*}

Gleichung 67.

C_{2} = 8 \cdot {(\frac{Q_{e}^{*}}{b^{*}})}^{0.5} \cdot {(b^{*})}^{- 0.3} \cdot {(r^{*})}^{1.1} + 2.35 \cdot Q_{e}^{*} \cdot r^{*}

Einspritzen in den auslaufenden Zahneingriff (A2)

Gleichung 68.

T_{V Q} = C_{3} + C_{4} \cdot (v_{t}^{*} - 0.6) + C_{5} \cdot ({(v_{t}^{*})}^{2} - {0.6}^{2})

mit

Gleichung 69.

C_{3} = 0.5 - {(r^{*})}^{- 2}

Gleichung 70.

C_{4} = 17.2 \cdot {(r^{*})}^{1.5} - 12.75 \cdot (\frac{Q_{e}^{*}}{b^{*}}) \cdot r^{*}

Gleichung 71.

C_{5} = - 6.3 \cdot \frac{{(r^{*})}^{1.5}}{1 + (\frac{Q_{e}^{*}}{b^{*}})}

Formelzeichen	Beschreibung	Einheit
T_VQ	Quetschverlustmoment	Nm
C_3/4/5	Konstanten abhängig von der Einspritzvariante	-
v_t*	Bezogene dimensionslose Umfangsgeschwindigkeit am Wälzkreis	-
v_t	Umfangsgeschwindigkeit am Wälzkreis	m/s
Q_e*	Bezogener dimensionsloser eingespritzter Ölvolumenstrom	-
Q_e	Eingespritzter Ölvolumenstrom	m³/s
b*	Bezogene dimensionslose Zahnbreite	-
b	Zahnbreite	m
r*	Bezogener dimensionsloser Radius	-
u	Zähnezahlverhältnis (z₂/z₁)	-

Der Gültigkeitsbereich für beide Einspritzvarianten ist:

Ölviskosität ISO VG 22 bis 86
Zahnbreite 0.075 m ≤ b ≤ 0.125 m
Umfangsgeschwindigkeit 60 m/s ≤ v_t ≤ 200 m/s
Vollstrahldüsen

Impulsverluste nach AIURA für v_t < 60 m/s

Einspritzen in den beginnenden Eingriff (A1 und A1‘)

Gleichung 72.

T_{V I} = r_{w} \cdot ρ_{O i l} \cdot Q_{e} \cdot (v_{t} - v_{s}) \cdot C_{1}

Einspritzen in den auslaufenden Zahneingriff (A2 und A2‘)

Gleichung 73.

T_{V I} = r_{w} \cdot ρ_{O i l} \cdot Q_{e} \cdot (v_{t} + v_{s}) \cdot C_{1}

mit C1 = 1 für Einspritzvariante A1

mit C1 = 0.9 für Einspritzvariante A1‘

mit C1 = 1 für Einspritzvariante A2

mit C1 = 0.85 für Einspritzvariante A2‘

Formelzeichen	Beschreibung	Einheit
T_VI	Impulsverlustmoment	Nm
C₁	Konstante abhängig von der Einspritzvariante	-
r_w	Radius am Wälzkreis	m
ρ_Oil	Öldichte bei Betriebstemperatur	kg/m³
Q_e	Eingespritzter Ölvolumenstrom	m³/s
v_t	Umfangsgeschwindigkeit am Wälzkreis	m/s
v_s	Einspritzgeschwindigkeit	m/s

Sollte die Einspritzgeschwindigkeit die Zahnräder antreiben, würden sich daraus negative Verluste ergeben. In diesem Fall werden die Impulsverluste zu 0 gesetzt.

Impulsverluste nach BUTSCH für v_t > 60 m/s

Einspritzen in den beginnenden Eingriff (A1 und A1‘)

Gleichung 74.

T_{V I} = r_{w 2} \cdot ρ_{O i l} \cdot Q_{e} \cdot (v_{t} - v_{s})

Einspritzen in den auslaufenden Zahneingriff (A2 und A2‘)

Gleichung 75.

T_{V I} = r_{w 2} \cdot ρ_{O i l} \cdot Q_{e} \cdot (v_{t} + v_{s})

Formelzeichen	Beschreibung	Einheit
T_VI	Impulsverlustmoment	Nm
r_w2	Radius am Wälzkreis des Rades	m
ρ_Oil	Öldichte bei Betriebstemperatur	kg/m³
Q_e	Eingespritzter Ölvolumenstrom	m³/s
v_t	Umfangsgeschwindigkeit am Wälzkreis	m/s
v_s	Einspritzgeschwindigkeit	m/s

Sollte die Einspritzgeschwindigkeit die Zahnräder antreiben, würden sich daraus negative Verluste ergeben. In diesem Fall werden die Impulsverluste zu 0 gesetzt.

Ventilationsverluste nach MAURER

Die Anteile der Ventilationsverluste für das Ritzel und das Rad berechnen sich aus:

Gleichung 76.

T_{V V, R i t z e l} = 1.37 \cdot 10^{- 9} \cdot v_{t}^{1.90} \cdot d_{w 1}^{1.60} \cdot b_{1}^{0.52} \cdot m_{t}^{0.69}

Gleichung 77.

T_{V V, R a d} = 1.37 \cdot 10^{- 9} \cdot v_{t}^{1.90} \cdot d_{w 2}^{1.60} \cdot b_{2}^{0.52} \cdot m_{t}^{0.69}

Der durch das Gegenrad verursachte Momentenanteil berechnet sich aus:

Gleichung 78.

T_{V V, E i n g r i f f} = 1.17 \cdot 10^{- 6} \cdot v_{t}^{1.95} \cdot u^{0.73} \cdot b^{1.37}

Das Ventilationsverlustmoment des Radpaares wird auf die Radwelle bezogen. Zur Ermittlung der Verluste des Radpaares ist deshalb das Ventilationsverlustmoment des Ritzels mit dem Zähnezahlverhältnis zu multiplizieren. Das Ventilationsverlustmoment des Radpaars berechnet sich dann folgendermaßen:

Gleichung 79.

T_{V V, R a d p a a r} = (T_{V V, R a d} + u \cdot T_{V V, R i t z e l} + T_{V V, E i n g r i f f}) \cdot F_{W a n d} \cdot F_{O i l}

mit

Gleichung 80.

F_{W a n d} = 0.763 \cdot s_{u}^{0.26} \cdot s_{v w}^{- 0.0043 \cdot (2.11 \cdot s_{u} - 9.53)}

Gleichung 81.

F_{O i l} = 0.934 \cdot Q_{e}^{0.163}

Formelzeichen	Beschreibung	Einheit
T_{VV,Ritzel/Rad}	Ventilationsverlustmoment von Ritzel/Rad	Nm
v_t	Umfangsgeschwindigkeit am Wälzkreis	m/s
d_w1/2	Wälzkreisdurchmesser von Ritzel/Rad	mm
b_1/2	Zahnbreite von Ritzel/Rad	mm
T_VV,Eingriff	Ventilationsverlustmoment durch das Gegenrad	Nm
u	Zähnezahlverhältnis (z₂/z₁)	-
b	Minimale Zahnbreite von Ritzel und Rad	mm
T_VV,Radpaar	Ventilationsverlustmoment des Radpaares	Nm
F_Wand	Faktor für Wandeffekte	-
F_Oil	Faktor für Öleffekte	-
s_u	Minimaler stirnseitiger Abstand zur Gehäusewand	mm
s_vw	Minimaler radialer Abstand zur Gehäusewand	mm
Q_e	Eingespritzter Ölvolumenstrom	l/min

Lastunabhängige Verzahnungsverluste für Schneckenstufen

Nach FVA 729 I wird ein Modell zur Berechnung der Planschverlustleistung von Stirnradstufen auf Schneckenstufen angewendet:

Gleichung 82.

P_{V Z 0} = (\frac{1}{2} \cdot ρ_{O i l} \cdot {(\frac{π \cdot n}{30})}^{2} \cdot A \cdot {(\frac{d_{m}}{2})}^{3} \cdot C_{m}) \cdot ω

mit

Gleichung 83.

C_{m} = {(\frac{2 \cdot e}{d_{m}})}^{0.45} \cdot {(\frac{V_{0}}{d_{m}})}^{0.1} \cdot F r^{- 0.6} \cdot R e^{- 0.21}

Gleichung 84.

F r = \frac{ω^{2} \cdot d_{m}}{2 \cdot g}

Gleichung 85.

R e = \frac{ω^{2} \cdot d_{m}^{2}}{4 \cdot ν_{O i l}}

Formelzeichen	Beschreibung	Einheit
P_VZ0	Lastunabhängige Verzahnungsverluste	W
ρ_Oil	Öldichte bei Betriebstemperatur	kg/m³
n	Drehzahl	1/min
A	Vom Öl benetzte Oberfläche	mm²
d_m	Mittenkreis- /Wälzkreisdurchmesser	m
ω	Rotationsgeschwindigkeit	1/s
C_m	Planschfaktor	-
e	Eintauchtiefe	m
V₀	Ölvolumen	m³
Fr	Froude-Zahl	-
g	Gravitationskonstante	m³/(kg · s²)
Re	Reynolds-Zahl	-
ν_Oil	Kinematische Viskosität bei Betriebstemperatur	m²/s

Es werden nur die Planschverluste des Schneckenrades gerechnet. Die Schnecke wird nicht berücksichtigt, vergleichbar wie Wellen.

Wälzlagerverluste

Die Verlustleistung durch Wälzlager wird mithilfe der aktuellen Katalogmethoden der Hersteller SKF, SCHAEFFLER und TIMKEN bestimmt. Ist dies nicht möglich oder nicht gewollt, dann kann auch die Verlustleistungsberechnung nach ISO 14179-2 gewählt werden, die der SKF Katalogmethode von 1994 entspricht.

Abbildung: Aktuelle Lagerkataloge aus 2020 von SKF, SCHAEFFLER und TIMKEN

Im Weiteren werden die Berechnungsmethoden nur grob skizziert. Für genauere Details der Berechnung, sei auf die kostenlos verfügbaren Lagerkataloge der Hersteller verwiesen.

SKF 2020

Die Katalogmethode von SKF gilt sicherlich als der detaillierteste und genauste Berechnungsansatz, um die Verlustleistung zu ermitteln. Zur Bestimmung des gesamten Verlustmoments werden die einzelnen Anteile der Reibmomente addiert. Dadurch lässt sich auch erkennen, welcher Anteil am Verlustmoment den entscheidenden größten Anteil hat und wo sich eventuelle Verbesserungen erzielen lassen.

Gleichung 86.

M = M_{r r} + M_{s l} + M_{s e a l} + M_{d r a g}

Formelzeichen	Beschreibung	Einheit
M	Gesamtreibmoment	Nm
M_rr	Rollreibmoment	Nm
M_sl	Gleitreibungsmoment	Nm
M_seal	Reibmoment der Berührungsdichtungen	Nm
M_drag	Reibmoment bedingt durch Strömungs−, Plansch− oder Spritzverluste	Nm

Gleichung 87.

M_{r r} = ϕ_{i s h} \cdot ϕ_{r s} \cdot G_{r r} \cdot (ν_{O i l} \cdot n)^{0.6}

Formelzeichen	Beschreibung	Einheit
M_rr	Rollreibmoment	Nm
ϕ_ish	Schmierfilmdickenfaktor für Rollreibungsmoment	-
ϕ_rs	Kinematischer Schmierstoffverdrängungsfaktor für Rollreibungsmoment	-
G_rr	Rollreibungsgrundwert abhängig von der Lagergeometrie und der Eingangsbelastung	-
ν_Oil	Kinematische Betriebsölviskosität	mm²/s
n	Relative Drehzahl zwischen Lagerinnen- und Lageraußenring	1/min

Gleichung 88.

M_{s l} = G_{s l} \cdot μ_{s l}

Formelzeichen	Beschreibung	Einheit
M_sl	Gleitreibungsmoment	Nm
G_sl	Gleitreibungsgrundwert abhängig von der Lagergeometrie und der Eingangsbelastung	-
µ_sl	Gleitreibungszahl	-

Gleichung 89.

M_{s e a l} = K_{S 1} \cdot d_{S}^{β} + K_{S 2}

Formelzeichen	Beschreibung	Einheit
M_seal	Reibmoment der Berührungsdichtungen	Nm
K_S1	Dichtungsreibungsbeiwert 1 abhängig von Dichtungs- und Lagertyp sowie Lagergröße	-
d_S	Durchmesser der Gegenlauffläche der Dichtung	mm
β	Dichtungsreibungsexponent abhängig von Dichtungs- und Lagertyp	-
K_S2	Dichtungsreibungsbeiwert 2 abhängig von Dichtungs- und Lagertyp sowie Lagergröße	-

Kugellager

Gleichung 90.

M_{d r a g} = 0.4 \cdot V_{M} \cdot K_{b a l l} \cdot d_{m}^{5} \cdot n^{2} + 1.093 \cdot 10^{- 7} \cdot n^{2} \cdot d_{m}^{3} \cdot {(\frac{n \cdot d_{m}^{2} \cdot f_{t}}{ν_{O i l}})}^{- 1.379} \cdot R_{S}

Zylinderrollenlager

Gleichung 91.

M_{d r a g} = 4 \cdot V_{M} \cdot K_{r o l l} \cdot d_{m}^{4} \cdot n^{2} + 1.093 \cdot 10^{- 7} \cdot n^{2} \cdot d_{m}^{3} \cdot {(\frac{n \cdot d_{m}^{2} \cdot f_{t}}{ν_{O i l}})}^{- 1.379} \cdot R_{S}

Formelzeichen	Beschreibung	Einheit
M_drag	Reibmoment bedingt durch Strömungs−, Plansch− oder Spritzverluste bei einer Ölbadschmierung	Nm
V_M	Strömungsverlustfaktor	-
K_ball, K_roll	Wälzkörperbezogene Konstanten abhängig von Lagertyp und -größe, sowie Anzahl der Wälzkörper	-
d_m	Mittlerer Lagerdurchmesser 0.5·(d+D)	mm
n	Relative Drehzahl zwischen Lagerinnen- und Lageraußenring	1/min
f_t	Faktor zur Eintauchtiefe im Ölbad abhängig von Lagergröße und dem Ölstand	-
ν_Oil	Kinematische Betriebsölviskosität	mm²/s
R_S	Ölbadfaktor abhängig von Lagertyp/-größe und Ölstand	-

Ausführlichere Details zur Berechnung werden im SKF Lagerkatalog beschrieben.

Zudem gibt es ein SKF Online-Tool zur Lagerberechnung, indem auch die Verlustleistung enthalten ist.

SCHAEFFLER 2020

Die Katalogmethode von SCHAEFFLER basiert auf einfachen empirisch ermittelten Kennwerten zur Berechnung des Gesamtreibmoments abhängig von lastunabhängigen, sowie lastabhängigen Verlustanteilen, wobei axiale Belastungen separat berücksichtig werden.

Gleichung 92.

M_{R} = M_{0} + M_{1} + M_{2}

Formelzeichen	Beschreibung	Einheit
M_R	Gesamtreibmoment	Nm
M₀	Lastunabhängiges Lagerreibungsmoment	Nm
M₁	Lastabhängiges Lagerreibungsmoment	Nm
M₂	Lagerreibungsmoment für axial belastete Zylinderrollenlager	Nm

Drehzahlabhängiges Reibmoment

Gleichung 93.

M_{0} = 10^{- 7} \cdot f_{0} \cdot (ν_{O i l} \cdot n)^{\frac{2}{3}} \cdot d_{m}^{3}

für

Gleichung 94.

ν_{O i l} \cdot n \geq 2000 \frac{m m^{2}}{s \cdot min}

oder

Gleichung 95.

M_{0} = 160 \cdot 10^{- 7} \cdot f_{0} \cdot d_{m}^{3}

für

Gleichung 96.

ν_{O i l} \cdot n < 2000 \frac{m m^{2}}{s \cdot min}

Formelzeichen	Beschreibung	Einheit
M₀	Lastunabhängiges Lagerreibungsmoment	Nm
f₀	Lastunabhängiger Lagerreibungsfaktor	-
ν_Oil	Kinematische Betriebsölviskosität	mm²/s
n	Relative Drehzahl zwischen Lagerinnen- und Lageraußenring	1/min
d_m	Mittlerer Lagerdurchmesser 0.5·(d+D)	mm

Lastabhängiges Reibmoment

für Nadel- und Zylinderrollenlager

Gleichung 97.

M_{1} = f_{1} \cdot F \cdot d_{m}

für Kugel-, Kegel- und Pendelrollenlager

Gleichung 98.

M_{1} = f_{1} \cdot P_{1} \cdot d_{m}

Formelzeichen	Beschreibung	Einheit
M₁	Lastabhängiges Lagerreibungsmoment	Nm
f₁	Lastabhängiger Lagerreibungsfaktor	-
F	Radiallast für Radiallager und Axiallast für Axiallager	N
d_m	Mittlerer Lagerdurchmesser 0.5·(d+D)	mm
P₁	Maßgebliche Last für das Reibmoment	N

Gleichung 99.

M_{2} = f_{2} \cdot F_{a} \cdot d_{m}

Formelzeichen	Beschreibung	Einheit
M₂	Lagerreibungsmoment für axial belastete Zylinderrollenlager	Nm
f₂	Lagerreibungsfaktor abhängig von der Axiallast	-
F_a	Axiale dynamische Lagerbelastung	N
d_m	Mittlerer Lagerdurchmesser 0.5·(d+D)	mm

Ausführlichere Details zur Berechnung werden im SCHAEFFLER Lagerkatalog beschrieben.

Zudem gibt es ein SCHAEFFLER Online-Tool zur Lagerberechnung, indem auch die Verlustleistung enthalten ist.

TIMKEN 2020

Die Katalogmethode von TIMKEN basiert auf einfachen empirisch ermittelten Kennwerten zur Berechnung des Gesamtreibmoments abhängig von lastunabhängigen, sowie lastabhängigen Verlustanteilen. Das Formelwerk ähnelt in vielen Punkten der Berechnung nach SCHAEFFLER.

Gleichung 100.

M = f_{1} \cdot F_{β} \cdot d_{m} + 10^{- 7} \cdot f_{0} \cdot (ν_{O i l} \cdot n)^{\frac{2}{3}} \cdot d_{m}^{3}

für

Gleichung 101.

ν_{O i l} \cdot n \geq 2000 \frac{m m^{2}}{s \cdot min}

oder

Gleichung 102.

M = f_{1} \cdot F_{β} \cdot d_{m} + 160 \cdot 10^{- 7} \cdot f_{0} \cdot d_{m}^{3}

für

Gleichung 103.

ν_{O i l} \cdot n < 2000 \frac{m m^{2}}{s \cdot min}

mit

Radialkugellager

Gleichung 104.

F_{β} = max (0.9 \cdot F_{a} \cdot cot α - 0.1 \cdot F_{r}; F_{r})

Radial−Zylinderrollen− und Pendelrollenlager

Gleichung 105.

F_{β} = max (0.8 \cdot F_{a} \cdot cot α; F_{r})

Axial−Kugel−, Zylinder− und Pendelrollenlager

Gleichung 106.

F_{β} = F_{a}

Formelzeichen	Beschreibung	Einheit
M	Gesamtreibmoment	Nm
f₁	Lastabhängiger Lagerreibungsfaktor	-
F_β	Lagerbelastung für das lastabhängige Lagerreibmoment	N
F_a, F_r	Axiale bzw. radiale Lagerbelastung	N
α	Nennkontaktwinkel	deg
f₀	Lastunabhängiger Lagerreibungsfaktor	-
d_m	Mittlerer Lagerdurchmesser 0.5·(d+D)	mm
ν_Oil	Kinematische Betriebsölviskosität	mm²/s
n	Relative Drehzahl zwischen Lagerinnen- und Lageraußenring	1/min

für Kegelrollenlager

einreihig

Gleichung 107.

M = k_{1} \cdot G_{1} \cdot (n \cdot ν_{O i l})^{0.62} \cdot {(\frac{f_{3} \cdot F_{r}}{K})}^{0.3}

zweireihig

Gleichung 108.

M = k_{1} \cdot G_{1} \cdot (n \cdot ν_{O i l})^{0.62} \cdot {(\frac{0.06}{K})}^{0.3} \cdot (F_{r A}^{0.3} + F_{r B}^{0.3})

Formelzeichen	Beschreibung	Einheit
M	Gesamtreibmoment	Nm
k₁	Lagerdrehmoment Konstante	-
G₁	Geometriefaktor	-
ν_Oil	Kinematische Betriebsölviskosität	mm²/s
n	Relative Drehzahl zwischen Lagerinnen- und Lageraußenring	1/min
f₃	Kombinierter Lastfaktor	-
F_r	Radiallast	N
K	K-Faktor	-
F_rA, F_rB	Radiallast Reihe A bzw. B	N

Ausführlichere Details zur Berechnung werden im TIMKEN Lagerkatalog beschrieben.

ISO 14179-2

Die Berechnung der Lagerverluste nach ISO 14179-2 entspricht der SKF Lagerkatalogmethode von 1994.

Gleichung 109.

M = M_{0} + M_{1} + M_{2}

Formelzeichen	Beschreibung	Einheit
M	Gesamtreibmoment	Nm
M₀	Lastunabhängiges Lagerreibungsmoment	Nm
M₁	Lastabhängiges Lagerreibungsmoment	Nm
M₂	Lagerreibungsmoment für axial belastete Zylinderrollenlager	Nm

Drehzahlabhängiges Reibmoment

Gleichung 110.

M_{0} = 10^{- 10} \cdot f_{0} \cdot {(ν_{O i l} \cdot n)}^{\frac{2}{3}} \cdot d_{m}^{3}

für

Gleichung 111.

ν_{O i l} \cdot n \geq 2000 \frac{m m^{2}}{s \cdot min}

oder

Gleichung 112.

M_{0} = 1.6 \cdot 10^{- 8} \cdot f_{0} \cdot d_{m}^{3}

für

Gleichung 113.

ν_{O i l} \cdot n < 2000 \frac{m m^{2}}{s \cdot min}

Formelzeichen	Beschreibung	Einheit
M₀	Lastunabhängiges Lagerreibungsmoment	Nm
f₀	Lastunabhängiger Lagerreibungsfaktor abhängig vom Lagertyp und der Beölungsart	-
d_m	Mittlerer Lagerdurchmesser 0.5·(d+D)	mm
ν_Oil	Kinematische Betriebsölviskosität	mm²/s
n	Relative Drehzahl zwischen Lagerinnen- und Lageraußenring	1/min

Lastabhängiges Reibmoment

Gleichung 114.

M_{1} = f_{1} \cdot P_{1}^{a} \cdot d_{m}^{b} \cdot 10^{- 3}

Formelzeichen	Beschreibung	Einheit
M₁	Lastabhängiges Lagerreibungsmoment	Nm
f₁	Lastabhängiger Lagerreibungsfaktor	-
P₁	Äquivalente Lagerbelastung für das Reibmoment	N
a, b	Exponenten	-
d_m	Mittlerer Lagerdurchmesser 0.5·(d+D)	mm

Gleichung 115.

M_{2} = f_{2} \cdot F_{a} \cdot d_{m} \cdot 10^{- 3}

Formelzeichen	Beschreibung	Einheit
M₂	Lagerreibungsmoment für axial belastete Zylinderrollenlager	Nm
f₂	Lagerreibungsfaktor abhängig von der Axiallast	-
F_a	Axiale dynamische Lagerbelastung	N
d_m	Mittlerer Lagerdurchmesser 0.5·(d+D)	mm

Bei der Auswahl dieser Berechnungsmethode müssen die Faktoren f₀ und f₁ per Hand vorgegeben werden. Die dazugehörigen Tabellen aus der ISO 14179-2 sind in der Attributhilfe angegeben.

Gleitlagerverluste

Die Verlustleistung durch Gleitlager wird in den Modulen COMBROS R & A berechnet, welche seit längerem in der iterativen Lösung des Gesamtsystems der FVA-Workbench integriert sind. Die in COMBROS berechneten Reibmomente werden bei der Bestimmung des verlustbehafteten Gesamtsystems mitberücksichtigt.

Combros R&A

Die Berechnungsmodule COMBROS R (radial) und A (axial) sind am Institut für Tribologie und Energiewandlungsmaschinen (ITR) der TU Clausthal entwickelt worden. Die Entwicklung geschah im Rahmen der FVA Projekte FVA 577, FVA 668II und FVA 677.

Planetenträgerverluste

Die Verlustleistung durch Planetenträger bei einwangigen Stegen entsteht durch das Planschen des Stegs und der Planeten im Öl . Bei zweiwangigen Stegen haben die Planeten keinen zusätzlichen Einfluss auf die Planschverluste, da sie sich innerhalb des Planetenträgers befinden.

Die Verluste durch die Eigendrehung der Planeten werden gesondert berücksichtigt und dem Planeten selbst zugeschlagen.

Die Methodik zur Berechnung der Planetenträgerverluste stammt von KETTLER.

Einwangige Planetenträger nach KETTLER

Bei einwangigen offenen Planetenträgern werden die Planschverluste des Stegs und der im Steg mitrotierenden Planeten addiert.

Gleichung 116.

P_{V S T} = P_{V S T, s w 1} + P_{V S T, s r 1}

Formelzeichen	Beschreibung	Einheit
P_VST	Planschverlustleistung einwangiger Planetenradträger	W
P_VST,sw1	Planschverlustleistung der Stegwangen einwangiger Planetenradträger	W
P_VST,sr1	Planschverlustleistung der Planetenräder einwangiger Planetenradträger aufgrund der Stegdrehung	W

Gleichung 117.

P_{V S T, s w 1} = 4.6295 \cdot 10^{- 3} \cdot d_{S t 1}^{3.8} \cdot b_{S t 1} \cdot F_{e, S t 1}^{1.1945} \cdot n_{s 0}^{1.8559} \cdot ν_{O i l}^{0.22} \cdot ρ_{O i l}

Formelzeichen	Beschreibung	Einheit
P_VST,sw1	Planschverlustleistung der Stegwangen einwangiger Planetenradträger	W
d_St1	Gesamtdurchmesser des einwangigen Planetenradträgers	m
b_St1	Stegbreite des einwangigen Planetenradträgers	m
F_e,St1	Einflussfaktor Ölstand für Stegwangen von einwangigen Planetenradträgern	-
n_s0	Planetenradträgerdrehzahl	min^-1
ν_Oil	kinematische Betriebsölviskosität	mm²/s
ρ_Oil	Öldichte bei Betriebstemperatur	kg/m³

mit

Gleichung 118.

F_{e, S t 1} = 1

falls

Gleichung 119.

s_{O i l} > \frac{1}{2} \cdot d_{S t 1}

oder

Gleichung 120.

F_{e, S t 1} = \frac{1}{π} \cdot arccos (\frac{- 2 \cdot s_{O i l}}{d_{S t 1}})

falls

Gleichung 121.

s_{O i l} \leq \frac{1}{2} \cdot d_{S t 1}

und

Gleichung 122.

s_{O i l} \geq - \frac{1}{2} \cdot d_{S t 1}

oder

Gleichung 123.

F_{e, S t 1} = 0

falls

Gleichung 124.

s_{O i l} < - \frac{1}{2} \cdot d_{S t 1}

Formelzeichen	Beschreibung	Einheit
F_e,St1	Einflussfaktor Ölstand für Stegwangen von einwangigen Planetenradträgern	-
s_Oil	Ölstand bezogen auf die Getriebemitte	m
d_St1	Gesamtdurchmesser des einwangigen Planetenradträgers	m

Gleichung 125.

P_{V S T, s r 1} = 1.2096 \cdot 10^{- 2} \cdot F a k_{P l 1} \cdot | a |^{2.6} \cdot d_{a, P l} \cdot b_{P l} \cdot F_{e, a S t 1}^{0.9013} \cdot n_{s 0}^{2.3706} \cdot ρ_{O i l}

Formelzeichen	Beschreibung	Einheit
P_VST,sr1	Planschverlustleistung der Planetenräder einwangiger Planetenradträger aufgrund der Stegdrehung	W
Fak_Pl1	Einflussfaktor Planetenradanzahl für einwangige Planetenradträger	-
a	Achsabstand	m
d_a,Pl	Planetenradkopfdurchmesser	m
b_Pl	Planetenradbreite	m
F_e,aSt1	Einflussfaktor Ölstand für Planetenräder von einwangigen Planetenradträgern	-
n_s0	Planetenradträgerdrehzahl	min^-1
ρ_Oil	Öldichte bei Betriebstemperatur	kg/m³

mit

Gleichung 126.

F a k_{P l 1} = 1.1724

falls

Gleichung 127.

z_{P l} = 3

oder

Gleichung 128.

F a k_{P l 1} = 1.1829

falls

Gleichung 129.

z_{P l} > 3

und

Gleichung 130.

F_{e, a S t 1} = 1

falls

Gleichung 131.

s_{O i l} > a

oder

Gleichung 132.

F_{e, a S t 1} = \frac{1}{π} \cdot arccos (\frac{- s_{O i l}}{a})

falls

Gleichung 133.

s_{O i l} > - a

oder

Gleichung 134.

F_{e, a S t 1} = 0

falls

Gleichung 135.

s_{O i l} < - a

Formelzeichen	Beschreibung	Einheit
Fak_Pl1	Einflussfaktor Planetenradanzahl für einwangige Planetenradträger	-
z_Pl	Anzahl der Planeten	-
F_e,aSt1	Einflussfaktor Ölstand für Planetenräder von einwangigen Planetenradträgern	-
s_Oil	Ölstand bezogen auf die Getriebemitte	m
a	Achsabstand im Koordinatensystem	m

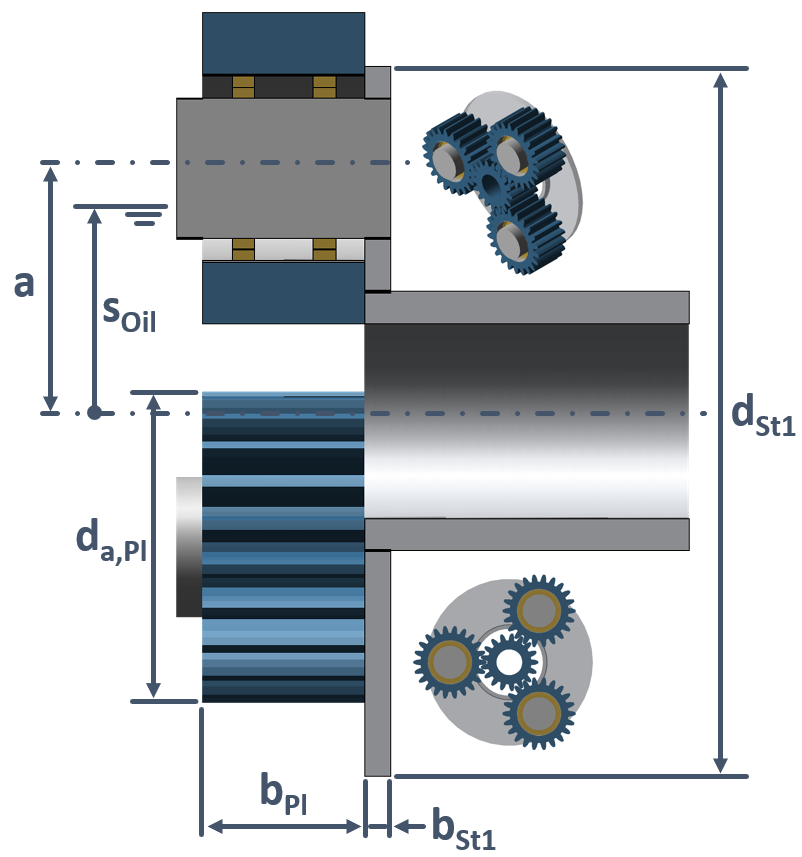Abbildung: Geometrische Daten des einwangigen Planetenradträgers

Zweiwangige Planetenträger nach KETTLER

Bei zweiwangigen geschlossenen Planetenträgern werden die Planschverluste ausschließlich vom im Öl planschenden Steg verursacht.

Gleichung 136.

P_{V S T, s w 2} = 4.6295 \cdot 10^{- 3} \cdot d_{S t 2}^{3.8} \cdot b_{S t 2} \cdot F_{e, S t 2}^{1.1945} \cdot n_{s 0}^{1.8559} \cdot ν_{O i l}^{0.22} \cdot ρ_{O i l}

Formelzeichen	Beschreibung	Einheit
P_VST,sw2	Planschverlustleistung der Stegwangen zweiwangiger Planetenradträger	W
d_St2	Gesamtdurchmesser des zweiwangigen Planetenradträgers	m
b_St2	Stegbreite des zweiwangigen Planetenradträgers	m
F_e,St2	Einflussfaktor Ölstand für Stegwangen von zweiwangigen Planetenradträgern	-
n_s0	Planetenradträgerdrehzahl	min^-1
ν_Oil	kinematische Betriebsölviskosität	mm²/s
ρ_Oil	Öldichte bei Betriebstemperatur	kg/m³

mit

Gleichung 137.

F_{e, S t 2} = 1

falls

Gleichung 138.

s_{O i l} > \frac{1}{2} \cdot d_{S t 2}

oder

Gleichung 139.

F_{e, S t 2} = \frac{1}{π} \cdot arccos (\frac{- 2 \cdot s_{O i l}}{d_{S t 2}})

falls

Gleichung 140.

s_{O i l} \leq \frac{1}{2} \cdot d_{S t 2}

und

Gleichung 141.

s_{O i l} \geq - \frac{1}{2} \cdot d_{S t 2}

oder

Gleichung 142.

F_{e, S t 2} = 0

falls

Gleichung 143.

s_{O i l} < - \frac{1}{2} \cdot d_{S t 2}

Formelzeichen	Beschreibung	Einheit
F_e,St2	Einflussfaktor Ölstand für Stegwangen von zweiwangigen Planetenradträgern	-
s_Oil	Ölstand bezogen auf die Getriebemitte	m
d_St2	Gesamtdurchmesser des zweiwangigen Planetenradträgers	m

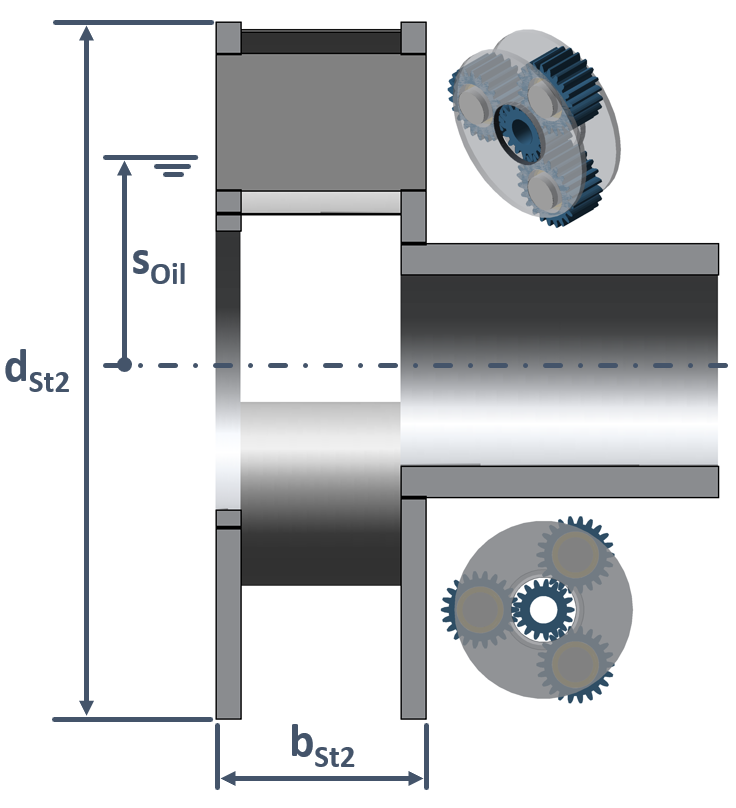Abbildung: Geometrische Daten des zweiwangigen Planetenradträgers

Dichtungsverluste

Die Verlustleistung durch Radial-Wellendichtringe entsteht aus der Reibung zwischen der meist feststehenden Dichtung und der rotierenden Welle. Diese Reibverluste hängen von verschiedenen Faktoren, wie Dichtungswerkstoff, Härte des Wellenwerkstoffes, Oberflächenrauhigkeit der Welle im Bereich der Dichtlippe, Schmierstoff und Temperatur an der Dichtstelle ab. Die Berechnung erfolgt durch vereinfachte empirisch ermittelte Formeln und Faktoren.

ISO 14179-1 (USA)

Die ISO/TR 14179-1 entspricht dem amerikanischen Ansatz der ISO zur Wärmehaushaltsberechnung von Getrieben. Darin enthalten ist die Berechnung der Dichtungsverluste basierend auf dem Regelwerk der Association for Rubber Products Manufacturers (ARPM OS-15).

Gleichung 144.

P_{V D} = \frac{T_{S} \cdot n}{9549}

mit

Gleichung 145.

T_{S} = 3.737 \cdot d_{s h}

falls VITON

Gleichung 146.

T_{S} = 2.429 \cdot d_{s h}

falls BUNA N

Formelzeichen	Beschreibung	Einheit
P_VD	Verlustleistung an der Dichtung	W
d_sh	Wellendurchmesser an der Dichtung	mm
n	Drehzahl der Welle relativ zur Dichtung	1/min

ISO 14179-2 (Deutschland)

Die ISO/TR 14179-2 ist der deutsche Ansatz der ISO zur Wärmehaushaltsberechnung von Getrieben. Darin enthalten ist die Berechnung der Dichtungsverluste basierend auf dem Katalog für Radialwellendichtungen der Firma Simrit/Freudenberg (SIMRIT).

Gleichung 147.

P_{V D} = 7.69 \cdot 10^{- 6} \cdot d_{s h}^{2} \cdot n

Formelzeichen	Beschreibung	Einheit
P_VD	Verlustleistung an der Dichtung	W
d_sh	Wellendurchmesser an der Dichtung	mm
n	Drehzahl der Welle relativ zur Dichtung	1/min

LINKE

Eine Erweiterung des Ansatzes aus der ISO 14179-2 zur Berechnung der Dichtungsverluste wird im Buch von Heinz Linke zur Stirnradverzahnung beschrieben (LINKE). Dieser Ansatz ergänzt die Berechnung um den Einfluss des Schmierstoffs bei unterschiedlichen Einsatztemperaturen.

Gleichung 148.

P_{V D} = [145 - 1.6 \cdot ϑ_{O i l} + 350 lg lg (ν_{40} + 0.8)] \cdot d_{s h}^{2} \cdot n \cdot 10^{- 7}

Formelzeichen	Beschreibung	Einheit
P_VD	Verlustleistung an der Dichtung	W
ϑ_Oil	Ölbetriebstemperatur	°C
ν₄₀	Kinematische Viskosität des Schmierstoffs bei 40°C	mm²/s
d_sh	Wellendurchmesser an der Dichtung	mm
n	Drehzahl der Welle relativ zur Dichtung	1/min

Quellen

Standards

ISO/TR 14179-1:2001(E): Gears - Part 1: Rating gear drives with thermal equilibrium at 95° C sump temperature, 2001
ISO/TR 14179-2:2001(E): Gears - Part 2: Thermal load-carrying capacity, 2001
DIN 3996:2019-09: Tragfähigkeitsberechnung von Zylinder-Schneckengetrieben mit sich rechtwinklig kreuzenden Achsen, 2019
DIN 31652-1:2017-01: Gleitlager; Hydrodynamische Radial-Gleitlager im stationären Betrieb - Teil 1: Berechnung von Kreiszylinderlagern, 2017
DIN 31653-1:1991-05: Gleitlager; Hydrodynamische Axial-Gleitlager im stationären Betrieb; Berechnung von Axialsegmentlagern, 1991
DIN 31654-1:1991-05: Gleitlager; Hydrodynamische Axial-Gleitlager im stationären Betrieb; Berechnung von Axial-Kippsegmentlagern, 1991
DIN 31657-1:1996-03: Gleitlager; Hydrodynamische Radial-Gleitlager im stationären Betrieb - Teil 1: Berechnung von Mehrflächen- und Kippsegmentlagern, 1996

Bücher, Kataloge, Anleitungen

SIMRIT: Radialwellendichtringe, Katalog Nr. 100, 1976
ESCHMANN, P. u. a.: Die Wälzlagerpraxis. Oldenburg München-Wien, 1978
NIEMANN, G., WINTER, H.: Maschinenelemente, Band 3, Berlin: Springer, 1983
FREUDENBERG: Simmering/Radial-Wellendichtringe, Katalog Nr. 100 Ausgabe 1/86
ARPM OS-15: Measuring Radial Lip Seal Torque and Power Consumption, Association for Rubber Products Manufacturers, 1986
LINKE, H.: Stirnradverzahnung, 2. Auflage, Carl Hanser Verlag München Wien, 2010
SKF: Rolling bearings, catalogue, PUB BU/P1 17000/1 EN, 2018
SCHAEFFLER: Rolling bearings, catalogue, HR 1, 2018
TIMKEN: Engineering manual bearings, catalogue, 2011
WTplus: FVA-EDV Programm WTplus, Version 2.2.1, Benutzeranleitung, 2016

Dissertationen und Publikationen

OHLENDORF, H.: Verlustleistung und Erwärmung von Stirnrädern, TH München, Diss., 1958
ARIURA, Y.: Lubricant churning loss in spur gear systems, JSME Vol. 16, pp. 881 -891, Veröffentlichung, 1973
WALTER, P.: Anwendungsgrenzen für die Tauchschmierung von Zahnradgetrieben, Plansch- und Quetschverluste bei Tauchschmierung, Universität Stuttgart, Diss., 1982
MAUZ, W.: Hydraulische Verluste bei Tauch- und Einspritzschmierung von Zahnradgetrieben, Universität Stuttgart, Diss., 1985
WECH, L.: Untersuchungen zum Wirkungsgrad von Kegelrad- und Hypoidgetrieben, TU München, Diss., 1987
BUTSCH, M.: Hydraulische Verluste schnelllaufender Stirnradgetriebe, Universität Stuttgart, Diss., 1989
SCHLENK, L.: Untersuchungen zur Fresstragfähigkeit von Großzahnrädern,TU München, Diss., 1995
BARTON, P. M.: Tragfähigkeit von Schraubrad- und Schneckengetrieben der Werkstoffpaarung Stahl/Kunststoff, Ruhr-Universität Bochum, Diss., 2000
DOLESCHEL, A.: Wirkungsgradberechnung von Zahnradgetrieben in Abhängigkeit vom Schmierstoff, TU München, Diss., 2002
WASSERMANN, J.: Einflussgrößen auf die Tragfähigkeit von Schraubradgetrieben der Werkstoffpaarung Stahl/Kunststoff, Ruhr-Universität Bochum, Diss., 2005
WIMMER, A.: Lastverluste von Stirnradverzahnungen - Konstruktive Einflüsse, Wirkungsgrad-maximierung, Tribologie, TU München, Diss., 2006
WENDT, T.: Tragfähigkeit von Schraubradgetrieben mit Schraubrädern aus Sintermetall, Ruhr-Universität Bochum, Diss., 2008
PECH, M.: Tragfähigkeit und Zahnverformung von Schraubradgetrieben der Werkstoffpaarungen Stahl/Kunststoff, Ruhr-Universität Bochum, Diss., 2011
MILTENOVIC, A.: Verschleißtragfähigkeitsberechnung von Schraubradgetrieben mit Schaubrädern aus Sintermetall, Ruhr-Universität Bochum, Diss., 2011
SUCKER, J.: Entwicklung eines Tragfähigkeitsberechnungsverfahrens für Schraubradgetriebe mit einer Schnecke aus Stahl und einem Rad aus Kunststoff, Ruhr-Universität Bochum, Diss., 2012

Forschungsvereinigung Antriebstechnik e.V. (FVA), Frankfurt/Main

MAUZ, W.: FVA-Heft 185: Zahnradschmierung-Leerlaufverluste, FVA Nr. 44 III, Abschlussbericht, 1985
MAURER, J.: FVA-Heft 432: Ventilationsverluste, FVA Nr. 44 VI, Abschlussbericht, 1994
SCHLENK, L.: FVA-Heft 443: Größeneinfluss Fressen, FVA-Nr. 166 I, Abschlussbericht, 1995
KETTLER, J.: FVA-Heft 639: Planetengetriebe-Sumpftemperatur, FVA-Nr. 313 I, Abschlussbericht, 2000
DOLESCHEL, A.: FVA-Heft 664: Wirkungsgradtest, FVA-Nr. 345 I, Abschlussbericht, 2001
GEIGER J.: FVA-Heft 959: Validierung WTplus, FVA-Nr. 69 V, Abschlussbericht, 2010
HAGEMANN, T.: FVA-Heft 996: Verbesserte Radialgleitlagerberechnung, FVA-Nr. 577 I, Abschlussbericht, 2011
PFEIFFER P.: FVA-Heft 1184: Radialkippsegmentlager Ölzuführungseinfluss, FVA-Nr. 677 I, Abschlussbericht, 2016
SEDLMAIR M.: FVA-Heft 1208: Erweiterung WTplus, FVA-Nr. 69 VI, Abschlussbericht, 2017
OEHLER, M.: FVA-Heft 1226: Schneckengetriebewirkungsgrade, FVA-Nr. 729 I, Abschlussbericht, 2017
JURKSCHAT, T.: FVA-Heft 1223: Verlustleistung von Stirnradverzahnungen, FVA-Nr. 686 I, Abschlussbericht, 2017
FINGERLE A.: FVA-Heft 1282: Durchgängige Berechnung gleitgelagerter Welle-Lager-Systeme, FVA-Nr. 668 II, Abschlussbericht, 2018
SEDLMAIR M.: FVA-Heft NA: Innenverzahnungen - Reibung und Wärme, FVA-Nr. 584 II, Projekt läuft aktuell noch, 2022

In diesem Abschnitt:

FVA-Workbench KnowledgeBase