Kegelräder - 3D-Neutraldaten

Die 3D-Neutraldatenschnittstelle zur diskreten Oberflächenbeschreibung ist eine Eingabeschnittstelle für BECAL, die die vollständige Beschreibung eines Radsatzes enthält. Sie ist sowohl für Kegel- und Hypoidradsätze (Bogenverzahnung, Geradverzahnung, Schrägverzahnung) als auch Beveloidverzahnungen und Stirnradverzahnungen verwendbar.

Diese Schnittstelle umfasst:

Grundgeometriegrößen
Relativlage der Zahnräder (beides in verkürzten Neutraldaten oder verkürzter Standard.KGD)
Vollständig mit Punkten beschriebene Zahn(oberflächen)geometrie (3D-Neutraldaten)

Grundgeometrie und Relativlage

Als Eingabedatei für die Grundgeometrie können sowohl verkürzte Neutraldaten gemäß der von Klingelnberg definierten Schnittstelle, als auch eine verkürzte Standard.KGD genutzt werden. Diese Eingabedatei(en) müssen folgende Informationen enthalten.

Zähnezahl, Normalmodul, Eingriffswinkel, Schrägungswinkel, Spiralrichtung
Zahnbreite, Zahnhöhe, Profilverschiebung, Zahndickenänderungsfaktor
Zahnberandung
Teil-, Kopf- und Fußkegel
Abstand zwischen Achskreuzungspunkt und Teil-, Kopf- bzw. Fußkegelspitze
Achsversatz, Achskreuzungswinkel

Der Eingabeblock $ BERANDUNG enthält den Polygonzug der Flankenberandung. Fehlt dieser Eingabeblock, so wird in BECAL der Polygonzug aus den folgenden Angaben berechnet:

Fußkegel, Kopfkegel, innerer und äußerer Ergänzungskegel
falls vorhanden unter Beachtung von:
- kegeliger Abdrehung an der Zehe (Breite und Kegelwinkel der Kopfkürzung) und
- zylindrischer Abdrehung an der Ferse (kopfgekürzter Durchmesser)

Jedwede Flankenberandungen werden einheitlich durch einen Polygonzug beschrieben. Sphärische Kopfberandungen können durch einen Polygonzug mit hinreichender Genauigkeit angenähert werden. Punkt 1 ist immer an Zehe-Fuß, Punkt 2 an Ferse Fuß, die folgenden laufen gegen den Uhrzeigersinn entlang der Kopfkante in Richtung Zehe.

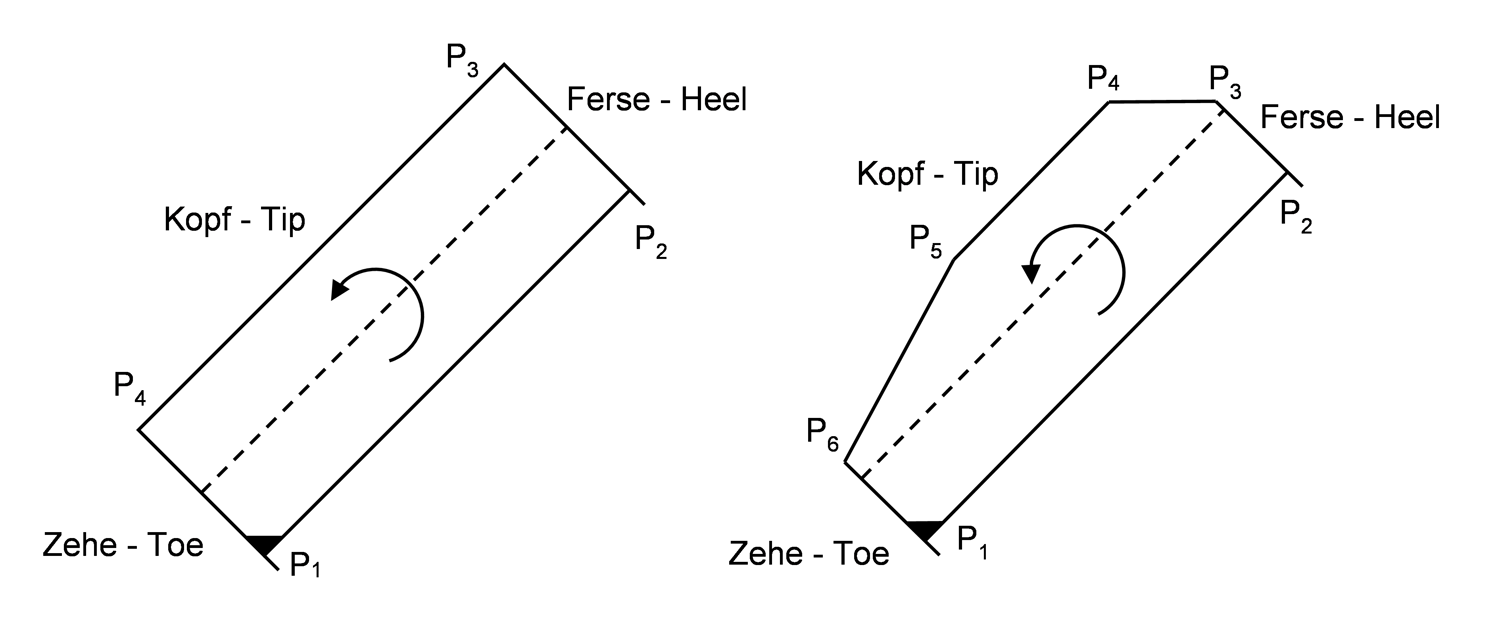
Beispiele für die Zahnberandung

Folgende weitere Eigenschaften muss der Polygonzug in der Standard.KGD erfüllen:

besteht aus mindestens 4 Punkten (zum Beispiel bei theoretischer Zahnberandung)
die Benennung der Punkte erfolgt gegen den Uhrzeigersinn (siehe Abbildung)
Punkt 1 beschreibt den inneren Punkt auf dem Fußkegel (Zehe)
Punkt 2 beschreibt den äußeren Punkt auf dem Fußkegel (Ferse)

Die folgende Darstellung zeigt den Block $ BERANDUNG einer Standard.KGD. In der ersten Zeile steht die Anzahl der Berandungspunkte für das jeweilige Rad. Danach folgen die Z- und R-Koordinaten der Punkte. Bei verschiedener Anzahl von Berandungspunkten für Ritzel und Rad ist das Prozentzeichen (%) der Platzhalter.

$ BERANDUNG
                  5                         4           Punktezahl
     60.59719     13.08327     21.71926     58.31119    Z, R( 1)
     85.73152     19.73649     28.37248     83.44552    Z, R( 2)
     83.67412     27.50888     20.60009     85.50292    Z, R( 3)
     62.65494     21.76898     13.94687     60.36859    Z, R( 4)
     58.53979     20.85566      %            %          Z, R( 5)

Der Eingabeblock $ MASCHINENEINSTELLUNGEN enthält die Spiralrichtung der gepaarten Räder. Für Geradverzahnungen wird festgelegt:

Ritzel bzw. Rad1: Spiralrichtung = 1
Tellerrad bzw. Rad2: Spiralrichtung = -1

Die Eingabeblöcke $ UEBERSETZUNGEN und $ SCHNEIDENGEOMETRIE enthalten Informationen, die nur für die Tragfähigkeitsberechnung relevant sind:

Wälz- oder Formverfahren, (1 … Wälzverfahren, 0 … Formverfahren)
Messerabrundungsradius am Werkzeug

Werden die Zahnräder nicht im Wälz- bzw. Formverfahren gefertigt, so sind die Eingabeblöcke $ UEBERSETZUNGEN und $ SCHNEIDENGEOMETRIE nicht in der verkürzten Standard.KGD enthalten. Fehlen diese Eingabeblöcke, werden diese Daten aus der Oberflächengeometrie berechnet.

Die folgenden Darstellungen enthält die Geometrie-Eingabeschnittstelle standard.kgd für eine Kegelradverzahnung, wenn zusätzlich eine Oberflächenbeschreibung in Form einer Punktewolke vorliegt.

Beispiel für eine verkürzte Standard.KGD für eine Kegelradverzahnung:

Klingelnbergv.- Datensatz fuer BECAL (intern)
            Ritzel                      RAD
     konvex         konkav       konvex        konkav 
$ GRUNDGEOMETRIE
                 35                        37           Zaehnezahl
            2.50001                   2.50001           mittl. Normalmodul
           10.00000                 -10.00000           mittl. Schraegungsw.
                         15.00000                       Achswinkel
                          0.00000                       Achsversatz
     20.00000     20.00000     20.00000     20.00000    Eingriffswinkel
            7.29047                   7.70953           Teilkegelwinkel
            7.29047                   7.70953           Kopfkegelwinkel
            7.29047                   7.70953           Fusskegelwinkel
            0.00000                   0.00000           Breite Kopfkuerz.
            0.00000                   0.00000           Kegelw. Kopfkuerz.
           95.32178                 100.24183           kopfgek. Durchmesser
          350.08059                 350.08059           mittl. Teilkegell.
           11.00000                  11.00000           Zahnbreite
            5.62502                   5.62502           Zahnhoehe
            0.02300                  -0.02341           Profilversch.-faktor
            0.02244                  -0.02956           Zahndickenaend.-faktor
            0.00000                   0.00000           Erzeugungsabstand
          -20.16188                 -18.19953           Kopfkegelabstand
           24.16467                  23.73100           Fusskegelabstand
$ BERANDUNG
                  4                         4           Punktezahl
    342.18399     40.68545    341.89297     43.07107    Z, R( 1)
    353.09506     42.08134    352.79351     44.54673    Z, R( 2)
    352.38126     47.66089    352.03891     50.12091    Z, R( 3)
    341.47018     46.26499    341.13836     48.64525    Z, R( 4)

$ MASCHINENEINSTELLUNGEN
                 -1                         1           Spiralrichtung
$ UEBERSETZUNGEN

            1            1            1            1    gewaelzt
$ SCHNEIDENGEOMETRIE



      0.75000      0.75000      0.75000      0.75000    Kopfradius (Messer)

Die Anzahl der Leerzeilen in diesen Blöcken ist einzuhalten, um eine Abwärtskompatibilität zu älteren BECAL-Projekten zu bewahren.

Zahnoberflächenbeschreibung mittels 3D-Neutraldaten-Dateien

Die Zahnoberflächenbeschreibung erfolgt über eine ASCII-Datei pro Rad, die punktweise die Nutzflanken, die Fußbereiche und die Übergangskurven von Nutzflanke und Fußbereich jeweils für die rechte und linke Zahnflanke beinhaltet. Außerdem sind für alle Punkte von Nutzflanke und Fußbereich die Normalenvektoren enthalten. Die Punkte zur Oberflächenbeschreibung liegen auf einem Gitter, das die gesamte Zahnoberfläche abdeckt. Die Lage von rechter und linker Flanke zueinander wird über den Zahndickenwinkel an einem definierten Gitterpunkt auf der Nutzflanke angegeben.

Prinzip-Skizze zu Punktegitter einer Zahnflanke

Die Flankengitterbeschreibung erfolgt für Tellerrad und Ritzel in zwei getrennten Dateien:

g_o___nm.dat
p_o___nm.dat

Diese ASCII-Dateien sind wie folgt aufgebaut:

Unterteilung in Kapitel (Reihenfolge der Kapitel in Datei beliebig).

obligatorische Kapitel:
- [general]
- [thickness]
- [flank right], [flank left]
- [rootradius right], [rootradius left]
- [fillet right], [fillet left]

Datenzeilen in den Kapiteln enthalten:
- Kennwort mit Gleichheitszeichen
- Zeichenkette: enthält Daten, die gemäß Kennwort interpretiert werden
- Kommentarzeilen beginnen mit comment
- zwischen den Kapiteln beliebig viele Leerzeilen möglich

Kapitel [general]

Das Kapitel [general] muss den Parameter spiri für die Spiralrichtung enthalten:

Rad rechtsgängig: spiri = 1
Rad linksgängig: spiri = -1

Für Geradverzahnungen wird festgelegt:

Ritzel bzw. Rad1: spiri = 1
Tellerrad bzw. Rad2: spiri = -1

[general]

ident=FVA-G44 9/34
date_time=08.01.2014 09:51
spiri=    1.00
version=  4.20

Kapitel [flank right] und [flank left]

Die Kapitel [flank right] bzw. [flank left] enthalten die Flankenpunkte der rechten bzw. linken Flanke in einem vorgegebenen Gitter. Die Gittergröße wird durch die Anzahl der Spalten rows und Zeilen lines angegeben. Danach folgen die Flankenpunkte und die dazugehörenden Normalenrichtungen:

Bezeichner aus Spaltennummer und Zeilennummer des Gitterpunktes
Zylinderkoordinaten: z, r, φ
Normalenvektor: n_z, n_r, n_φ

Folgende Regeln sind zu beachten:

Gleiche Spaltennummern in zueinander gehörenden Kapiteln [flank right], [rootradius right] und [fillet right] bzw. [flank left], [rootradius left] und [fillet left] beziehen sich immer auf ein und denselben Profilschnitt.
Die Anzahl der Spalten ist in allen oben genannten Kapiteln identisch.
Die Angabe der Punkte erfolgt innerhalb einer Profillinie vom Zahnkopf zum Fußbereich.

Lage des Werkrades im verwendeten Koordinatensystem:

Kegel- und Hypoidräder

Der Koordinatensystemursprung O ist der Achskreuzungspunkt im Getriebe.
Die z-Achse ist die Werkradachse.

Stirnradähnliche Verzahnungen

Der Koordinatensystemursprung OB wird über die Zahnbezugsebene festgelegt. (Die Zahnbezugsebene kann beliebig zwischen Zehe und Ferse des Rades gewählt werden.)
Die z-Achse ist die Werkradachse.

Definition der Koordinatensysteme

O_K - BECAL-Bezugssystem für Tellerrad und Ritzel mit Ursprung O_K

O_B - Bezugssystem für Beveloidräder mit Ursprung O_B

L_i - Einbaumaß für Beveloidräder (Abstand von Achskreuzungspunkt zu Zahnbezugsebene)

S_ti - Abstand der Teilkegelspitze zum Achskreuzungspunkt

Koordinatensysteme für die Flankenpunkte und die Normalenrichtung

Ein Flankenpunkt P wird im Koordinatensystem Σ = {O,e_x,e_y,e_z} durch die Zylinderkoordinaten (z,r,φ) beschrieben, wobei x = r⋅cos⁡(φ) und y = r⋅sin⁡(φ).
Der normierte Normalenvektor n im Punkt P wird im von P induzierten lokalen Koordinatensystem ΣP = {P,e_z,e_r,e_φ} durch seine kartesischen Komponenten (n_z,n_r,n_φ) beschrieben. Der Koordinatenursprung ist P, die r-Achse hat die entgegengesetzte Richtung wie das Lot von P auf die Werkradachse und die z-Achse hat die gleiche Richtung wie die z-Achse von Σ.

[flank right]
rows=   25
lines=  25
comment=        z_Soll           r_Soll        phi_Soll         nz            nr           nphi
00010001=    18.3880000000    64.7530394595 -0.0595882557 -0.3937065159  0.1901845697  0.8993469902
00010002=    18.6779000000    64.5568929891 -0.0570050932 -0.3878902292  0.1884217968  0.9022407642
00010003=    18.9679000000    64.3608306367 -0.0544587507 -0.3819185961  0.1865541169  0.9051716674
…
00250023=    39.3319000000    81.9767629800  0.0839853787 -0.5096971406 -0.1858177377  0.8400479708
00250024=    39.6219000000    81.7806623130  0.0855858112 -0.5046029116 -0.1901057366  0.8421613329
00250025=    39.9119000000    81.5845056276  0.0871859053 -0.5266101610 -0.1686012393  0.8332198752

[flank left]
rows=   25
lines=  25
comment=        z_Soll           r_Soll        phi_Soll         nz            nr           nphi
00010001=    18.3880000000    64.7530216553 -0.0121095564 -0.2655996122  0.2192825219 -0.9388141571
00010002=    18.6779000000    64.5568827169 -0.0140620255 -0.2581884992  0.2164994854 -0.9415235906
00010003=    18.9679000000    64.3607638461 -0.0159694937 -0.2505079387  0.2134200523 -0.9442974393
…
00250023=    39.3319000000    81.9767402478  0.0565447308  0.0685990146  0.5032808953 -0.8613956789
00250024=    39.6219000000    81.7806508442  0.0553727221  0.0306014161  0.5212085856 -0.8528805096
00250025=    39.9119000000    81.5845039505  0.0537539454 -0.0695967680  0.5665488334 -0.8210838625

Kapitel [rootradius right] und [rootradius left]

Die Kapitel [rootradius right] und [rootradius left] sind analog wie die Kapitel [flank right] und [flank left] aufgebaut. Sie enthalten die Koordinaten der Punkte im Fußbereich, die unmittelbar unterhalb des Flankengitters liegen und bis in den Fußgrund reichen. Die unteren Punkte des Flankengitters ([flank right], [flank left]) stimmen mit den oberen Punkten des Fußgitters ([rootradius right], [rootradius left]) überein.

[rootradius right]
rows=   25
lines=  16
comment=        z_Soll           r_Soll        phi_Soll         nz            nr           nphi
00010001=    25.3472000000    60.0468271017 -0.0082515842 -0.4188050885  0.2538255398  0.8718800910
00010002=    25.5034000000    59.9413076728 -0.0062931150 -0.4825105936  0.3040692159  0.8214167267
00010003=    25.6595000000    59.8356658848 -0.0038076775 -0.5616918864  0.3667291423  0.7416279127
…
00250014=    40.6366000000    81.0944484441  0.1001255091 -0.8360539389  0.5486470910 -0.0004251905
00250015=    40.6366000000    81.0944484441  0.1001255091 -0.8360539389  0.5486470910 -0.0004251905
00250016=    40.6366000000    81.0944484441  0.1001255091 -0.8360539389  0.5486470910 -0.0004251905

[rootradius left]
rows=   25
lines=  20
comment=        z_Soll           r_Soll        phi_Soll         nz            nr           nphi
00010001=    25.3472000000    60.0468765393 -0.0458068163 -0.3092965065  0.2688403657 -0.9121735190
00010002=    25.5034000000    59.9412645563 -0.0473803553 -0.3779973956  0.3159945468 -0.8702099835
00010003=    25.6595000000    59.8357119493 -0.0494170089 -0.4670979308  0.3759012714 -0.8003235328
…
00250018=    40.5994000000    81.1195876114  0.0372308276 -0.8380637168  0.5455718500  0.0007503694
00250019=    40.5994000000    81.1195876114  0.0372308276 -0.8380637168  0.5455718500  0.0007503694
00250020=    40.5994000000    81.1195876114  0.0372308276 -0.8380637168  0.5455718500  0.0007503694

Kapitel [fillet right] und [fillet left]

Die Kapitel [fillet right] und [fillet left] enthalten die Koordinaten von Punkten der Übergangskurve zwischen Nutzflankenbereich und Fußbereich. Die Gitterpunkte aus [fillet right] und [fillet left] bestehen immer nur aus einer Zeile pro Spalte, d. h. einem Punkt pro Profillinie.

[fillet right]
rows=   25
lines=   1
comment=        z_Soll           r_Soll        phi_Soll     C1
00010001=    24.6093000000    60.5458592627 -0.0139532297   1
00020001=    25.2526000000    61.4186122921 -0.0128413294   1
00030001=    25.8953000000    62.2917652536 -0.0114043934   1
…
00230001=    38.5728000000    79.8744507890  0.0730783730   1
00240001=    39.1949000000    80.7616145545  0.0797452457   1
00250001=    39.8154000000    81.6497803217  0.0866355460   1

[fillet left]
rows=   25
lines=   1
comment=        z_Soll           r_Soll        phi_Soll     C1
00010001=    24.2372000000    60.7975060883 -0.0404091737   1
00020001=    24.8859000000    61.6666062371 -0.0395321415   1
00030001=    25.5338000000    62.5362687433 -0.0383274054   1
…
00230001=    38.2185000000    80.1140680842  0.0426661262   1
00240001=    38.8395000000    81.0019320881  0.0492446183   1
00250001=    39.4590000000    81.8907507418  0.0560572452   1

In diesem Abschnitt:

FVA-Workbench KnowledgeBase