Cylindrical gear load carrying capacity

Standard load carrying capacity calculations

Standard load capacity calculations include the combined knowledge and experience of industry and research. They have been successfully applied in gear development for decades, and have been exhaustively validated.

These global methods use relatively simple formulas to determine comparative values; e.g., stresses, temperatures, and lubricating film thicknesses, which can be compared against permissible limit values.

To obtain reliable results, it is important that the manufacturing, materials, and the system and operating conditions are known as well as the geometric design of the gears. The more familiar you are with these specifications, the fewer the safeguards that need to be maintained, allowing for lighter, smaller, and more cost-effective gears.

Globally, there are a number of standard load capacity calculations for cylindrical gears. The most important international standard is surely ISO 6336. The latest edition was published at the end of 2019 and has been extensively revised. Additional important standards include DIN 3990 and AGMA 2101 D04.

In the FVA-Workbench, these calculations can be performed for the entire system as well as for individual stages. Standard calculations according to DIN, ISO, and AGMA can all be performed simultaneously.

ISO 6336 (International Organization for Standardization)

The International Organization for Standardization (ISO) is an international association of standards organizations (e.g.; DIN, ANSI, etc.). There are currently 164 countries represented in the ISO (121 full members, 39 corresponding members, and 4 observers).

There are 249 different Technical Committees (TC). TC 60 is focused on gears, and Sub Committee (SC) 2 deals with gear capacity calculation. Working Group (WG) 6 is concerned with gear calculations, including the cylindrical gears of ISO 6336 (ISO/TC 60/SC 2/WG 6 ).

For more information, refer to the ISO website at: https://www.iso.org.

Generally speaking, the application of standards is voluntary; standards are non-binding. Standards become legally binding when laws or legal regulations, such as EU directives, refer to them. Contractual partners may also specify the application of standards in their agreements.

ISO 6336:2019-11 "Calculation of load capacity of spur and helical gears" consists of the following parts:

Part 1:	Basic principles, introduction and general influence factors (replaces ISO 6336-1 Technical Corrigendum 1:2008-06, ISO 6336-1:2006-09)	ISO 6336-1:2019-11
Part 2:	Calculation of surface durability (pitting) (replaces ISO 6336-2 Technical Corrigendum 1:2008-06, ISO 6336-2:2006-09)	ISO 6336-2:2019-11
Part 3:	Calculation of tooth bending strength (replaces ISO 6336-3 Technical Corrigendum 1:2008-06, ISO 6336-3:2006-09)	ISO 6336-3:2019-11
Part 4:	Calculation of tooth flank fracture load capacity	ISO/TS 6336-4:2019-01
Part 5:	Strength and quality of materials	ISO 6336-5:2016-08
Part 6:	Calculation of service life under variable load (replaces ISO 6336-6 Technical Corrigendum 1:2007-08, ISO 6336-6:2006-08)	ISO 6336-6:2019-11
Part 20:	Calculation of scuffing load capacity - Flash temperature method (replaces ISO/TR 13989-1:2000-03)	ISO/TS 6336-20:2017-11
Part 21:	Calculation of scuffing load capacity - Integral temperature method (replaces ISO/TR 13989-2:2000-03)	ISO/TS 6336-21:2017-11
Part 22:	Calculation of micropitting load capacity (replaces ISO/TR 15144-1:2014-09)	ISO/TS 6336-22:2018-08
Part 30:	Calculation examples for the application of ISO 6336 parts 1,2,3,5	ISO/TR 6336-30:2017-11
Part 31:	Calculation examples of micropitting load capacity (replaces ISO/TR 15144-2:2014-10)	ISO/TR 6336-31:2018-09

ISO/TR – These "technical reports" contain purely informative data, e.g. example calculations.
ISO/TS – These "technical specifications" include calculation methods which are planned to be further developed and are intended to become a full-fledged standard.
ISO – These international standards include calculation methods that are based on widely accepted practices and have been extensively validated.

In the FVA-Workbench, ISO 6336 calculations can be performed for the entire system as well as individual components. Parts 1, 2, 3, and 6 make up the main part of the ISO. The following additional calculations can also be activated:

ISO 13691 - application standard for the petroleum and natural gas industries
DIN 3990 Part 4 - scuffing load capacity
ISO/TS 6336-20/-21:2017 - scuffing load capacity
FVA 166 - scuffing load capacity
FVA 54 - micropitting load capacity
IEC 61400-4:2012 - wind turbine gearboxes

ISO 6336-22 Calculation of micropitting load capacity

Calculation of the micropitting load capacity according to ISO/TS 6336-22:2018 supersedes the previous document, ISO/TR 15144-1:2014.The calculation method has been upgraded and integrated into the main ISO 6336 standard. The method was previously a technical report, a purely informative document. It is now a technical specification, meaning that the method is intended to be revised and transitioned into a complete standard.

Micropitting damage

Micropitting is fatigue damage on the contact surface of the mesh. It is a result of mixed friction due to an insufficient lubricating film thickness and the resulting breakdown of the surface. Visually, the damage can be identified by dull gray horizontal streaks across the face width. Under an electron microscope, a characteristic surface pattern can be recognized. With increasing operating time, material is removed from the area between the mesh and the pitch circle, similar to wear. The resulting profile form variation generally leads to increased meshing noise. Micropitting does not directly lead to gear failure, but it is often the beginning of consequential damage such as pitting.

Figure: micropitting

Micropitting resistance

This method calculates the safety against micropitting. To do so, the minimum specific lubricating film thickness on the path of contact is divided by the permissible specific lubricating film thickness.

Equation 152.

S_{λ} = \frac{λ_{G F, min}}{λ_{G F P}} \leq S_{λ, min}

Symbol	Description	Unit
S_λ	Safety against micropitting	-
λ_GF,min	Minimum specific lubricating film thickness on the path of contact	-
λ_GFP	Permissible specific lubricating film thickness	-
S_λ,min	Minimum required safety against micropitting	-

Equation 153.

λ_{G F, Y} = \frac{h_{Y}}{R a}

Equation 154.

h_{Y} = 1600 \cdot ρ_{n, Y} \cdot G_{M}^{0.6} \cdot U_{Y}^{0.7} \cdot W_{Y}^{- 0.13} \cdot S_{G F, Y}^{0.22}

Equation 155.

R a = 0.5 \cdot (R a_{1} + R a_{2})

Formula	Description	Unit
λ_GF,Y	Local specific lubricating film thickness on the path of contact at point Y	-
h_Y	Local lubricating film thickness at point Y	µm
ρ_n,Y	Normal radius of relative curvature at point Y	mm
G_M	Material factor, considers the influence of temperature on the modulus of elasticity and pressure-viscosity coefficient.	-
U_Y	Local velocity factor, describes the proportional increase of the specific lubricating film thickness with increasing dynamic viscosity of the lubricant at bulk temperature and the sum of the tangential velocities	-
W_Y	Local load factor, calculated from the local Hertzian contact pressure, taking the local factors and reduced modulus of elasticity into consideration	-
S_GF,Y	Local sliding factor, considers the influence of the local sliding on the local temperature. This temperature influences both the local pressure-viscosity coefficient and the local dynamic viscosity, and thus the local lubricating film thickness. The local contact temperature is the sum of the local flash temperature and the bulk temperature.	-
Ra	Effective arithmetic mean roughness value	µm
Ra_1/2	Arithmetic mean of the roughness value of the pinion/wheel	µm

The permissible specific lubricating film thickness can be determined using the methods from Annex A or B. The appendices, however, are purely informative and supportive, and are not part of the calculation method. Reference values are strongly recommended. Both annexes are only valid for mineral oils.

The calculation method in ISO/TS 6336-22:2018 is only valid for external cylindrical gears. The method can also be used for internal cylindrical gears, such as planetary stages, but the results do not deliver reliable values and should be used for informational purposes only.

For more details on the calculation, refer to ISO/TS 6336-22:2018.

Calculation in the FVA-Workbench

Only a few specifications are needed to complete the calculation according to ISO/TS 6336-22:2018.

The ISO 6336 calculation method must first be activated in the FVA-Workbench, the micropitting calculation can then be enabled under the ISO 6336 tab.

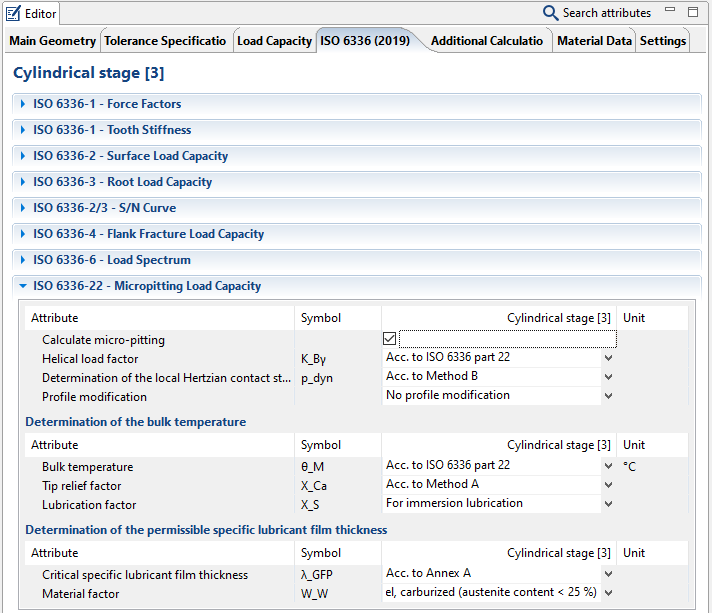Figure: The input attributes in the Editor have been reduced to a minimum. A detailed description of the individual attributes is available in the Attribute Help. The Attribute Help briefly describes the parameters and explains the input and selection options.

Calculation of the force factors is defined in the general section of ISO 6336-1. Only the helix angle factor is directly related to the micropitting calculation; therefore, it is also specified there.

In most cases, the calculation can be performed with the default settings.

The following points should be reviewed and adjusted if necessary:

Profile modification: The type and quality of the profile modification must be specified. For example, the user must decide whether the profile at the tip of the gear has been sufficiently corrected. This setting has a decisive influence on the load distribution, and thus on the contact pressure distribution and the lubricating film thickness over the path of contact.
Lubrication factor: The type of lubrication influences the bulk temperature of the gear, and therefore the local contact temperature, the lubricating and the material, and thus the lubricant film thickness.
Specific reference film thickness: The permissible minimum lubricating film thickness directly influences the safety against micropitting. Calculation according to Annex A and B is only valid for mineral oils and should be used with caution, as the properties of mineral oils can be significantly influenced by additives at any time. Therefore, reference tests are recommended to determine the minimum permissible lubricating film thickness for the specific application.

DIN 3990 (German Institute for Standardization)

DIN 3990 (1987) is the series of standards on the load capacity of cylindrical gears from the German Institute for Standardization (Deutsches Institut für Normung, DIN). The ISO 6336 (2006) series of standards is based on this standard. The DIN standard is currently being revised and updated. The new version will primarily be based on the new ISO 6336:2019-11.

In the FVA-Workbench, DIN 3990 calculations can be performed for the entire system or individual components. DIN consists of the following main parts:

DIN 3990-1: Introduction and general influence factors
DIN 3990-2: Calculation of pitting resistance
DIN 3990-3: Calculation of tooth strength
DIN 3990-4: Calculation of scuffing load capacity

The following additional calculations can also be activated:

FVA 54 - micropitting load capacity
FVA 166 - scuffing load capacity
Plewe (1980) - wear calculation

AGMA 2101 D04 (American Gear Manufacturers Association)

AGMA 2101 D04 is the American Gear Manufacturers Association (AGMA) series of standards for cylindrical gear design. The main standard is focused on gear tooth fracture and pitting damage. The following additional calculations can also be activated:

AGMA 6011 (I06) - Specification for High Speed Helical Gear Units
AGMA 6113 (A06) - Standard for Industrial Enclosed Gear Drives (Metric Edition)
AGMA 6114 (A06) - Gear Power Rating for Cylindrical Shell and Trunnion Supported Equipment (Metric Edition)
AGMA 925 (A03) - Effect of Lubrication on Gear Surface Distress
API 613 5th edition (February 2003) - Special Purpose Gear Units for Petroleum, Chemical, and Gas Industry Services
API 617 7th edition (July 2002) - Axial and Centrifugal Compressors and Expander-compressors

VDI 2736 (Association of German Engineers)

VDI 2736 Blatt 2 (2014) was issued by The Association of German Engineers (Verein Deutscher Ingenieure, VDI). It focuses on the calculation of the load-carrying capacity of thermoplastic gear wheels.

Old methods

In addition to the international and locally-recognized load capacity methods, there are many other local methods from different countries.

In the FVA-Workbench, the following three methods from older versions can still be used for calculations:

Load capacity according to BS 436 (1940)
This standard from the British Standards Institution (BSi) is entitled "Specification for machine cut gears. A. Helical and straight spur,“ and has been replaced by BS 436-1:1967, BS 436-2:1970, BS 436-3:1986.
Load capacity according to Niemann (1965)
Load capacity according to Henriot (1976)

Classification societies

Verification of the load capacity according to classification societies plays an important role for manufacturers of marine gear units and gears for the offshore industry. Most nations do not allow non-classified ships in their territorial waters.

There are currently twelve internationally recognized classification societies, which are grouped together under the umbrella organization International Association of Classification Societies (IACS). They all have different rulesets which must be complied with for classification.

The calculation of the load capacity for cylindrical gears is based on the International Organization for Standardization (ISO) standard with the designation ISO 6336 "calculation of load capacity of spur and helical gears." Until November 2019, ISO 6336 (2006) only covered the pitting and flank fracture forms of damage.

Classification society calculation guidelines are continually updated to include the latest findings from research and practice.

The recent publication of ISO 6336 in November 2019 means that an update to the classification society regulations is inevitable. Therefore, revised regulations should be expected in the next few years.

To facilitate recalculation for existing gears, it is still possible to perform calculations according to older and obsolete methods in the FVA-Workbench. For example, this may be necessary in the case of damage.

These calculations can only be performed for cylindrical gear stages, not the entire system. The influence of a complex system calculation with the resulting misalignment of the gear mesh and the effects of the microgeometry results in the face load factor K_Hβ. Once this has been determined, it can be specified for the single component calculation, thereby taking the behavior of the system into account.

The following classification societies are available in the FVA-Workbench:

American Bureau of Shipping (ABS), USA

The current ABS guideline "Rules for Building and Classing Steel Vessels" dates from 2019. Older ABS calculation methods from 1980, 2004, and 2011 are also still available in the FVA-Workbench.

The corresponding documents are available for download free of charge from the ABS homepage at https://ww2.eagle.org/.

The relevant section for cylindrical gears is Part 4, Chapter 3 "Propulsion and Maneuvering Machinery," Section 1, Appendix 1 "Rating of Cylindrical and Bevel Gears."

Basis of the ABS 2019 Calculation

Similar to ISO 6336, the following points are described in the standard:

Force factors

Symbol	Description
K_A	The application factor K_A accounts for dynamic overloads from sources external to the gearing. The application factor, for gears designed for infinite life is defined as the ratio between the maximum repetitive cyclic torque applied to the gear set and the nominal rated torque. The additional forces mainly depend on the characteristics of driving and driven machines, the masses and stiffnesses in the input and output trains (e.g. shafts and couplings), and the operating conditions.
K_γ	The load sharing factor K_γ accounts for the maldistribution of load in multiple-path transmissions; e.g., dual tandem, epicyclical, double helix. It is defined as the ratio between the maximum load through an actual path and the evenly shared load. The factor mainly depends on the accuracy and flexibility of the branches
K_v	The dynamic factor K_vaccounts for internally generated dynamic loads due to vibrations of the pinion and wheel against each other. The dynamic factor is defined as the ratio between the dynamic maximum force of a gear pair in mesh to the corresponding toothing forces of the same gear pair at a speed close to zero.
K_Hβ, K_Fβ	The face load distribution factors K_Hβ for contact stress and K_Fβ for tooth root bending stress account for the effects of non-uniform load distribution across the face width. The factors are defined as the ratio of the maximum load per unit face width to the mean load per unit face width.
K_Hα, K_Fα	The transverse load distribution factors K_Hα for contact stress and K_Fα for tooth root bending stress account for the effects of pitch and profile errors on the transverse load distribution between two or more pairs of teeth in mesh. The factors are defined as the ratio between the maximum force of a gear pair in mesh at a speed close to zero to the corresponding toothing forces of a deviation-free gear pair.

Flank load capacity

The criterion for surface durability is based on the Hertzian pressure on the operating pitch point or at the inner point of single pair contact. The contact stress σ_H is not to exceed the permissible contact stress σ_HP.

Contact stress σ_H

Equation 156.

σ_{H 1} = σ_{H 01} \cdot \sqrt{K_{A} \cdot K_{γ} \cdot K_{v} \cdot K_{H α} \cdot K_{H β}} \leq σ_{H P 1}

Equation 157.

σ_{H 2} = σ_{H 02} \cdot \sqrt{K_{A} \cdot K_{γ} \cdot K_{v} \cdot K_{H α} \cdot K_{H β}} \leq σ_{H P 2}

Equation 158.

σ_{H 01} = Z_{B} \cdot Z_{H} \cdot Z_{E} \cdot Z_{ε} \cdot Z_{β} \cdot \sqrt{\frac{F_{t}}{d_{1} \cdot b} \cdot \frac{u + 1}{u}}

Equation 159.

σ_{H 02} = Z_{D} \cdot Z_{H} \cdot Z_{E} \cdot Z_{ε} \cdot Z_{β} \cdot \sqrt{\frac{F_{t}}{d_{1} \cdot b} \cdot \frac{u + 1}{u}}

Symbol	Description	Unit
σ_H	Contact stress, for pinion and wheel in critical single pair contact	N/mm²
σ_H0	Basic value for contact stress at operating pitch point, the load on an error-free gear from the static rated torque, to be calculated separately for pinion and wheel	N/mm²
σ_HP	Permissible contact stress, to be calculated separately for pinion and wheel	N/mm²
Z_B	Single pair mesh factor for pinion, transforms the contact stresses determined at the pitch point to contact stresses considering the flank curvature at the inner point of single pair contact.	-
Z_D	Single pair mesh factor for wheel, transforms the contact stresses determined at the pitch point to contact stresses considering the flank curvature at the inner point of single pair contact.	-
Z_H	Zone factor, accounts for the influence on the Hertzian pressure of tooth flank curvature at pitch point and relates the tangential force at the reference cylinder to the normal force at the pitch cylinder	-
Z_E	Elasticity factor, accounts for the influence of the material properties modulus of elasticity and Poisson’s ratio	-
Z_ε	Contact ratio factor, accounts for the influence of the transverse contact ratio and the overlap ratio	-
Z_β	Helix angle factor, accounts for the influence of helix angle	-
F_t	Nominal transverse tangential load	N
b	Common face width	mm
d₁	Reference diameter of pinion	mm
u	Gear ratio = z₂ / z₁	-

Permissible contact stress σHP

Equation 160.

σ_{H P} = \frac{σ_{H lim}}{S_{H min}} \cdot Z_{N} \cdot Z_{L} \cdot Z_{V} \cdot Z_{R} \cdot Z_{W} \cdot Z_{X}

Symbol	Description	Unit
σ_HP	Permissible contact stress, to be calculated separately for pinion and wheel	N/mm²
σ_Hlim	Endurance limit for contact stress, accounts for the influence of the material, heat treatment, and surface of the standard reference test gear	N/mm²
S_Hmin	Required minimum safety factor for contact stress	-
Z_N	Life factor for contact stress, accounts for the higher permissible contact stress, including static stress, in case of a limited number of load cycles	-
Z_L	Lubricant factor, accounts for the influence of the type of lubricant and its viscosity	-
Z_V	Speed factor, accounts for the influence of the pitch line velocity	-
Z_R	Roughness factor, accounts for the influence of the surface roughness	-
Z_W	Hardness ratio factor, accounts for the increase of surface durability of a soft steel gear when meshing with a surface hardened gear with a smooth surface	-
Z_X	Size factor, accounts for the influence of tooth dimensions on permissible contact stress	-

If the gear is connected to the shaft by an interference fit, the permissible contact stress σ_HP is calculated by multiplying the factor K_S by the contact stress σ _H.

Equation 161.

K_{S} = 1 + \frac{δ_{max} \cdot 2.2 x 10^{5}}{Y} \cdot \frac{d_{r i}}{d_{w}^{2}} \cdot \frac{0.25 \cdot m_{n}}{ρ_{F s}}

Symbol	Description	Unit
K_S	Safety factor available for induced contact stresses	-
δ_max	Maximum available interference fit or maximum pull-up length	mm
d_ri	Inner diameter of wheel rim	mm
d_w	Working pitch diameter of wheel	mm
m_n	Normal module	mm
ρ_F	Root fillet radius in the critical section	mm
Y	Yield strength of wheel rim material	N/mm²

Tooth root bending strength

The criterion for tooth root bending strength is the permissible limit of local tensile strength in the root fillet. The tooth root stress σ_F and the permissible tooth root stress σ_FP are to be calculated separately for the pinion and the wheel, whereby σ_F is not to exceed the permissible tooth root stress σ_FP.

Tooth root stress σ_F

Equation 162.

σ_{F 1, 2} = \frac{F_{t}}{b \cdot m_{n}} \cdot Y_{F} \cdot Y_{S} \cdot Y_{β} \cdot K_{A} \cdot K_{γ} \cdot K_{v} \cdot K_{F α} \cdot K_{F β} \leq σ_{F P 1, 2}

Symbol	Description	Unit
σ_F	Tooth root stress, for pinion and wheel in critical single pair contact	N/mm²
σ_F0	Nominal tooth root stress, the maximum local tensile stress on an error-free gear from the static rated torque, to be calculated separately for pinion and wheel	N/mm²
σ_FP	Permissible tooth root stress, to be calculated separately for pinion and wheel	N/mm²
Y_F	Tooth form factor, represents the influence on nominal bending stress of the tooth form with load applied at the outer point of single pair tooth contact	-
Y_S	Stress correction factor converts the nominal bending stress to the local tooth root stress. Thereby, it includes the stress-increasing effect of the notch (fillet) and the fact that a complex stress state exists in the critical cross-section the root.	-
Y_β	Helix angle factor, converts the stress calculated for a point loaded cantilever beam representing the substitute gear tooth to the stress induced by a load along an oblique load line into a cantilever plate which represents a helical gear tooth.	-
F_t	Nominal transverse tangential load at reference cylinder	N
b	Face width	mm
m_n	Normal module	mm

Permissible tooth root stress σ_FP

Equation 163.

σ_{F P 1, 2} = \frac{σ_{F E}}{S_{F}} \cdot Y_{d} \cdot Y_{N} \cdot Y_{δ r e l T} \cdot Y_{R r e l T} \cdot Y_{X}

Symbol	Description	Unit
σ_FP	Permissible tooth root stress, to be calculated separately for pinion and wheel	N/mm²
σ_FE	Bending endurance limit, of the un-notched specimen, with the assumption that the material is fully elastic, including heat treatment.	N/mm²
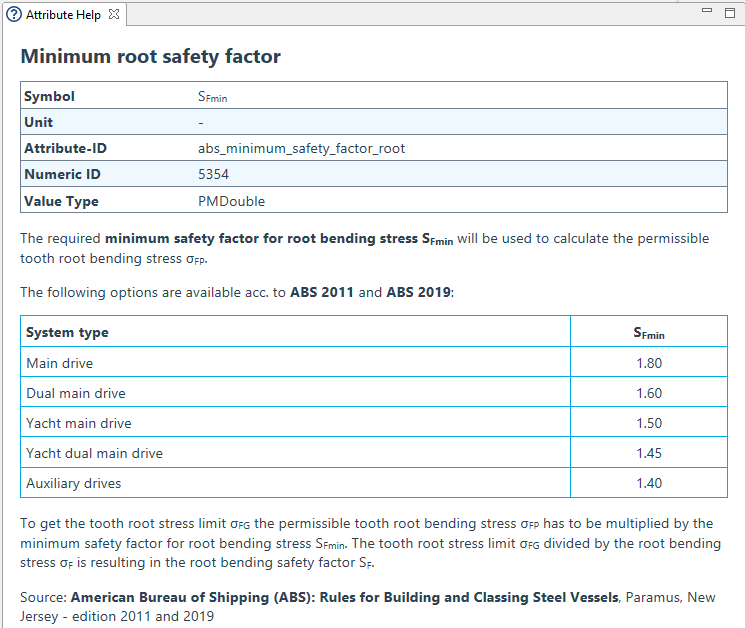
S_Fmin	Required minimum safety factor for tooth root bending stress	-
Y_d	Design factor, takes into account the influence of load reversing; i.e., for idler gears and gears with part load in reversed direction	-
Y_N	Life factor, accounts for the higher permissible tooth root bending stress in case of a limited life (number of load cycles)	-
Y_δrelT	Relative notch sensitivity factor, considers the influence of the notch sensitivity of the material	-
Y_RrelT	Relative surface factor, takes into account the dependence of the tooth root bending strength on the surface condition in the tooth root fillet	-
Y_X	Size factor (root), takes into account the decrease of the strength with increasing size	-

Calculations in the FVA-Workbench

Only a few attributes need to be specified for successful calculation according to ABS.

Input options

The input options for ABS 2019 are comparable to ABS 2011. Only a few points have been changed or expanded.

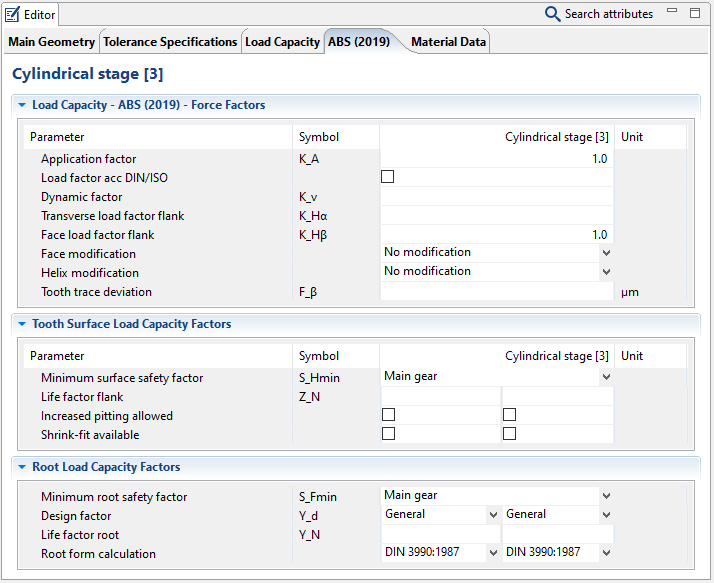
The ABS input attributes in the Editor are divided into three sections. A detailed description of the individual attributes is available in the Attribute Help. The Attribute Help briefly describes the parameters and explains the available input or selection options.

Force factors

These describe general external influences and system behavior. The factors are usually either directly specified or calculated according to the ABS rules or ISO6336.

Flank load capacity

Here, the critical point is the required minimum safety against pitting damage, which must be specified according to the application. The life factor, increased pitting, or an interference fit can optionally be defined to determine the permissible contact stress.

Tooth root bending strength

The required minimum safety against flank fracture must be specified according to the specific application. The design factor and life factor must be defined for calculation of the permissible tooth root stress. The root form geometry is decisive for calculation of the tooth root strength. According to ABS 2019, it is calculated as in DIN3990:1987. Optionally, the dedendum can also be calculated according to ISO6336:2006 and ISO6336:2019.

Bureau Veritas (BV), France

The latest version of the BV "Rules for the classification of steel ships" in the FVA-Workbench dates from 2010. In the FVA-Workbench, calculations can also still be performed according to BV rules from 1977 and 2003/2006.

The current rules can be downloaded for free from the BV homepage at https://www.bureauveritas.de/.

The relevant section for cylindrical gears is Part C "Machinery, Electricity, Automation, and Fire Protection," Chapter 1 "Machinery," Section 6 "Gearing."

A revised set of rules was published in January 2020; however, this has not yet been implemented in the FVA-Workbench. One particular feature of this version is that it also includes calculation of the scuffing load capacity according to the flash temperature method.

China Classification Society (CCS), China

The latest CCS "Rules for classification of sea-going steel ships" in the FVA-Workbench dates to 1996.

The relevant section for cylindrical gears is Part 3, Chapter 10 "Transmission gearing," Appendix 1 "Appraisal of gear strength."

The current rules can be downloaded free of charge from the CCS homepage at https://www.ccs.org.cn/.

Det Norske Veritas (DNV), Norway

DNV merged with Germanischer Lloyd (GL) from Germany in 2013. Therefore, there are no updated DNV rulebooks since this date.

The most recent DNV "Calculation of Gear Rating for Marine Transmissions N.41.2“ in the FVA-Workbench is from 2012. In the FVA-Workbench, calculations can also still be performed according to DNV rules from 1978, 1990/1993, and 2003.

One particular feature of this version is that it also includes calculation of the scuffing load capacity according to the flash temperature method.

The current rules can be downloaded for free from the DNV-GL homepage at https://www.dnvgl.de/.

Germanischer Lloyd (GL), Germany

GL merged with Det Norske Veritas (DNV) from Norway in 2013. Therefore, there are no updated GL rulebooks since this date.

The most recent GL "Rules for Classification and Construction - Ship Technology" in the FVA-Workbench is from 1998/2006. In the FVA-Workbench, calculations can also still be performed according to an older GL method from 1980.

The relevant section for cylindrical gears is Part 1 "Seagoing Ships," Chapter 2 "Machinery Installations," Section 5 "Gears, Couplings."

The current rules can be downloaded for free from the DNV-GL homepage at https://www.dnvgl.de/ .

Lloyd's Register of Shipping (LRS), England

The latest LRS "Rules and Regulations for the Classification of Ships" in the FVA-Workbench is from 2019. In the FVA-Workbench, calculations can also be performed according to LRS methods from 1978 and 1990/2006.

The relevant section for cylindrical gears is Part 5 "Main and Auxiliary Machinery," Chapter 5, "Gearing," Section 3, "Design."

The current rules can be downloaded free of charge from the LRS homepage at https://www.lr.org/.

Registro Italiano Navale (RINA), Italy

The current version of the RINA "Rules for the classification of ships" in the FVA-Workbench is from 2004/2006. In the FVA-Workbench, calculations can also still be performed according to an older RINA method from 1982.

The relevant section for cylindrical gears is Part C "Machinery, Systems and Fire Protection," Chapter 1 "Machinery," Section 6 "Gearing."

The current rules can be downloaded free of charge from the RINA homepage at https://www.rina.org/.

Russian Maritime Register of Shipping (RMS), Russia

The current version of the RMS "Rules for the Classification and Construction of Sea-Going Ships" in the FVA-Workbench is from 2005/2020.

The relevant section for cylindrical gears is Part IX "Machinery," Chapter 4 "Gears, disengaging and elastic couplings," Section 2 "Gearing."

The current rules can be downloaded free of charge from the RMS homepage at https://rs-class.org/.

In this section:

KnowledgeBase