Power loss

Power losses and efficiency calculation in the FVA-Workbench

Equation 1.

P_{V} = (P_{V Z P} + P_{V Z 0}) + (P_{V L P} + P_{V L 0}) + P_{V P B} + P_{V D} + P_{V S T} + P_{V X}

Symbol	Description	Unit
P_V	Total power loss	W
P_VZP	Load-dependent gear losses	W
P_VZ0	Load-independent gear losses	W
P_VLP	Load-dependent rolling bearing losses	W
P_VL0	Load-independent rolling bearing losses	W
P_VPB	Plain bearing losses	W
P_VD	Sealing losses	W
P_VST	Rim or planet carrier losses	W
P_VX	Other losses	W

Power losses caused by tooth and bearing friction can be divided into load-dependent (index 0) and load-independent (index P) power losses.

Seals, bearings, and gears have a negative effect on the overall efficiency due to rolling and sliding friction, even without load.

The following table lists the different calculation approaches for various components, including the corresponding methods/sources.

Type of loss	Components	Method/source
P_VZP	Cylindrical gears	H_v according to OHLENDORF, TALBOOM, WIMMER µ_mZ according to SCHLENK, DOLESCHEL
P_VZP	Bevel and hypoid gears	H_V and µ_mZ according to WECH
P_VZP	Worm stages	DIN 3996, FVA 729 I
P_VZ0	Cylindrical gears, bevel and hypoid gears	Splash lubrication: Squeeze and splash losses according to MAUZ, WALTER Injection lubrication: Squeeze losses according to MAUZ, BUTSCH Pulse losses according to ARIURA, BUTSCH Ventilation losses according to MAURER
P_VLP,P_VL0	Rolling bearings	SKF, SCHAEFFLER, TIMKEN, ISO14179-2
P_VPB	Plain bearings	COMBROS R&A
P_VD	Seals	ISO 14179-1, ISO 14179-2, LINKE
P_VST	Planet carriers	KETTLER

Table: Power loss calculations, methods, sources

The losses are considered in the system calculation. Torque losses are subtracted from the transferred torque at the position in the power flow at which they occur. The speed remains unaffected; the losses do not have a braking or slowing effect on the overall system.

The efficiency of the gearbox is calculated from the ratio of useable power to applied power.

Equation 2.

η = \frac{P_{A n} - P_{V}}{P_{A n}} \cdot 100

Symbol	Description	Unit
η	Efficiency	%
P_An	Input power	W
P_V	Total power loss	W

Gear losses

The power loss of the gears is calculated from the load-dependent and load-independent loss components. The calculation differentiates between cylindrical gears, bevel and hypoid gears, and worm gears.

Load-dependent gear losses for cylindrical gears

The load-dependent gear losses are determined using the following basic equation, based on Coulomb friction.

Equation 3.

P_{V Z P} = H_{V} \cdot μ_{m Z} \cdot P_{A n}

Symbol	Description	Unit
P_VZP	Load-dependent gear losses	W
H_V	Tooth loss factor	-
µ_mZ	Average gear friction coefficient	-
P_An	Input power	W

There are different methods for calculating the tooth loss factor and average gear friction coefficient. These are described in more detail below.

Tooth loss factor according to OHLENDORF

The tooth loss factor according to OHLENDORF is very often used to evaluate the efficiency of the geometric design of a gear. The method shown here corresponds to the generally accepted extension according to Wimmer.

Equation 4.

H_{V} = \frac{π \cdot (u + 1)}{z_{1} \cdot u \cdot cos β_{b}} \cdot (a_{0} + a_{1} | ϵ_{1} | + a_{2} | ϵ_{2} | + a_{3} | ϵ_{1} | ϵ_{1} + a_{4} | ϵ_{2} | ϵ_{2})

Symbol	Description	Unit
H_V	Tooth loss factor	-
u	Gear ratio (z₂/z₁)	-
z_1/2	Number of teeth of pinion/wheel	-
β_b	Base circle helix angle	deg
ε_1/2	Tip contact ratio of pinion/wheel	-
a_0…4	Coefficients for tooth loss factor	-

With coefficients for the tooth loss factor from:

Transverse contact ratio	Location of the pitch point C	a ₀	a ₁	a ₂	a ₃	a ₄
0 ≤ ε_α ≤ 1	before the engagement area	0	0	0	1/ε_α	1/ε_α
	in the engagement area	0	0	0	1/ε_α	1/ε_α
	after the engagement area	0	0	0	1/ε_α	1/ε_α
1 < ε_α ≤ 2	before the engagement area	0	1	1	0	0
	in the first double engagement area	0	1	-1	0	1
	in the engagement area	1	-1	-1	1	1
	in the second double engagement area	0	-1	1	1	0
	after the engagement area	0	1	1	0	0
2 < ε_α ≤3	before the engagement area	0	1	1	0	0
	in the first triple engagement area	0	1	-1	0	2/3
	in the first double engagement area	4/3	-1/3	-1	1/3	2/3
	in the second triple engagement area	1	-1/3	-1/3	1/3	1/3
	in the second double engagement area	4/3	-1	-1/3	2/3	1/3
	in the third triple engagement area	0	-1	1	2/3	0
	after the engagement area	0	1	1	0	0

Tooth loss factor according to TALBOOM

The TALBOOM method is a ZF company standard.

Equation 5.

H_{V} = \frac{π \cdot (\frac{1}{z_{1}} + \frac{1}{z_{2}})}{cos β_{b}} \cdot 0.9 \cdot ϵ_{1}^{2} + 1.1 \cdot ϵ_{2}^{2} - (0.9 \cdot ϵ_{1} + 1.1 \cdot ϵ_{2}) \cdot (ϵ_{α} - 1) + \frac{2}{3} \cdot {(ϵ_{α} - 1)}^{2}

This formula is applicable when the first gear is the driving gear; otherwise, the tip contact ratios in the formula are changed to the other gear, accordingly.

Symbol	Description	Unit
H_V	Tooth loss factor	-
z_1/2	Number of teeth of pinion/wheel	-
β_b	Base circle helix angle	deg
ε_1/2	Tip contact ratio of pinion/wheel	-
ε_α	Transverse contact ratio	-

Local-geometric tooth loss factor according to WIMMER

The local-geometric tooth loss factor according to WIMMER considers the actual load distribution, including gear modifications. Efficiency is improved when the load is shifted in the direction of the pitch point in tooth contact. As a result, this method can be used for efficiency-oriented gear design.

In the Ohlendorf calculation, the tooth contact is only considered on the path of contact, and a simplified formula is derived based on assumptions. The basic equation is:

Equation 6.

H_{V} = \frac{1}{p_{e t}} \cdot \int_{x = A}^{E} F_{N} (x) \cdot v_{g} (x) d x

The Wimmer calculation also considers the contact width, and the tooth loss factor is calculated using numerical methods without simplifications. The starting point is the following equation:

Equation 7.

H_{V} = \frac{1}{p_{e t}} \cdot \int_{y = 0}^{b} \int_{x = A}^{E} \frac{F_{N} (x, y)}{F_{b t}} \cdot \frac{v_{g} (x, y)}{v_{t b}} d x d y

Symbol	Description	Unit
H_V	Tooth loss factor	-
p_et	Base pitch at base circle	mm
x	Coordinates on the path of contact: distance from the pitch point	mm
A,E	Coordinates on the path of contact: beginning and end of the path of contact	mm
F_N	Normal force of the tooth	N
v_g	Sliding speed	m/s
y	Coordinate on the path of contact	mm
b	Face width of the contact	mm
F_bt	Peripheral force at pitch circle	N
v_tb	Circumferential speed at base circle	m/s

Average gear friction coefficient according to SCHLENK

The SCHLENK method is most commonly used for calculating the average gear friction coefficient. Only a few input variables are required.

Equation 8.

μ_{m Z} = 0.048 \cdot {(\frac{F_{b t} / b}{v_{Σ C} \cdot ρ_{r e d C}})}^{0.2} \cdot η_{O i l}^{- 0.05} \cdot R a^{0.25} \cdot X_{L}

Symbol	Description	Unit
µ_mZ	Average tooth friction coefficient	-
F_bt	Peripheral force at pitch circle	N
v_ΣC	Sum of speeds at pitch point	m/s
ρ_redC	Equivalent radius of curvature at pitch point	mm
η_Oil	Dynamic operating oil viscosity	mPas
X_L	Lubricant factor	-
Ra	Arithmetic mean roughness value of the gear partners 0.5 · (Ra₁ + Ra₂)	µm
b	Face width	mm

Average gear friction coefficient according to DOLESCHEL

The DOLESCHEL method is more accurate than the simple SCHLENK method for determining the average gear friction coefficient. However, it requires specific test rig reference measurements that are often not available in practice.

Equation 9.

μ_{m Z} = (1 - ξ) \cdot μ_{F} + ξ \cdot μ_{E H D}

with

Equation 10.

ξ ∊ [0; 1]

and

Equation 11.

μ_{E H D} = μ_{E H D, r e f} \cdot {(\frac{p_{H}}{p_{H, r e f}})}^{α_{E H D}} \cdot {(\frac{v_{Σ}}{v_{Σ, r e f}})}^{β_{Σ, E H D}} \cdot {(\frac{η_{O i l}}{η_{O i l, r e f}})}^{γ_{E H D}}

Equation 12.

μ_{F} = μ_{F, r e f} \cdot {(\frac{p_{H}}{p_{H, r e f}})}^{α_{F}} \cdot {(\frac{v_{Σ}}{v_{Σ, r e f}})}^{β_{Σ, F}}

with

Equation 13.

ξ = 1 - {(1 - (0.5 \cdot \frac{h_{0}}{R a}))}^{2}

Equation 14.

h_{0} \leq 2 \cdot R a

Equation 15.

ξ = 1

where

Equation 16.

h_{0} > 2 \cdot R a

Symbol	Description	Unit
µ_mZ	Average tooth friction coefficient	-
ξ	Amount of EHD friction for mixed friction	-
µ_F,ref	Solid friction coefficient (under reference conditions)	-
µ_EHD,ref	EHD friction coefficient (under reference conditions)	-
p_H,ref	Hertzian contact stress (under reference conditions)	MPa
v_Σ,ref	Sum of speeds (under reference conditions)	m/s
η_Oil,ref	Dynamic operating oil viscosity (under reference conditions)	mPas
α_EHD/F	Exponent for pressure influence	-
β_Σ,EHD/F	Exponent for sum of speeds influence	-
γ_EHD	Exponent for viscosity influence	-
h₀	Minimum lubricating film thickness	µm
Ra	Arithmetic mean roughness value of the gear partners 0.5 · (Ra₁ + Ra₂)	µm

These 11 test rig reference measurements must be specified for the lubricant in the database.

Load-dependent gear losses for bevel/hypoid gears

The load-dependent gear losses of bevel and hypoid gears are managed similar to cylindrical gears. The WECH calculation method is used. This method approximates bevel and hypoid gears as virtual crossed helical gears according to Niemann/Winter.

The gear losses are calculated from the average friction coefficient, the tooth loss factor, and the input power:

Equation 17.

P_{V Z P} = μ_{m Z} \cdot H_{V} \cdot P_{A n}

Symbol	Description	Unit
P_VZP	Load-dependent gear losses	W
µ_mZ	Average gear friction coefficient	-
H_V	Tooth loss factor	-
P_An	Input power	W

The following factors have an influence on the average friction coefficient µ_mZ:

The load, average total sliding speed, and the average sum of speeds of the virtual crossed helical gear and the equivalent radius of curvature at the pitch point are considered via the load and geometry factor Q_H.
The lubricant characteristics V_L, type of lubrication V_S, operating oil viscosity V_Z, and roughness of the tooth flanks V_R are included as factors.

Equation 18.

μ_{m Z} = 0.054 \cdot V_{R} \cdot V_{S} \cdot V_{Z} \cdot V_{L} \cdot Q_{H}

Symbol	Description	Unit
µ_mZ	Average gear friction coefficient	-
V_R	Roughness factor	-
V_S	Lubrication factor	-
V_Z	Viscosity factor	-
V_L	Lubricant factor	-
Q_H	Load and geometry factor	-

Equation 19.

Q_{H} = \frac{{(F_{N} \cdot \frac{cos β_{b 2}}{b_{2}})}^{0.05}}{K_{g m}^{0.6} \cdot ρ_{n}^{0.2} \cdot v_{Σ m}^{0.35}}

Symbol	Description	Unit
Q_H	Load and geometry factor	-
F_N	Normal force of the virtual gear	N
β_b2	Helix angle at base circle of gear	deg
b₂	Face width of gear	m
K_gm	Sliding factor	-
ρ_n	Equivalent radius of curvature	m
v_Σm	Mean sum of velocity	m/s

If it is already known (for example, either internally confirmed or from tests), the coefficient of friction can also be specified as an input value instead of calculated according to WECH.

The tooth loss factor H_V is also calculated according to WECH for the virtual crossed helical gears, and considers its load sharing and speed course over the path of contact. The calculation is finally performed by integrating the speed course over the path of contact.

For more detailed information on the calculation, refer to the Wech dissertation (in German):

WECH, L.: Untersuchungen zum Wirkungsgrad von Kegelrad- und Hypoidgetrieben, TU München, Diss., 1987

Load-dependent gear losses for worm gear stages

The load-dependent gear losses of worm gear stages are calculated according to DIN 3996.

For the driving worm gear:

Equation 20.

P_{V Z P} = P_{A n} \cdot (1 - η_{Z})

with

Equation 21.

η_{Z} = \frac{tan (γ_{m})}{tan (γ_{m}) + arctan (μ_{m Z})}

For the driven worm gear:

Equation 22.

P_{V Z P} = P_{A n} \cdot (1 - η_{Z}^{*})

with

Equation 23.

η_{Z}^{*=} \frac{tan (γ_{m}) - arctan (μ_{m Z})}{tan (γ_{m})}

Symbol	Description	Unit
P_VZP	Load-dependent gear losses	W
P_An	Input power	W
η_Z	Gear efficiency	-
γ_m	Reference lead angle	deg
µ_mZ	Average gear friction coefficient	-

There are different methods for calculating the average gear friction coefficient. They are described in more detail below.

Average gear friction coefficient according to DIN 3996:2019

Calculation of the average gear friction coefficient according to the Oehler dissertation (2018) was integrated into the 2019 revision of DIN 3996. Part of the work for this dissertation was performed within FVA Research Project 729 I, and is documented in the final report (2017).

The average gear friction coefficient is calculated as follows:

Equation 24.

μ_{m Z} = Ψ \cdot μ_{G r} + (1 - Ψ) \cdot μ_{F l}

Symbol	Description	Unit
µ_mZ	Average gear friction coefficient	-
µ_Gr	Boundary friction coefficient	-
µ_Fl	Liquid friction coefficient	-
Ψ	Solid load bearing amount	-

The boundary friction coefficient depends on the type of base oil, the average flank pressure, as well as the material of the worm and worm gear.

The solid load bearing amount depends on the average minimum lubrication gap thickness, the surface topography of the worm and gear flanks, and their materials.

The liquid friction coefficient is calculated from the average shear stress in the lubrication gap, average flank pressure, and the solid load bearing amount.

Average gear friction coefficient according to DIN 3996:2012

Even though the standard is no longer valid, the average gear friction coefficient can still be calculated according to DIN 3996:2012 for comparison purposes.

The associated formula is as follows:

Equation 25.

μ_{m Z} = μ_{0 T} \cdot Y_{S} \cdot Y_{G} \cdot Y_{W} \cdot Y_{R}

Symbol	Description	Unit
µ_mZ	Average gear friction coefficient	-
µ_0T	Basic friction coefficient	-
Y_S	Size factor	-
Y_G	Geometry factor	-
Y_W	Material factor	-
Y_R	Roughness factor	-

Load-independent gear losses for cylindrical, bevel, and hypoid gears

No-load gear losses include splash, squeeze, ventilation, and pulse losses. These losses are speed-dependent but not load-dependent. Load-independent gear losses are typically much smaller than load-dependent gear losses.

Load-independent gear losses can be calculated according to various methods, depending on the type of lubrication and the circumferential speed.

Immersion lubrication

Squeeze and splash losses are considered with immersion lubrication.

Equation 26.

P_{V Z 0, t a u c h} = P_{V Z 0, q u e t s c h} + P_{V Z 0, p l a n s c h}

Symbol	Description	Unit
P_VZ0,tauch	Load-independent gear losses with immersion lubrication	W
P_VZ0,quetsch	Squeeze losses: squeezing out of excess oil in the tooth contact	W
P_VZ0,plansch	Splash losses: splashing of the gears in the oil	W

Whether the squeeze and splash losses should be determined according to MAUZ or WALTER can be specified individually for all cylindrical gear stages. The default is calculation according to MAUZ. Detailed warnings will be issued if the validity range of the MAUZ or WALTER calculation equations are exceeded; however, the calculation will continue if possible.

Load-independent gear losses with immersion lubrication according to MAUZ

The entire hydraulic torque losses (i.e., the sum of the squeeze and splash torque losses) are transferred to the pinion or wheel shaft, depending on the load path.

Transferred to the pinion shaft:

Equation 27.

T_{V Z 0, t a u c h} = (T_{V Z 0, p l a n s c h, R i t z e l} + \frac{z_{1}}{z_{2}} \cdot T_{V Z 0, p l a n s c h, R a d}) \cdot K_{P 1 G} + T_{V Z 0, q u e t s c h}

Transferred to the wheel shaft:

Equation 28.

T_{V Z 0, t a u c h} = (T_{V Z 0, p l a n s c h, R i t z e l} \cdot \frac{z_{2}}{z_{1}} + T_{V Z 0, p l a n s c h, R a d}) \cdot K_{P 1 G} + T_{V Z 0, q u e t s c h}

Symbol	Description	Unit
T_VZ0,tauch	Load-independent gear torque loss with immersion lubrication	Nm
T_VZ0,quetsch	Squeeze torque losses	Nm
T_{VZ0,plansch,Ritzel/Rad}	Splash torque loss of the pinion/wheel	Nm
K_P1G	Correction factor for the simultaneously immersed mating gear	-
z_1/2	Number of teeth of the pinion/wheel	-

The power loss is calculated according to the reference shaft with the following formula:

Equation 29.

P_{V Z 0} = T_{V Z 0, t a u c h} \cdot 2 \cdot π \cdot n

Symbol	Description	Unit
P_VZ0,tauch	Load-independent gear losses with immersion lubrication	W
T_VZ0,tauch	Load-independent gear torque loss with immersion lubrication	Nm
n	Shaft speed	1/s

Squeeze losses according to MAUZ

Different operating cases are considered in the squeeze losses according to MAUZ.

If both shafts are arranged horizontally and the immersed gear feeds the oil:

directly into the tooth mesh, case W1
indirectly into the tooth mesh via the wall of the casing, case W2

If the shafts are arranged vertically, the direction of rotation is inconsequential. This corresponds to cases S1 and S2.

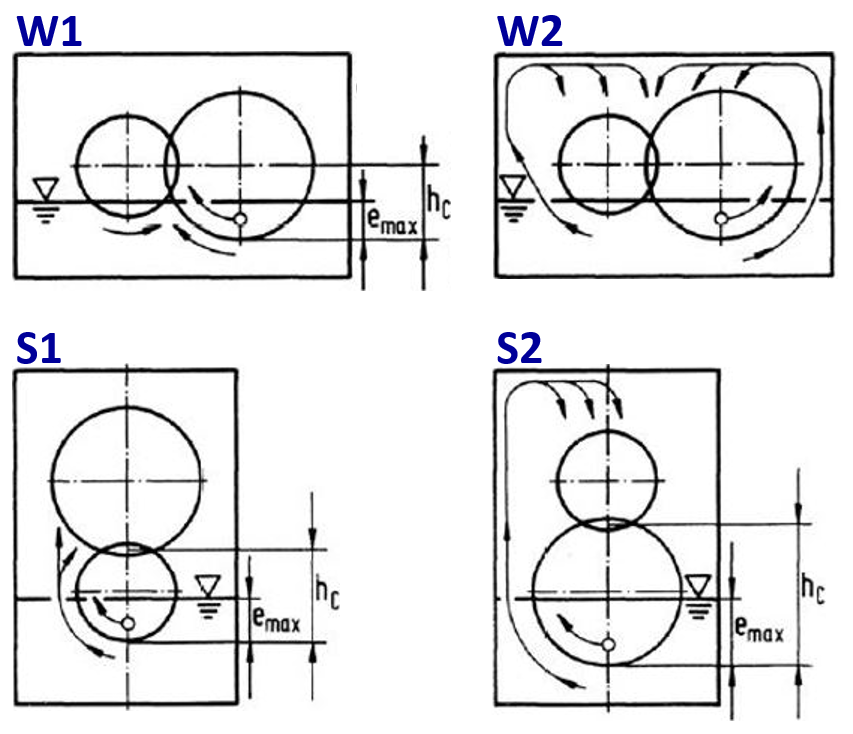Figure: operating cases

The squeeze torque loss of the mesh is calculated as:

Equation 30.

T_{V Z 0, q u e t s c h} = 0.0235 \cdot ρ_{O i l} \cdot b \cdot r_{w} \cdot v_{t}^{1.2} \cdot C_{S p}

where

Operating case W1: C_Sp = e/h_c
Operating case W2: C_Sp = 0
Operating cases S1 and S2: C_Sp = (e/h_c)²

Symbol	Description	Unit
T_VZ0,quetsch	Squeeze torque loss	Nm
ρ_Oil	Oil density at operating temperature	kg/m³
b	Minimum face width of pinion and wheel	m
r_w	Radius at pitch circle of the deepest immersed gear	m
v_t	Circumferential speed at pitch circle	m/s
C_Sp	Splash oil factor	-
e	Immersion depth of the deepest immersed gear	mm
h_c	Height of the point of contact above the point of deepest immersion of the cylindrical gear stage

Splash losses according to MAUZ

The splash torque losses are calculated separately at the pinion and gear, with a correction factor to compensate for the reciprocal influence of the gears.

Equation 31.

T_{V Z 0, p l a n s c h} = 1.86 \cdot 10^{- 3} \cdot {(\frac{ν_{O i l}}{ν_{0}})}^{- 1.255} \cdot (\frac{r_{a}}{r_{0}}) \cdot C_{W Z} \cdot C_{W A} \cdot C_{M} \cdot C_{V} \cdot ν_{O i l} \cdot ρ_{O i l} \cdot A_{B} \cdot v_{t}

Symbol	Description	Unit
T_VZ0,plansch	Splash torque loss	Nm
ν_Oil	Kinematic viscosity at operating temperature (ν₀ = 1)	m²/s
r_a	Radius at tip circle (r₀ = 1)	m
C_WZ	Wall distance factor, oil feed side	-
C_WA	Wall distance factor, oil outflow side	-
C_M	Module factor	-
C_V	Oil volume factor	-
ρ_Oil	Oil density at operating temperature	kg/m³
A_B	Immersed wheel surface in operation	m²
v_t	Circumferential speed at pitch circle	m/s

Equation 32.

C_{W Z} = (0.08 \cdot \frac{s_{r Z}}{r_{a}} - 0.1) \cdot (\frac{v_{t}}{v_{t 0}}) - 0.08 \cdot \frac{s_{r Z}}{r_{a}} + 1.1

for s_rZ ≤ 1.3 and v_t ≥ 10 m/s

Equation 33.

C_{W Z} = 1.0

for s_rZ > 1.3 or v_t < 10 m/s

Symbol	Description	Unit
C_WZ	Wall distance factor, oil feed side	-
s_rZ	Distance between the tip circle diameter and casing on the immersed side of the gear	m
r_a	Radius at tip circle (r₀ = 1)	m
v_t	Circumferential speed at pitch circle (v_t0 = 10)	m/s

Equation 34.

C_{W A} = (0.06 - 0.05 \cdot \frac{s_{r A}}{r_{a}}) \cdot (\frac{v_{t}}{v_{t 0}}) + 0.05 \cdot \frac{s_{r A}}{r_{a}} + 0.95

for s_rA ≤ 1.3 and v_t ≥ 10 m/s

Equation 35.

C_{W A} = 1.0

for s_rA > 1.3 or v_t < 10 m/s

Symbol	Description	Unit
C_WA	Wall distance factor, oil outflow side	-
s_rA	Distance between the tip circle diameter and the casing on the emerged side of the gear	m
r_a	Radius at tip circle	m
v_t	Circumferential speed at pitch circle (v_t0 = 10)	m/s

Equation 36.

C_{M} = {(\frac{m_{n}}{m_{n 0}})}^{\frac{1}{7}}

Symbol	Description	Unit
C_M	Module factor	-
m_n	Normal module (m_n0 = 0.0045 · m_n)	m

Equation 37.

C_{V} = 1

for V_G/V_Oil ≥ 2.5

Equation 38.

C_{V} = 1 + \frac{1}{5} \cdot (\frac{V_{O i l} \cdot Q_{V 0}}{V_{G}} - 1) \cdot (\frac{v_{t}}{v_{t 0}} - 1)

where Q_V ₀ = 0.74 · e^-0.438

for V_G/V_Oil < 2.5

Symbol	Description	Unit
C_V	Oil volume factor	-
V_G	Volume of the casing	m³
V_Oil	Oil volume in the casing	m³
Q_V0	Factor for consideration of the immersion depth	-
e	Immersion depth	m
v_t	Circumferential speed at pitch circle (v_t0 = 10)	m/s

Equation 39.

A_{B} = r_{a}^{2} \cdot (α - sin α) + α \cdot r_{a} \cdot b

where

Equation 40.

α = 2 \cdot arccos (1 - \frac{e_{B}}{r_{a}})

Equation 41.

e_{B} = e - (0.4 \cdot v_{t}) \cdot 10^{- 3}

for v_t ≤ 30 m/s

Equation 42.

e_{B} = e - 0.012 \cdot m_{n}

for v_t > 30 m/s

Symbol	Description	Unit
A_B	Immersed wheel surface in operation	m²
r_a	Radius at tip circle	m
α	Opening angle of the immersed surface	deg
b	Face width	m
e_B	Operating immersion depth	m
e	Immersion depth	m
v_t	Circumferential speed at pitch circle	m/s
m_n	Normal module	m

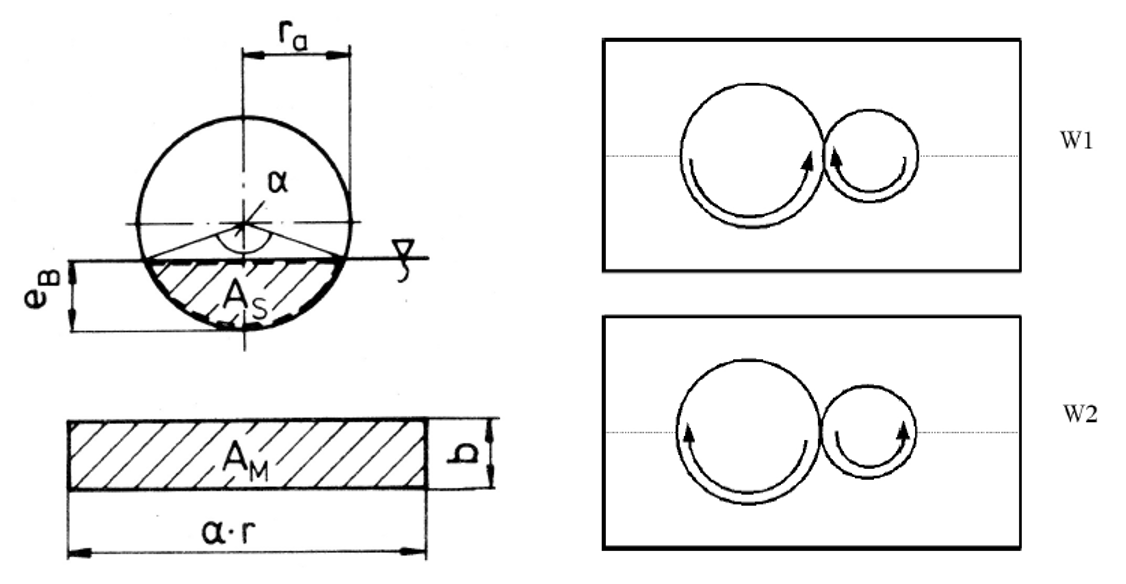Figure: Immersed wheel surface in operation and operating conditions

Equation 43.

K_{P 1 G} = {(\frac{v_{t}}{v_{t 0}})}^{\frac{1}{3} \cdot \sqrt{\frac{log ν_{O i l} + 6}{log (99 \cdot ν_{0})}} \cdot \sqrt[3]{\frac{b}{3 \cdot b_{0}}}}

for operating case W1, direct oil feed into the tooth mesh

Equation 44.

K_{P 1 G} = 1.0

for operating case W2, indirect oil feed into the tooth mesh via the wall of the casing

Symbol	Description	Unit
K_P1G	Correction factor for the simultaneously immersed mating gear	-
v_t	Circumferential speed at pitch circle (v_t0 = 10)	m/s
ν_Oil	Kinematic viscosity at operating temperature (ν₀ = 1)	m²/s
b	Face width (b₀ = 0.01)	m

This calculation method was derived from tests. The limit values of the tests also constitute the validity range of the method. However, these limits are conservative and results outside this range may also be valid.

Influencing variable	Symbol	Unit	from	to
Reynolds number	Re=(v_t·r_a)/ν	-	4125	531428
Relative immersion depth	e/r_a	-	0.04	1.0 (2.0)
Relative radial wall distance on the feed/outflow side	(s_rZ/rA)/r_a	-	0.03	3.15
Immersion depth relative to the height of the pitch point	e/h_c	-	0.02	1.0
Volume ratio	V_G/V_Oil	-	2.0	12.0
Gear ratio	u	-	1.0	2.0
Tip circle radius	r_a	mm	66	124
Face width	b	mm	10	60
Normal module	m_n	mm	3	6
Circumferential speed	v_t	m/s	10	60
Immersion depth	e	mm	5	135
Kinematic oil viscosity	ν	mm²/s	14	240
Density of the oil	ρ	kg/m³	855	881

Table: Validity range of the Mauz calculation equations

Load-independent gear losses with splash lubrication according to WALTER

The total hydraulic torque loss corresponds to the sum of the squeeze and splash torque losses, and is relative to the pinion or wheel shaft, depending on the load path.

Relative to the pinion shaft:

Equation 45.

T_{V Z 0, t a u c h} = T_{V Z 0, p l a n s c h, R i t z e l} + T_{V Z 0, p l a n s c h, R a d} \cdot \frac{1}{u} + T_{V Z 0, q u e t s c h}

Relative to the wheel shaft:

Equation 46.

T_{V Z 0, t a u c h} = T_{V Z 0, p l a n s c h, R i t z e l} \cdot u + T_{V Z 0, p l a n s c h, R a d} + T_{V Z 0, q u e t s c h}

Symbol	Description	Unit
T_VZ0,tauch	Load-independent gear torque loss with splash lubrication	Nm
T_VZ0,quetsch	Squeeze torque loss	Nm
T_{VZ0,plansch,Ritzel/Rad}	Splash loss of pinion/wheel	Nm
u	Gear ratio (z₂/z₁)	-

The power loss is calculated according to the reference shaft with the following formula:

Equation 47.

P_{V Z 0} = T_{V Z 0, t a u c h} \cdot 2 \cdot π \cdot n

Symbol	Description	Unit
P_VZ0,tauch	Load-independent gear losses with splash lubrication	W
T_VZ0,tauch	Load-independent gear torque losses with splash lubrication	Nm
n	Shaft speed	1/s

Squeeze losses according to WALTER

The squeeze torque loss of the gear mesh is calculated as follows:

Equation 48.

T_{V Z 0, q u e t s c h} = 3.88 \cdot 10^{- 10} \cdot C_{S p} \cdot ρ_{O i l} \cdot r_{w} \cdot b^{1.6} \cdot v_{t}^{2} \cdot ν_{O i l}^{- 0.15}

for direct oil feed into the gear mesh

Equation 49.

C_{S p} = {(\frac{e}{h_{c}})}^{1.5}

for indirect oil feed into the gear mesh via the wall of the casing

Equation 50.

C_{S p} = {(\frac{e}{h_{c}})}^{1.5} \cdot (\frac{2 \cdot h_{c}}{l_{h}})

Symbol	Description	Unit
T_VZ0,quetsch	Squeeze torque loss	Nm
C_Sp	Splash oil factor	-
ρ_Oil	Oil density at operating temperature	kg/m³
r_w	Radius at pitch circle of the deepest immersed gear	m
b	Minimum face width of pinion and wheel	m
v_t	Circumferential speed at pitch circle	m/s
ν_Oil	Kinematic viscosity at operating temperature (ν₀ = 1)	m²/s
e	Immersion depth of the deepest immersed gear	m
h_c	Height of the point of contact above the deepest immersed point of the cylindrical gear stage	m
l_h	Hydraulic length	m

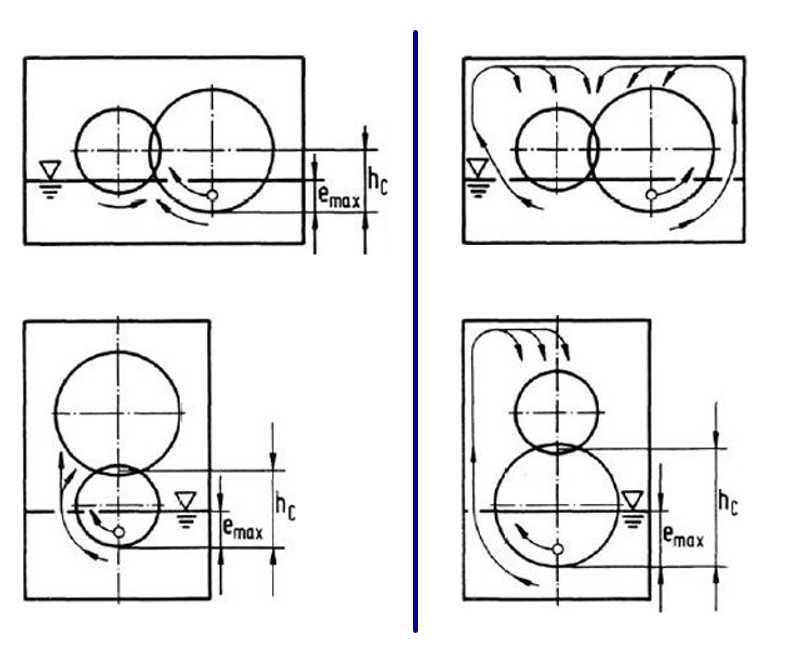Figure: Direct oil feed into the gear mesh (left), indirect via the wall of the casing (right)

Splash losses according to WALTER

The splash torque losses are calculated separately for the pinion and gear.

Equation 51.

T_{V Z 0, p l a n s c h} = C_{W} \cdot C_{V} \cdot C_{P L} \cdot ρ_{O i l} \cdot v_{t}^{2} \cdot r_{a}^{2} \cdot b

Symbol	Description	Unit
T_VZ0,plansch	Splash torque loss	Nm
C_W	Wall distance factor	-
C_V	Oil volume factor	-
C_PL	Splash torque factor	-
ρ_Oil	Oil density at operating temperature	kg/m³
v_t	Circumferential speed at pitch circle	m/s
r_a	Radius at tip circle	m
b	Face width	m

Equation 52.

C_{W} = 1

for s_rZ/(2 · r_a) ≥ 1

Equation 53.

C_{W} = 1 - 0.02 \cdot {(1 - \frac{s_{r Z}}{2 \cdot r_{a}})}^{1.8} \cdot {(\frac{v_{t}^{2}}{g \cdot r_{a}})}^{0.45}

for s_rZ/(2 · r_a) < 1

Symbol	Description	Unit
C_W	Wall distance factor	-
s_rZ	Distance between the tip circle diameter and casing at the immersing side of the gear	m
r_a	Radius at tip circle	m
v_t	Circumferential speed at pitch circle	m/s
g	Gravitational constant	m³/(kg · s²)

Equation 54.

C_{V} = 1

for V_Z/V_Oil ≤ 0.1

Equation 55.

C_{V} = 1 - {(\frac{V_{Z}}{V_{O i l}} - 0.1)}^{0.4}

for V_Z/V_Oil > 0.1

Symbol	Description	Unit
C_V	Oil volume factor	-
V_Z	Volume of oil displaced by the gear	m³
V_Oil	Oil volume in the casing	m³

Equation 56.

C_{P L} = 0.027 \cdot {(\frac{e}{r_{a}})}^{1.5} \cdot {(\frac{b}{r_{a}})}^{- 0.4} \cdot {(\frac{v_{t} \cdot r_{a}}{ν_{O i l}})}^{0.2} \cdot {(\frac{v_{t}^{2}}{g \cdot r_{a}})}^{- 0.5}

Symbol	Description	Unit
C_PL	Splash torque factor	-
e	Immersion depth	m
r_a	Radius at tip circle	m
b	Face width	m
v_t	Circumferential speed at pitch circle	m/s
ν_Oil	Kinematic viscosity at operating temperature	m²/s
g	Gravitational constant	m³/(kg · s²)

When C_V = 1 and C_W = 1, it results in the following simplified equation:

Equation 57.

T_{V Z 0, p l a n s c h} = 0.027 \cdot g^{0.5} \cdot ρ_{O i l} \cdot e^{1.5} \cdot b^{0.6} \cdot r_{a}^{1.6} \cdot v_{t}^{1.2} \cdot ν_{O i l}^{- 0.2}

Symbol	Description	Unit
T_VZ0,plansch	Splash torque loss	Nm
g	Gravitational constant	m³/(kg · s²)
ρ_Oil	Oil density at operating temperature	kg/m³
e	Immersion depth	m
b	Face width	m
r_a	Radius at tip circle	m
v_t	Circumferential speed at pitch circle	m/s
ν_Oil	Kinematic viscosity at operating temperature	m²/s

Influencing variable	Symbol	Unit	from	to
Reynolds number	Re=(v_t·r_a)/ν	-	7980	471429
Froude number	Fr=v_t²/(g · r_a)	-	93	4645
Relative immersion depth	e/r_a	-	0.12	1.71
Relative width	b/r_a	-	0.09	0.63
Relative tooth depth	h/m_n	-	2.25	-
Relative radial wall distance on the feed side	s_rZ/(2r_a)	-	0.16	1.56
Relative oil volume	V_Z/V_Oil	-	0.01	0.20
Hydraulic length	l_H=(4A_G)/U	mm	629	1332
Tip circle radius	r_a	mm	79	110
Face width	b	mm	5	10
Normal module	m_n	mm	3	6
Circumferential speed	v_t	m/s	10	60
Kinematic oil viscosity	ν	mm²/s	14	99
Density of the oil	ρ	kg/m³	850	-

Table: Validity range for the Walter calculation equations

Injection lubrication

For injection lubrication, the calculation method is automatically determined by the existing circumferential speed v_t. Thus, for v_t > 60 m/s, the squeeze and pulse losses are calculated according to BUTSCH; for v_t < 60 m/s, the squeeze losses are calculated according to MAUZ and the pulse losses are calculated according to ARIURA. Detailed warnings are issued if the validity range of the BUTSCH squeeze loss calculation equations is left; however, the calculation continues if possible.

Equation 58.

P_{V Z 0, e i n s p r i t z} = P_{V Z 0, i m p u l s} + P_{V Z 0, q u e t s c h} + P_{V Z 0, v e n t i l a t i o n}

Symbol	Description	Unit
P_{VZ0,einspritz}	Load-independent gear losses with injection lubrication	W
P_VZ0,impuls	Pulse losses: flow deflection of an oil stream impacting the tooth flanks	W
P_VZ0,quetsch	Squeeze losses: squeezing out of excess oil in the tooth contact	W
P_{VZ0,ventilation}	Ventilation losses: turbulence of the injected oil	W

Splash losses do not occur with injection lubrication, or are negligible and therefore not calculated.

Ventilation losses are calculated according to MAURER, as long as the calculation is not disabled.

Squeeze losses according to MAUZ for v_t < 60 m/s

For squeezing losses, a differentiation is made between injection at the beginning and end of the engagement.

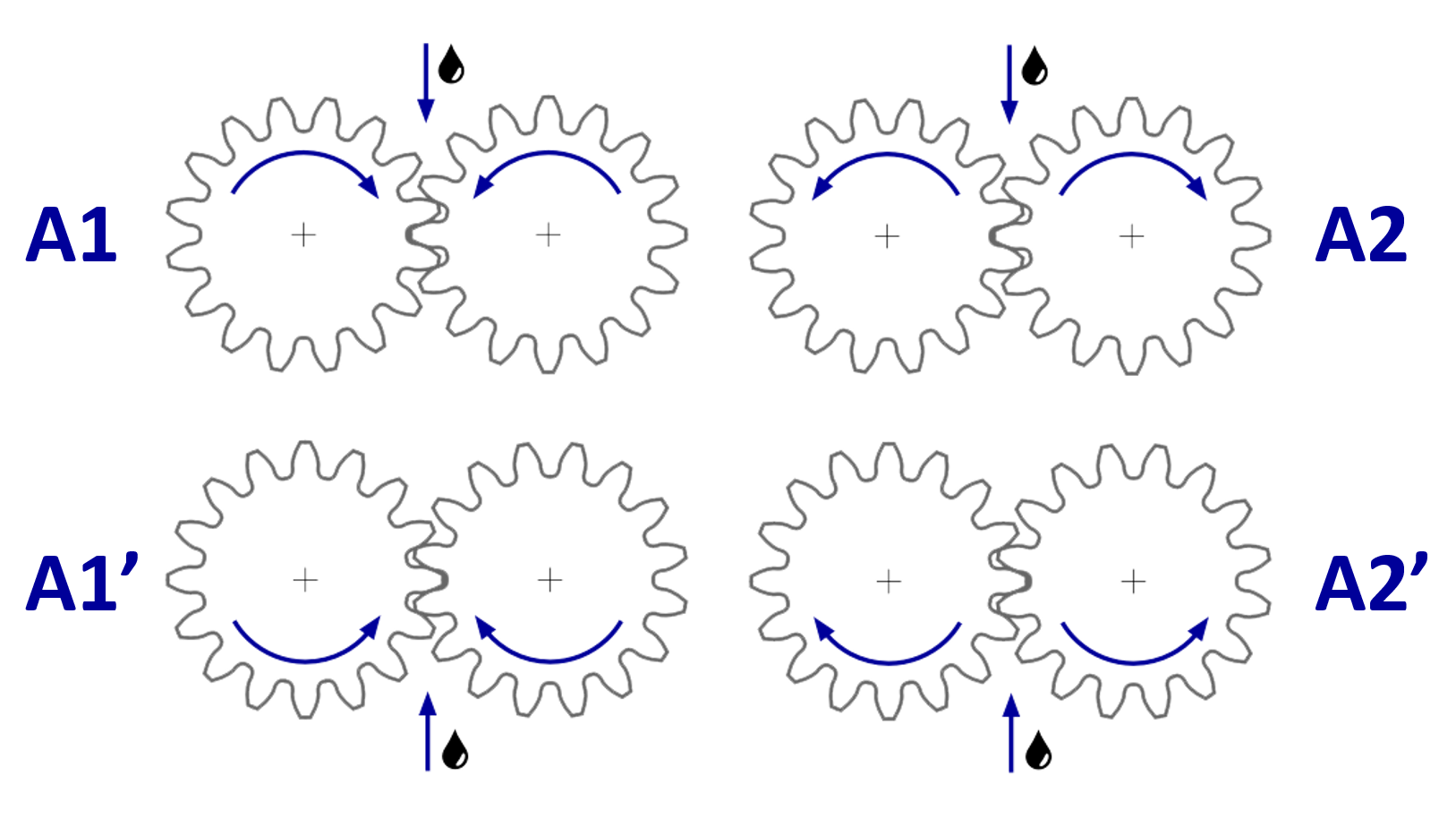Figure: Injection variants

Injection at the beginning of the mesh (A1 and A1’) :

Equation 59.

T_{V Q} = C_{1} \cdot 4.12 \cdot ρ_{O i l} \cdot Q_{e}^{0.75} \cdot r_{w} \cdot v_{t}^{1.25} \cdot b^{0.25} \cdot m_{n}^{0.25} \cdot {(\frac{ν_{O i l}}{ν_{0}})}^{0.25} \cdot {(\frac{h_{Z}}{h_{Z 0}})}^{0.5}

where C1 = 1 for injection variant A1

where C1 = 0.9 for injection variant A1‘

Injection at the end of the mesh (A2 and A2’) :

Equation 60.

T_{V Q} = C_{2} \cdot ρ_{O i l} \cdot Q_{e} \cdot r_{w} \cdot (v_{t} + v_{s})

where C2 = 1 for injection variant A2

where C2 = 0.85 for injection variant A2‘

Symbol	Description	Unit
T_VQ	Squeeze torque loss	Nm
C_1/2	Constants, depending on the injection variant	-
ρ_Oil	Oil density at operating temperature	kg/m³
Q_e	Injected oil volume flow rate	m³/s
r_w	Radius at pitch circle	m
v_t	Circumferential speed at pitch circle	m/s
v_s	Injection speed	m/s
b	Face width	m
m_n	Normal module	m
ν_Oil	Kinematic viscosity at operating temperature (ν₀ = 1)	m²/s
h_Z	Working depth (h_Z0 = 2.3 ·m_n)	m

Squeeze losses according to BUTSCH for v_t > 60 m/s

MAUZ differentiates between injection at the beginning and end of the mesh. The following relative values are introduced for both cases:

Equation 61.

v_{t}^{*=} \frac{v_{t}}{100 [m / s]}

Equation 62.

Q_{e}^{*=} Q_{e} \cdot \frac{6 \cdot 10^{2}}{1 [m^{3} / s]}

Equation 63.

b^{*=} \frac{b}{0.1 [m]}

Equation 64.

r^{*=} \frac{2 \cdot u}{u + 1}

Injection into the beginning of the mesh (A1) :

Equation 65.

T_{V Q} = C_{1} \cdot v_{t}^{*} + C_{2}

where

Equation 66.

C_{1} = 18 \cdot {(\frac{Q_{e}^{*}}{b^{*}})}^{\frac{0.8}{b^{*}}} \cdot {(b^{*})}^{1.8} \cdot {(r^{*})}^{1.1} - 12.75 \cdot Q_{e}^{*} \cdot r^{*}

Equation 67.

C_{2} = 8 \cdot {(\frac{Q_{e}^{*}}{b^{*}})}^{0.5} \cdot {(b^{*})}^{- 0.3} \cdot {(r^{*})}^{1.1} + 2.35 \cdot Q_{e}^{*} \cdot r^{*}

Injection into the end of the mesh (A2) :

Equation 68.

T_{V Q} = C_{3} + C_{4} \cdot (v_{t}^{*} - 0.6) + C_{5} \cdot ({(v_{t}^{*})}^{2} - {0.6}^{2})

where

Equation 69.

C_{3} = 0.5 - {(r^{*})}^{- 2}

Equation 70.

C_{4} = 17.2 \cdot {(r^{*})}^{1.5} - 12.75 \cdot (\frac{Q_{e}^{*}}{b^{*}}) \cdot r^{*}

Equation 71.

C_{5} = - 6.3 \cdot \frac{{(r^{*})}^{1.5}}{1 + (\frac{Q_{e}^{*}}{b^{*}})}

Symbol	Description	Unit
T_VQ	Squeeze torque loss	Nm
C_3/4/5	Constants, depending on the injection variant	-
v_t*	Relative dimensionless circumferential speed at pitch circle	-
v_t	Circumferential speed at pitch circle	m/s
Q_e*	Relative dimensionless injected oil volume flow	-
Q_e	Injected oil volume flow	m³/s
b*	Relative dimensionless face width	-
b	Face width	m
r*	Relative dimensionless radius	-
u	Gear ratio (z₂/z₁)	-

The validity range for both injection variants is:

ISO VG oil viscosity 22 to 86
Face width 0.075 m ≤ b ≤ 0.125 m
Circumferential speed 60 m/s ≤ v_t ≤ 200 m/s
Solid steam nozzles

Pulse losses according to AIURA for v_t < 60 m/s

Injection at the beginning of the mesh (A1 and A1‘):

Equation 72.

T_{V I} = r_{w} \cdot ρ_{O i l} \cdot Q_{e} \cdot (v_{t} - v_{s}) \cdot C_{1}

Injection at the end of the mesh (A2 and A2‘):

Equation 73.

T_{V I} = r_{w} \cdot ρ_{O i l} \cdot Q_{e} \cdot (v_{t} + v_{s}) \cdot C_{1}

where C1 = 1 for injection variant A1

where C1 = 0.9 for injection variant A1‘

where C1 = 1 for injection variant A2

where C1 = 0.85 for injection variant A2‘

Symbol	Description	Unit
T_VI	Pulse torque loss	Nm
C₁	Constant, depending on the injection variant	-
r_w	Radius at pitch point	m
ρ_Oil	Oil density at operating temperature	kg/m³
Q_e	Injected oil volume flow	m³/s
v_t	Circumferential speed at pitch circle	m/s
v_s	Injection speed	m/s

If the injection speed drives the gears, this results in negative losses. In this case, the pulse losses are set to 0.

Pulse losses according to BUTSCH for v_t > 60 m/s

Injection into the beginning of the mesh (A1 and A1‘):

Equation 74.

T_{V I} = r_{w 2} \cdot ρ_{O i l} \cdot Q_{e} \cdot (v_{t} - v_{s})

Injection into the end of the mesh (A2 and A2‘):

Equation 75.

T_{V I} = r_{w 2} \cdot ρ_{O i l} \cdot Q_{e} \cdot (v_{t} + v_{s})

Symbol	Description	Unit
T_VI	Pulse torque loss	Nm
r_w2	Radius of the wheel at pitch circle	m
ρ_Oil	Oil density at operating temperature	kg/m³
Q_e	Injected oil volume flow	m³/s
v_t	Circumferential speed at pitch circle	m/s
v_s	Injection speed	m/s

If the injection speed drives the gears, this results in negative losses. In this case, the pulse losses are set to 0.

Ventilation losses according to MAURER

The amount of ventilation losses for the pinion and the wheel are calculated as:

Equation 76.

T_{V V, R i t z e l} = 1.37 \cdot 10^{- 9} \cdot v_{t}^{1.90} \cdot d_{w 1}^{1.60} \cdot b_{1}^{0.52} \cdot m_{t}^{0.69}

Equation 77.

T_{V V, R a d} = 1.37 \cdot 10^{- 9} \cdot v_{t}^{1.90} \cdot d_{w 2}^{1.60} \cdot b_{2}^{0.52} \cdot m_{t}^{0.69}

The amount of torque caused by the mating gear is calculated as:

Equation 78.

T_{V V, E i n g r i f f} = 1.17 \cdot 10^{- 6} \cdot v_{t}^{1.95} \cdot u^{0.73} \cdot b^{1.37}

The ventilation torque loss of the gear pair is relative to the gear shaft. Therefore, the ventilation torque loss of the pinion is multiplied by the gear ratio to determine the losses of the gear pair. The ventilation torque loss of the gear pair is then calculated as follows:

Equation 79.

T_{V V, R a d p a a r} = (T_{V V, R a d} + u \cdot T_{V V, R i t z e l} + T_{V V, E i n g r i f f}) \cdot F_{W a n d} \cdot F_{O i l}

where

Equation 80.

F_{W a n d} = 0.763 \cdot s_{u}^{0.26} \cdot s_{v w}^{- 0.0043 \cdot (2.11 \cdot s_{u} - 9.53)}

Equation 81.

F_{O i l} = 0.934 \cdot Q_{e}^{0.163}

Symbol	Description	Unit
T_{VV,Ritzel/Rad}	Ventilation torque loss of pinion/gear	Nm
v_t	Circumferential speed at pitch circle	m/s
d_w1/2	Pitch diameter of pinion/gear	mm
b_1/2	Face width of pinion/gear	mm
T_VV,Eingriff	Ventilation torque loss from the mating gear	Nm
u	Gear ratio (z₂/z₁)	-
b	Minimum face width of pinion and gear	mm
T_VV,Radpaar	Ventilation torque loss of the gear pair	Nm
F_Wand	Factor for wall effects	-
F_Oil	Factor for oil effects	-
s_u	Minimum frontal distance to casing wall	mm
s_vw	Minimum radial distance to casing wall	mm
Q_e	Injected oil volume flow	l/min

Load-independent gear losses for worm stages

A model from FVA 729 I for calculation of the splash power loss of cylindrical gear stages is applied to worm gear stages:

Equation 82.

P_{V Z 0} = (\frac{1}{2} \cdot ρ_{O i l} \cdot {(\frac{π \cdot n}{30})}^{2} \cdot A \cdot {(\frac{d_{m}}{2})}^{3} \cdot C_{m}) \cdot ω

where

Equation 83.

C_{m} = {(\frac{2 \cdot e}{d_{m}})}^{0.45} \cdot {(\frac{V_{0}}{d_{m}})}^{0.1} \cdot F r^{- 0.6} \cdot R e^{- 0.21}

Equation 84.

F r = \frac{ω^{2} \cdot d_{m}}{2 \cdot g}

Equation 85.

R e = \frac{ω^{2} \cdot d_{m}^{2}}{4 \cdot ν_{O i l}}

Symbol	Description	Unit
P_VZ0	Load-independent gear losses	W
ρ_Oil	Oil density at operating temperature	kg/m³
n	Speed	1/min
A	Oil-covered surface	mm²
d_m	Reference circle/pitch diameter	m
ω	Rotational speed	1/s
C_m	Splash factor	-
e	Immersion depth	m
V₀	Oil volume	m³
Fr	Froude number	-
g	Gravitational constant	m³/(kg · s²)
Re	Reynolds number	-
ν_Oil	Kinematic viscosity at operating temperature	m²/s

Only the splash losses of the worm gear are calculated. The worm itself is not considered, as with shafts.

Rolling bearing losses

The power loss from rolling bearings is determined using the current catalog methods of the manufacturers SKF, SCHAEFFLER and TIMKEN. If this is not possible or not desired, the power loss can be calculated according to ISO 14179-2. This corresponds to the SKF catalog method from 1994.

Figure: Current SKF, SCHAEFFLER, and TIMKEN bearing catalogs from 2020

The following only provides a rough overview of the calculation methods. For more detailed information, refer to the manufacturers' bearing catalogs, which are available free of charge.

SKF 2020

The SKF catalog method is the most precise and detailed calculation approach for determining the power loss. The individual friction torque amounts are summed to determine the total torque loss. This can also be used to identify which amount of torque loss is the greatest and where improvements may be achieved.

Equation 86.

M = M_{r r} + M_{s l} + M_{s e a l} + M_{d r a g}

Symbol	Description	Unit
M	Total friction torque	Nm
M_rr	Rolling friction torque	Nm
M_sl	Sliding friction torque	Nm
M_seal	Friction torque of contact seals	Nm
M_drag	Friction torque due to flow, splash, or spray losses	Nm

Equation 87.

M_{r r} = ϕ_{i s h} \cdot ϕ_{r s} \cdot G_{r r} \cdot (ν_{O i l} \cdot n)^{0.6}

Symbol	Description	Unit
M_rr	Rolling friction torque	Nm
ϕ_ish	Lubricating film thickness factor for rolling friction torque	-
ϕ_rs	Kinematic lubricant displacement factor for rolling friction torque	-
G_rr	Basic rolling friction value, depending on the bearing geometry and input load	-
ν_Oil	Kinematic operating oil viscosity	mm²/s
n	Relative speed between bearing inner and outer ring	1/min

Equation 88.

M_{s l} = G_{s l} \cdot μ_{s l}

Symbol	Description	Unit
M_sl	Sliding friction torque	Nm
G_sl	Basic sliding friction value, depending on the bearing geometry and input load	-
µ_sl	Coefficient of sliding friction	-

Equation 89.

M_{s e a l} = K_{S 1} \cdot d_{S}^{β} + K_{S 2}

Symbol	Description	Unit
M_seal	Friction torque of the contact seals	Nm
K_S1	Coefficient of sealing friction 1, depending on the seal and bearing types and the bearing dimensions	-
d_S	Diameter of the mating surface of the seal	mm
β	Sealing friction exponent, depending on the seal and bearing type	-
K_S2	Coefficient of sealing friction 2, depending on the seal and bearing types and the bearing dimensions	-

Ball bearings

Equation 90.

M_{d r a g} = 0.4 \cdot V_{M} \cdot K_{b a l l} \cdot d_{m}^{5} \cdot n^{2} + 1.093 \cdot 10^{- 7} \cdot n^{2} \cdot d_{m}^{3} \cdot {(\frac{n \cdot d_{m}^{2} \cdot f_{t}}{ν_{O i l}})}^{- 1.379} \cdot R_{S}

Cylindrical roller bearings

Equation 91.

M_{d r a g} = 4 \cdot V_{M} \cdot K_{r o l l} \cdot d_{m}^{4} \cdot n^{2} + 1.093 \cdot 10^{- 7} \cdot n^{2} \cdot d_{m}^{3} \cdot {(\frac{n \cdot d_{m}^{2} \cdot f_{t}}{ν_{O i l}})}^{- 1.379} \cdot R_{S}

Symbol	Description	Unit
M_drag	Friction torque due to flow, splash, or spray losses for oil bath lubrication	Nm
V_M	Flow loss factor	-
K_ball, K_roll	Rolling element-related constants, depending on the bearing type and dimensions as well as the number of rolling elements	-
d_m	Average bearing diameter 0.5·(d+D)	mm
n	Relative speed between bearing inner and outer ring	1/min
f_t	Factor for immersion depth in oil bath, depending on the bearing dimensions and oil level	-
ν_Oil	Kinematic operating oil viscosity	mm²/s
R_S	Oil bath factor, depending on the bearing type and dimensions as well as the oil level	-

Additional information on the calculation can be found in the SKF Bearing Catalog.

There is also an SKF Online Tool for bearing calculations, which includes the power loss.

SCHAEFFLER 2020

The SCHAEFFLER catalog method is based on simple empirically determined characteristics for calculation of the total friction torque as a function of the load-dependent and load-independent loss amounts. Axial loads are considered separately.

Equation 92.

M_{R} = M_{0} + M_{1} + M_{2}

Symbol	Description	Unit
M_R	Total friction torque	Nm
M₀	Load-independent bearing friction torque	Nm
M₁	Load-dependent bearing friction torque	Nm
M₂	Bearing friction torque for axially loaded cylindrical roller bearings	Nm

Speed-dependent friction torque

Equation 93.

M_{0} = 10^{- 7} \cdot f_{0} \cdot (ν_{O i l} \cdot n)^{\frac{2}{3}} \cdot d_{m}^{3}

for

Equation 94.

ν_{O i l} \cdot n \geq 2000 \frac{m m^{2}}{s \cdot min}

Equation 95.

M_{0} = 160 \cdot 10^{- 7} \cdot f_{0} \cdot d_{m}^{3}

for

Equation 96.

ν_{O i l} \cdot n < 2000 \frac{m m^{2}}{s \cdot min}

Symbol	Description	Unit
M₀	Load-independent bearing friction torque	Nm
f₀	Load-dependent bearing friction torque	-
ν_Oil	Kinematic operating oil viscosity	mm²/s
n	Relative speed between bearing inner and outer ring	1/min
d_m	Average bearing diameter 0.5·(d+D)	mm

Load-dependent friction torque

for needle and cylindrical roller bearings

Equation 97.

M_{1} = f_{1} \cdot F \cdot d_{m}

for ball, bevel, and spherical roller bearings

Equation 98.

M_{1} = f_{1} \cdot P_{1} \cdot d_{m}

Symbol	Description	Unit
M₁	Load-dependent bearing friction torque	Nm
f₁	Load-dependent bearing friction factor	-
F	Radial load for radial bearings and axial load for axial bearings	N
d_m	Average bearing diameter 0.5·(d+D)	mm
P₁	Relevant load for friction torque	N

Equation 99.

M_{2} = f_{2} \cdot F_{a} \cdot d_{m}

Symbol	Description	Unit
M₂	Bearing friction torque for axially loaded cylindrical roller bearings	Nm
f₂	Bearing friction factor, depending on the axial load	-
F_a	Axial dynamic bearing load	N
d_m	Average bearing diameter 0.5·(d+D)	mm

Additional information on the calculation can be found in the SCHAEFFLER Bearing Catalog.

There is also a SCHAEFFLER Online Tool for bearing calculations, which includes the power loss.

TIMKEN 2020

The TIMKEN catalog method is based on simple empirically determined characteristic values for calculation of the total friction torque as a function of the load-independent and load-dependent losses. The formula is very similar to the SCHAEFFLER calculation.

Equation 100.

M = f_{1} \cdot F_{β} \cdot d_{m} + 10^{- 7} \cdot f_{0} \cdot (ν_{O i l} \cdot n)^{\frac{2}{3}} \cdot d_{m}^{3}

for

Equation 101.

ν_{O i l} \cdot n \geq 2000 \frac{m m^{2}}{s \cdot min}

Equation 102.

M = f_{1} \cdot F_{β} \cdot d_{m} + 160 \cdot 10^{- 7} \cdot f_{0} \cdot d_{m}^{3}

for

Equation 103.

ν_{O i l} \cdot n < 2000 \frac{m m^{2}}{s \cdot min}

with

Radial ball bearings:

Equation 104.

F_{β} = max (0.9 \cdot F_{a} \cdot cot α - 0.1 \cdot F_{r}; F_{r})

Radial cylindrical and spherical roller bearings:

Equation 105.

F_{β} = max (0.8 \cdot F_{a} \cdot cot α; F_{r})

Thrust, cylindrical roller, and spherical roller thrust bearings:

Equation 106.

F_{β} = F_{a}

Symbol	Description	Unit
M	Total friction torque	Nm
f₁	Load-dependent bearing friction factor	-
F_β	Bearing load for the load-dependent bearing friction torque	N
F_a, F_r	Axial or radial bearing load	N
α	Nominal contact angle	deg
f₀	Load-independent bearing friction factor	-
d_m	Average bearing diameter 0.5·(d+D)	mm
ν_Oil	Kinematic operating oil viscosity	mm²/s
n	Relative speed between bearing inner and outer ring	1/min

Tapered roller bearings

Single-row:

Equation 107.

M = k_{1} \cdot G_{1} \cdot (n \cdot ν_{O i l})^{0.62} \cdot {(\frac{f_{3} \cdot F_{r}}{K})}^{0.3}

Double-row:

Equation 108.

M = k_{1} \cdot G_{1} \cdot (n \cdot ν_{O i l})^{0.62} \cdot {(\frac{0.06}{K})}^{0.3} \cdot (F_{r A}^{0.3} + F_{r B}^{0.3})

Symbol	Description	Unit
M	Total friction torque	Nm
k₁	Bearing torque constant	-
G₁	Geometry factor	-
ν_Oil	Kinematic operating oil viscosity	mm²/s
n	Relative speed between bearing inner and outer ring	1/min
f₃	Combined load factor	-
F_r	Radial load	N
K	K factor	-
F_rA, F_rB	Radial load of row A or B	N

Additional details on the calculation are available in the TIMKEN bearing catalog.

ISO 14179-2

The calculation of bearing losses according to ISO 14179-2 corresponds to the SKF bearing catalog method from 1994.

Equation 109.

M = M_{0} + M_{1} + M_{2}

Symbol	Description	Unit
M	Total friction torque	Nm
M₀	Load-independent bearing friction torque	Nm
M₁	Load-dependent bearing friction torque	Nm
M₂	Bearing friction torque for axially loaded cylindrical roller bearings	Nm

Speed-dependent friction torque

Equation 110.

M_{0} = 10^{- 10} \cdot f_{0} \cdot {(ν_{O i l} \cdot n)}^{\frac{2}{3}} \cdot d_{m}^{3}

for

Equation 111.

ν_{O i l} \cdot n \geq 2000 \frac{m m^{2}}{s \cdot min}

Equation 112.

M_{0} = 1.6 \cdot 10^{- 8} \cdot f_{0} \cdot d_{m}^{3}

for

Equation 113.

ν_{O i l} \cdot n < 2000 \frac{m m^{2}}{s \cdot min}

Symbol	Description	Unit
M₀	Load-independent bearing friction torque	Nm
f₀	Load-independent bearing friction factor, depending on the bearing and lubrication types	-
d_m	Average bearing diameter 0.5·(d+D)	mm
ν_Oil	Kinematic operating oil viscosity	mm²/s
n	Relative speed between bearing inner and outer ring	1/min

Load-dependent friction torque

Equation 114.

M_{1} = f_{1} \cdot P_{1}^{a} \cdot d_{m}^{b} \cdot 10^{- 3}

Symbol	Description	Unit
M₁	Load-dependent bearing friction torque	Nm
f₁	Load-dependent bearing friction factor	-
P₁	Equivalent bearing load for friction torque	N
a, b	Exponents	-
d_m	Average bearing diameter 0.5·(d+D)	mm

Equation 115.

M_{2} = f_{2} \cdot F_{a} \cdot d_{m} \cdot 10^{- 3}

Symbol	Description	Unit
M₂	Bearing friction torque for axially-loaded cylindrical roller bearings	Nm
f₂	Bearing friction factor, depending on the axial load	-
F_a	Axial dynamic bearing load	N
d_m	Average bearing diameter 0.5·(d+D)	mm

When this calculation method is selected, factors f₀ and f₁ must be specified manually. The relevant tables from ISO 14179-2 can be found in the Attribute Help.

Plain bearing losses

Power loss from plain bearings is calculated in the COMBROS R & A modules, which have long been integrated into the FVA-Workbench for iterative solution of the overall system. The friction torques calculated in COMBROS are considered in the determination of losses in the overall system.

Combros R&A

The COMBROS R (radial) and A (axial) calculation modules were developed at the TU Clausthal ITR (Institut für Tribologie und Energiewandlungsmaschinen) as part of FVA Projects FVA 577, FVA 668II, and FVA 677.

Planet carrier losses

Planet carrier power losses with single-plate carriers are a result of the carrier and planets splashing in oil. For dual-plate carriers, the planets do not have any additional influence on the splash losses, as they are located within the planet carrier.

The losses from the rotation of the planets are considered separately and added to those of the planet itself.

The methodology for calculation of planet carrier losses was developed by KETTLER.

Single-plate planet carriers according to KETTLER

For open single-plate planet carriers, the splash losses of the carrier and the planets rotating within it are added together.

Equation 116.

P_{V S T} = P_{V S T, s w 1} + P_{V S T, s r 1}

Symbol	Description	Unit
P_VST	Single-plate planet carrier splash power loss	W
P_VST,sw1	Single-plate planet carrier side plate splash power loss	W
P_VST,sr1	Single-plate planet carrier planet gear splash power loss due to rotation of the carrier	W

Equation 117.

P_{V S T, s w 1} = 4.6295 \cdot 10^{- 3} \cdot d_{S t 1}^{3.8} \cdot b_{S t 1} \cdot F_{e, S t 1}^{1.1945} \cdot n_{s 0}^{1.8559} \cdot ν_{O i l}^{0.22} \cdot ρ_{O i l}

Symbol	Description	Unit
P_VST,sw1	Single-plate planet carrier side plate splash power loss	W
d_St1	Total diameter of the single-plate planet carrier	m
b_St1	Rim width of the single-plate planet carrier	m
F_e,St1	Planet carrier side plate oil level influence factor	-
n_s0	Planet carrier speed	min^-1
ν_Oil	Kinematic operating oil viscosity	mm²/s
ρ_Oil	Oil density at operating temperature	kg/m³

where

Equation 118.

F_{e, S t 1} = 1

Equation 119.

s_{O i l} > \frac{1}{2} \cdot d_{S t 1}

Equation 120.

F_{e, S t 1} = \frac{1}{π} \cdot arccos (\frac{- 2 \cdot s_{O i l}}{d_{S t 1}})

Equation 121.

s_{O i l} \leq \frac{1}{2} \cdot d_{S t 1}

and

Equation 122.

s_{O i l} \geq - \frac{1}{2} \cdot d_{S t 1}

Equation 123.

F_{e, S t 1} = 0

Equation 124.

s_{O i l} < - \frac{1}{2} \cdot d_{S t 1}

Symbol	Description	Unit
F_e,St1	Single-plate planet carrier side plate oil level influence factor	-
s_Oil	Oil level relative to the center of the gear	m
d_St1	Total diameter of the single-plate planet carrier	m

Equation 125.

P_{V S T, s r 1} = 1.2096 \cdot 10^{- 2} \cdot F a k_{P l 1} \cdot | a |^{2.6} \cdot d_{a, P l} \cdot b_{P l} \cdot F_{e, a S t 1}^{0.9013} \cdot n_{s 0}^{2.3706} \cdot ρ_{O i l}

Symbol	Description	Unit
P_VST,sr1	Single-plate planet carrier planet gear splash power loss due to rotation of the carrier	W
Fak_Pl1	Single-plate planet carrier number of planetary gears influence factor	-
a	Center distance	m
d_a,Pl	Planetary gear tip diameter	m
b_Pl	Planetary gear width	m
F_e,aSt1	Single-plate planet carrier planetary gear oil level influence factor	-
n_s0	Planet carrier speed	min^-1
ρ_Oil	Oil density at operating temperature	kg/m³

where

Equation 126.

F a k_{P l 1} = 1.1724

Equation 127.

z_{P l} = 3

Equation 128.

F a k_{P l 1} = 1.1829

Equation 129.

z_{P l} > 3

and

Equation 130.

F_{e, a S t 1} = 1

Equation 131.

s_{O i l} > a

Equation 132.

F_{e, a S t 1} = \frac{1}{π} \cdot arccos (\frac{- s_{O i l}}{a})

Equation 133.

s_{O i l} > - a

Equation 134.

F_{e, a S t 1} = 0

Equation 135.

s_{O i l} < - a

Symbol	Description	Unit
Fak_Pl1	Single-plate planet carrier number of planetary gears influence factor	-
z_Pl	Number of planets	-
F_e,aSt1	Single-plate planet carrier planetary gear oil level influence factor	-
s_Oil	Oil level relative to the center of the gear	m
a	Center distance in the coordinate system	m

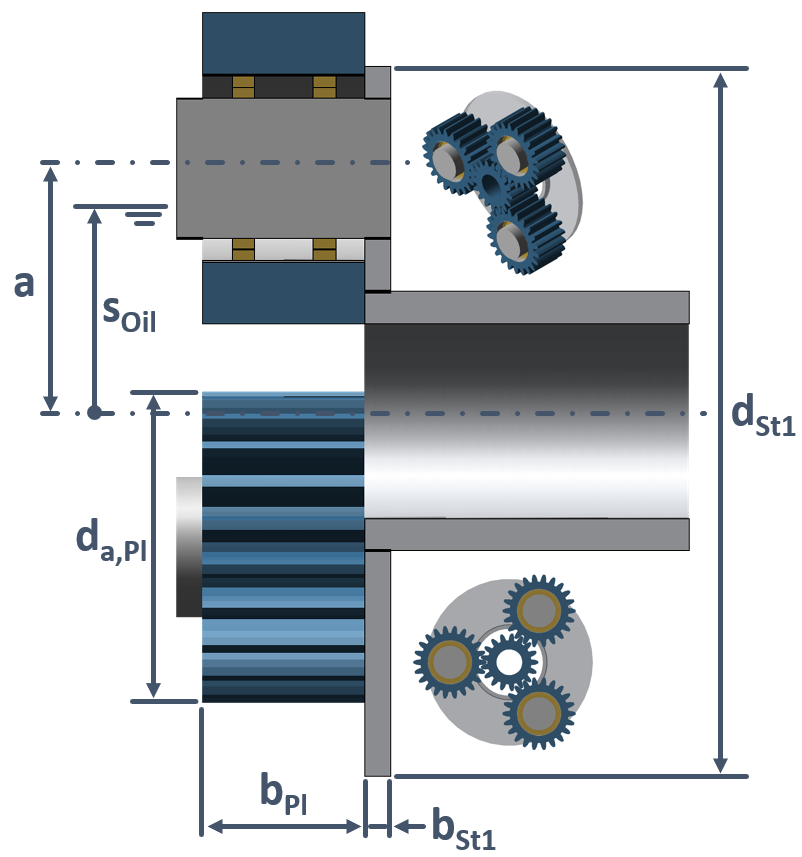Figure: Single-plate planet carrier geometric data

Dual-plate planet carriers according to KETTLER

For open dual-plate planet carriers, the splash losses are caused exclusively by the carrier splashing in oil.

Equation 136.

P_{V S T, s w 2} = 4.6295 \cdot 10^{- 3} \cdot d_{S t 2}^{3.8} \cdot b_{S t 2} \cdot F_{e, S t 2}^{1.1945} \cdot n_{s 0}^{1.8559} \cdot ν_{O i l}^{0.22} \cdot ρ_{O i l}

Symbol	Description	Unit
P_VST,sw2	Dual-plate planet carrier side plate splash power loss	W
d_St2	Total diameter of the dual-plate planet carrier	m
b_St2	Dual-plate planet carrier rim width	m
F_e,St2	Dual-plate planet carrier planetary gear oil level influence factor	-
n_s0	Planet carrier speed	min^-1
ν_Oil	Kinematic operating oil viscosity	mm²/s
ρ_Oil	Oil density at operating temperature	kg/m³

where

Equation 137.

F_{e, S t 2} = 1

Equation 138.

s_{O i l} > \frac{1}{2} \cdot d_{S t 2}

Equation 139.

F_{e, S t 2} = \frac{1}{π} \cdot arccos (\frac{- 2 \cdot s_{O i l}}{d_{S t 2}})

Equation 140.

s_{O i l} \leq \frac{1}{2} \cdot d_{S t 2}

and

Equation 141.

s_{O i l} \geq - \frac{1}{2} \cdot d_{S t 2}

Equation 142.

F_{e, S t 2} = 0

Equation 143.

s_{O i l} < - \frac{1}{2} \cdot d_{S t 2}

Symbol	Description	Unit
F_e,St2	Dual-plate planet carrier planetary gear oil level influence factor	-
s_Oil	Oil level relative to the center of the gear	m
d_St2	Total diameter of the dual-plate planet carrier	m

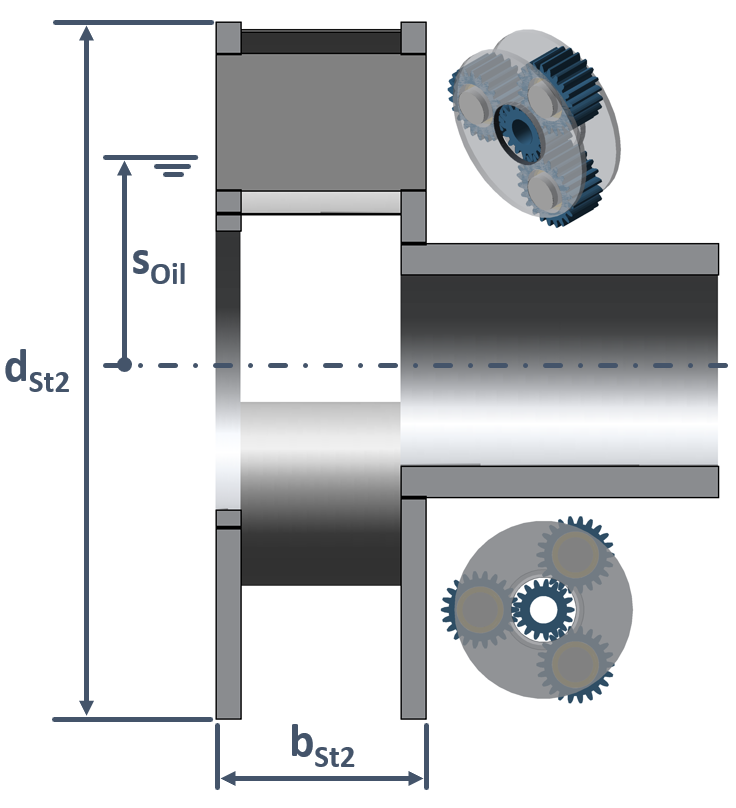Figure: Dual-plate planet carrier geometric data

Sealing losses

Power loss from radial shaft seals are a result of friction between the seal, which is generally fixed, and the rotating shaft. These friction losses depend on various factors, such as the seal material, hardness of the shaft material, surface roughness of the shaft in the area of the seal lip, the lubricant, and the temperature at the location of the seal. The calculation is performed using simplified empirically determined formulas and factors.

ISO 14179-1 (USA)

ISO/TR 14179-1 is the American ISO approach for gearbox thermal balance calculations. It includes calculation of the sealing losses based on the rules and regulations of the Association for Rubber Products Manufacturers (ARPM OS-15).

Equation 144.

P_{V D} = \frac{T_{S} \cdot n}{9549}

where

Equation 145.

T_{S} = 3.737 \cdot d_{s h}

for VITON

Equation 146.

T_{S} = 2.429 \cdot d_{s h}

for BUNA N

Symbol	Description	Unit
P_VD	Power loss at the seal	W
d_sh	Shaft diameter at the seal	mm
n	Speed of the shaft relative to the seal	1/min

ISO 14179-2 (Germany)

ISO/TR 14179-2 is the German ISO approach for gearbox thermal balance calculations. It includes calculation of the sealing losses based on the Simrit/Freudenberg (SIMRIT) catalog for radial shaft seals.

Equation 147.

P_{V D} = 7.69 \cdot 10^{- 6} \cdot d_{s h}^{2} \cdot n

Symbol	Description	Unit
P_VD	Power loss at the seal	W
d_sh	Shaft diameter at the seal	mm
n	Speed of the shaft relative to the seal	1/min

LINKE

Heinz Linke describes an extension of the ISO 14179-2 approach for calculating sealing losses in his book on cylindrical gears (LINKE). This approach extends the calculation to include the influence of the lubricant at different operating temperatures.

Equation 148.

P_{V D} = [145 - 1.6 \cdot ϑ_{O i l} + 350 lg lg (ν_{40} + 0.8)] \cdot d_{s h}^{2} \cdot n \cdot 10^{- 7}

Symbol	Description	Unit
P_VD	Power loss at the seal	W
ϑ_Oil	Oil operating temperature	°C
ν₄₀	Kinematic viscosity of the lubricant at 40°C	mm²/s
d_sh	Shaft diameter at the seal	mm
n	Speed of the shaft relative to the seal	1/min

Sources

Standards

ISO/TR 14179-1:2001(E): Gears - Part 1: Rating gear drives with thermal equilibrium at 95° C sump temperature, 2001
ISO/TR 14179-2:2001(E): Gears - Part 2: Thermal load-carrying capacity, 2001
DIN 3996:2019-09: Calculation of load capacity of cylindrical worm gear pairs with rectangular crossing axes, 2019
DIN 31652-1:2017-01: Plain bearings - Hydrodynamic plain journal bearings under steady-state conditions - Part 1: Calculation of circular cylindrical bearings, 2017
DIN 31653-1:1991-05: Plain bearings; hydrodynamic plain thrust bearings under steady-state conditions; calculation of pad thrust bearings, 1991
DIN 31654-1:1991-05: Plain bearings; hydrodynamic plain thrust bearings under steady-state conditions; calculation of tilting-pad thrust bearings, 1991
DIN 31657-1:1996-03: Plain bearings - Hydrodynamic plain journal bearings under steadystate conditions - Part 1: Calculation of multi-lobed and tilting pad journal bearings, 1996

Books, Catalogs, Instruction Manuals

SIMRIT: Radialwellendichtringe, Katalog Nr. 100, 1976
ESCHMANN, P. u. a.: Die Wälzlagerpraxis. Oldenburg München-Wien, 1978
NIEMANN, G., WINTER, H.: Machine Elements, Vol. 3, Berlin: Springer, 1983
FREUDENBERG: Simmering/Radial-Wellendichtringe, Katalog Nr. 100 Ausgabe 1/86
ARPM OS-15: Measuring Radial Lip Seal Torque and Power Consumption, Association for Rubber Products Manufacturers, 1986
LINKE, H.: Stirnradverzahnung, 2. Auflage, Carl Hanser Verlag München Wien, 2010
SKF: Rolling bearings, catalogue, PUB BU/P1 17000/1 EN, 2018
SCHAEFFLER: Rolling bearings, catalogue, HR 1, 2018
TIMKEN: Engineering manual bearings, catalogue, 2011
WTplus: FVA-EDV Programm WTplus, Version 2.2.1, Benutzeranleitung, 2016

Dissertations and Publications

OHLENDORF, H.: Verlustleistung und Erwärmung von Stirnrädern, TH München, Diss., 1958
ARIURA, Y.: Lubricant churning loss in spur gear systems, JSME Vol. 16, pp. 881 -891, Veröffentlichung, 1973
WALTER, P.: Anwendungsgrenzen für die Tauchschmierung von Zahnradgetrieben, Plansch- und Quetschverluste bei Tauchschmierung, Universität Stuttgart, Diss., 1982
MAUZ, W.: Hydraulische Verluste bei Tauch- und Einspritzschmierung von Zahnradgetrieben, Universität Stuttgart, Diss., 1985
WECH, L.: Untersuchungen zum Wirkungsgrad von Kegelrad- und Hypoidgetrieben, TU München, Diss., 1987
BUTSCH, M.: Hydraulische Verluste schnelllaufender Stirnradgetriebe, Universität Stuttgart, Diss., 1989
SCHLENK, L.: Untersuchungen zur Fresstragfähigkeit von Großzahnrädern,TU München, Diss., 1995
BARTON, P. M.: Tragfähigkeit von Schraubrad- und Schneckengetrieben der Werkstoffpaarung Stahl/Kunststoff, Ruhr-Universität Bochum, Diss., 2000
DOLESCHEL, A.: Wirkungsgradberechnung von Zahnradgetrieben in Abhängigkeit vom Schmierstoff, TU München, Diss., 2002
WASSERMANN, J.: Einflussgrößen auf die Tragfähigkeit von Schraubradgetrieben der Werkstoffpaarung Stahl/Kunststoff, Ruhr-Universität Bochum, Diss., 2005
WIMMER, A.: Lastverluste von Stirnradverzahnungen - Konstruktive Einflüsse, Wirkungsgrad-maximierung, Tribologie, TU München, Diss., 2006
WENDT, T.: Tragfähigkeit von Schraubradgetrieben mit Schraubrädern aus Sintermetall, Ruhr-Universität Bochum, Diss., 2008
PECH, M.: Tragfähigkeit und Zahnverformung von Schraubradgetrieben der Werkstoffpaarungen Stahl/Kunststoff, Ruhr-Universität Bochum, Diss., 2011
MILTENOVIC, A.: Verschleißtragfähigkeitsberechnung von Schraubradgetrieben mit Schaubrädern aus Sintermetall, Ruhr-Universität Bochum, Diss., 2011
SUCKER, J.: Entwicklung eines Tragfähigkeitsberechnungsverfahrens für Schraubradgetriebe mit einer Schnecke aus Stahl und einem Rad aus Kunststoff, Ruhr-Universität Bochum, Diss., 2012

Forschungsvereinigung Antriebstechnik e.V. (FVA), Frankfurt/Main

MAUZ, W.: FVA-Heft 185: Zahnradschmierung-Leerlaufverluste, FVA Nr. 44 III, Abschlussbericht, 1985
MAURER, J.: FVA-Heft 432: Ventilationsverluste, FVA Nr. 44 VI, Abschlussbericht, 1994
SCHLENK, L.: FVA-Heft 443: Größeneinfluss Fressen, FVA-Nr. 166 I, Abschlussbericht, 1995
KETTLER, J.: FVA-Heft 639: Planetengetriebe-Sumpftemperatur, FVA-Nr. 313 I, Abschlussbericht, 2000
DOLESCHEL, A.: FVA-Heft 664: Wirkungsgradtest, FVA-Nr. 345 I, Abschlussbericht, 2001
GEIGER J.: FVA-Heft 959: Validierung WTplus, FVA-Nr. 69 V, Abschlussbericht, 2010
HAGEMANN, T.: FVA-Heft 996: Verbesserte Radialgleitlagerberechnung, FVA-Nr. 577 I, Abschlussbericht, 2011
PFEIFFER P.: FVA-Heft 1184: Radialkippsegmentlager Ölzuführungseinfluss, FVA-Nr. 677 I, Abschlussbericht, 2016
SEDLMAIR M.: FVA-Heft 1208: Erweiterung WTplus, FVA-Nr. 69 VI, Abschlussbericht, 2017
OEHLER, M.: FVA-Heft 1226: Schneckengetriebewirkungsgrade, FVA-Nr. 729 I, Abschlussbericht, 2017
JURKSCHAT, T.: FVA-Heft 1223: Verlustleistung von Stirnradverzahnungen, FVA-Nr. 686 I, Abschlussbericht, 2017
FINGERLE A.: FVA-Heft 1282: Durchgängige Berechnung gleitgelagerter Welle-Lager-Systeme, FVA-Nr. 668 II, Abschlussbericht, 2018
SEDLMAIR M.: FVA-Heft NA: Innenverzahnungen - Reibung und Wärme, FVA-Nr. 584 II, ongoing project, 2022

In this section:

KnowledgeBase

Power loss

Gear losses

Load-dependent gear losses for cylindrical gears

Tooth loss factor according to OHLENDORF

Tooth loss factor according to TALBOOM

Local-geometric tooth loss factor according to WIMMER

Average gear friction coefficient according to SCHLENK

Average gear friction coefficient according to DOLESCHEL

Load-dependent gear losses for bevel/hypoid gears

Load-dependent gear losses for worm gear stages

Average gear friction coefficient according to DIN 3996:2019

Average gear friction coefficient according to DIN 3996:2012

Load-independent gear losses for cylindrical, bevel, and hypoid gears

Immersion lubrication

Load-independent gear losses with immersion lubrication according to MAUZ

Load-independent gear losses with splash lubrication according to WALTER

Injection lubrication

Squeeze losses according to MAUZ for vt < 60 m/s

Squeeze losses according to BUTSCH for vt > 60 m/s

Pulse losses according to AIURA for vt < 60 m/s

Pulse losses according to BUTSCH for vt > 60 m/s

Ventilation losses according to MAURER

Load-independent gear losses for worm stages

Rolling bearing losses

SKF 2020

SCHAEFFLER 2020

TIMKEN 2020

ISO 14179-2

Plain bearing losses

Combros R&A

Planet carrier losses

Single-plate planet carriers according to KETTLER

Dual-plate planet carriers according to KETTLER

Sealing losses

ISO 14179-1 (USA)

ISO 14179-2 (Germany)

LINKE

Sources

Search results

Squeeze losses according to MAUZ for v_t < 60 m/s

Squeeze losses according to BUTSCH for v_t > 60 m/s

Pulse losses according to AIURA for v_t < 60 m/s

Pulse losses according to BUTSCH for v_t > 60 m/s