KnowledgeBase

The main bearing geometry refers to geometry data that is available in the bearing manufacturer's catalog. Generally, this is limited to the following (calculation-relevant) parameters:

Knowledge of the internal geometry of the bearing (number of rolling elements, rolling element diameter, etc.) is required to calculate the rolling bearing stiffness and lifetime. However, this information is missing from the manufacturers' catalogs; therefore, the internal geometry of the bearing must be estimated. If the user does not explicitly define the internal geometry of the rolling bearing, the FVA-Workbench will estimate it based on available catalog data.

Algorithm for estimating the internal bearing geometry: The standards ISO 281 2007 and ISO 76 2006 specify formulas for determining the dynamic and static radial load ratings of rolling bearings based on internal geometry parameters. The algorithm for estimating the internal geometry of the bearing calculates the associated load ratings in an iterative process based on estimated geometry parameters, and compares them with the load ratings from the catalog. If the difference between the specified and calculated load ratings is greater than the termination tolerance, the geometry estimation is adjusted accordingly and a new iteration is started. Key variables of the iteration are the number and diameter of the rolling elements as well as the effective roller length for roller bearings. The concept of the algorithm is based on the approach from FVA 364, improved with additional consistency checks (no overlapping of the rolling elements, etc.). For premium bearings, a reduced dynamic load rating is used for the geometry estimation, as described on page 20 of the FVA 364 II final report.

The relevant parameters of the internal bearing geometry are described in more detail below:

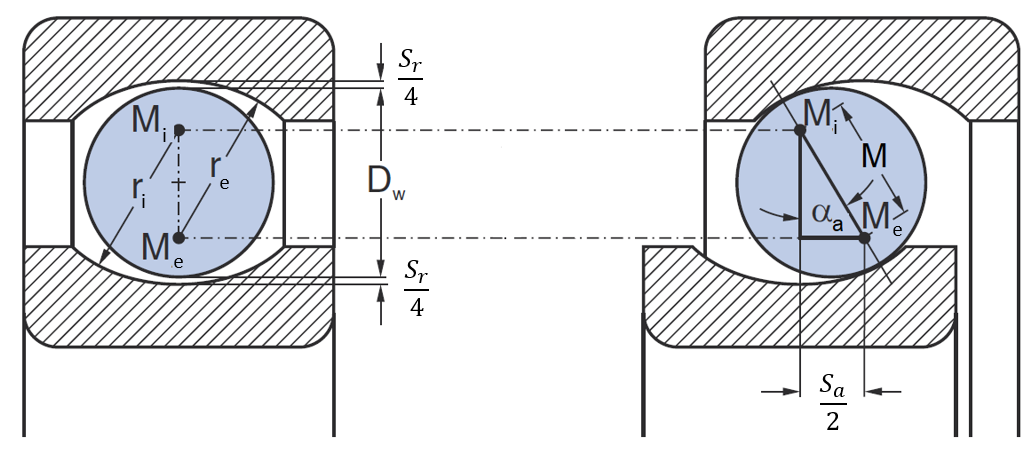
Pitch diameter: For ball bearings, the pitch circle corresponds to the centers of a row of balls. For roller bearings, it is the diameter of the circle that intersects the roller axis in the center of the rollers of a bearing row. As the diameter of the bearing raceway is not specified in the bearing catalogs, the pitch diameter can be approximated by the average value of the diameters of the inner and outer rings of the bearing: D_pw = 0.5(d+D)

Rolling element diameter: For ball bearings, the diameter of the ball. For roller bearings, the rolling element diameter is determined at the center of the rolling length.

Number of rolling elements: Specifies the number of rolling elements in a rolling element set/bearing row.

Effective roll length: The theoretical maximum length of the shortest line of contact between a roller and the raceway. This is typically either the distance between the theoretical sharp edges of the roller minus the edge distances or the width of the raceway minus the grinding undercuts, whichever is smaller.

Groove radius of the inner and outer ring raceways: The following table lists the formulas used for the groove radius of the inner and outer ring raceways in the FVA-Workbench, based on ISO 16281:

Spherical roller outer radius: In spherical roller bearings, the rolling element is a crowned circular shape. The outer radius of the spherical roller corresponds to the radius of this circle. According to ISO 16281, a value of R_p= 0.97 r_e is used for the spherical roller outer radius.

Distance between the bearing rows: For double-row bearings only: specifies the distance between the centers of the rolling elements of both rows. For self-aligning bearings, d_R=D_pw tan(α); otherwise, an estimate of d_R=0.5 B is used.

Bearings without rings: For needle roller bearings and cylindrical roller bearings, one or both of the raceways may be specified without a bearing ring. For catalog needle roller bearings, this is automatically considered based on the catalog designation. This has an influence on the determination of the bearing inner geometry. This is not considered in the calculation according to FVA 364.

An interference is calculated for the mating parts (shaft-bearing and bearing-casing). The roughness smoothing factor must be considered for calculation of the effective interference between the mating parts. The higher the surface roughness of the mating parts, the greater the smoothing effect, which leads to a loss of interference. The smoothing effect of the bearings is negligible, as the bearing rings are hardened and precision ground, and have a finer surface compared to the shafts and casing. In the case of a press fit on the shaft, the effective interference on the inner ring can be determined as follows:

In the case of an interference fit of the outer ring in the bore, the effective interference can be determined by:

The smoothing factor can be specified by the user. In addition to smoothing, the interference can be reduced by non-uniform thermal expansion. When the outer ring and the casing or the inner ring and the shaft are made of different materials, the operating temperatures change the original interference. Generally, the bearing casing is made of a lighter material than the outer bearing ring (higher coefficient of thermal expansion), which leads to reduced interference at operating temperature. The reduction of the interference due to thermal expansion can be calculated as follows:

where d is the joining diameter, α_e, α_i the coefficients of thermal expansion of the outer and inner materials, and ΔT_op the difference between the reference temperature and operating temperature (20°).

In the case of an interference fit between the shaft and inner ring, the raceway of the inner ring is deformed and thus expands, which leads to a reduction of the internal bearing clearance. Similarly, in the case of an interference fit between the outer ring and the casing bore, the outer raceway narrows, which also reduces the internal bearing clearance. This effect is described in "ROLLING BEARING ANALYSIS" by Harris, among others. It was implemented in FVA 364 III, from which the following figure is taken:

Figure 26.

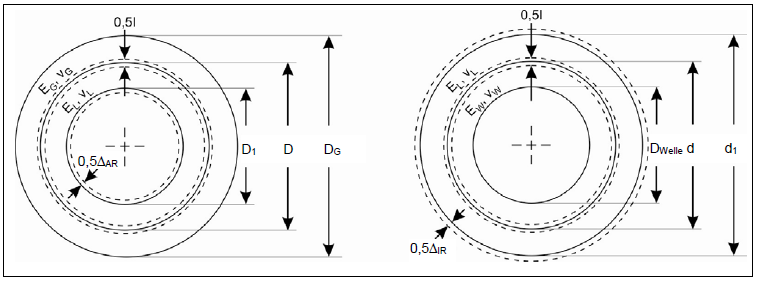
Narrowing of the outer ring raceway (left) and widening of the inner ring raceway (right)

The calculation is based on the theory of elastic rings. The reduction of the clearance is described in the following formulas:

where I is the corresponding effective interference, D_Welle = inner diameter of the shaft, d = outer diameter of the shaft/inner diameter of the bearing, d₁ = inner raceway diameter, D₁ = outer raceway diameter, D = outer bearing diameter/bore diameter, D_G = equivalent casing diameter. Furthermore E_L, ν_L are the material parameters of the bearing (or bearing rings), E_W, ν_W the material parameters of the shaft, and E_G, ν_G the material parameters of the casing.

For many bearing types, it is not immediately clear which "raceway diameter" should be used. The detailed calculation uses the following convention: if the rolling element runs in a groove of the raceway, the "contact point" between the rolling element and raceway under the nominal contact angle is used. The same consideration is made with the midpoint of the roller for double-row tapered roller bearings. If the internal clearance of the bearing prior to installation is neglected, then:

For the detailed calculation according to FVA 364, the following simplified formulas are used to determine the raceway diameters:

Note: in most applications, the casing is not a hollow cylinder, but rather a more complex construction. Thorough consideration of such complex geometry requires extensive modeling and calculation details. The FVA-Workbench simplifies this by using the specified outer diameter of an equivalent hollow cylinder casing.

Simplified calculation according to FVA 364: With the "simplified calculation acc. to FVA 364" switch, the bearing rings are simplified as "stiff," and the determined interference (or loose fit) of the rings is directly considered as deformation of the raceways and calculated with the bearing clearance.

Temperature distribution in the bearing is uneven during operation. According to "Die Wälzlagerpraxis" ("Ball and Roller Bearings: Theory, Design, and Application") by Brändlein et. al., the temperature of the inner ring is 5-10 K higher than the outer ring (if the casing is air cooled, this difference increases to 15-20 K). This temperature difference causes the inner ring and the rolling elements to expand more than the outer ring, which leads to a reduction of the radial bearing clearance.

Hence the radial bearing clearance is reduced by:

where ΔT_ie= temperature difference between inner ring and outer ring, α_ring = 12e-6/K thermal expansion coefficient of the bearing ring, α_W = 12e-6/K (steel) resp. α_W = 3e-6/K (ceramic) thermal expansion coefficient of the rolling elements, D_W = diameter of the rolling elements, d₁ = inner ring raceway diameter.

When using the calculation according to FVA 364, the reduction in bearing clearance due to this temperature difference for steel bearings is approximated using the mean bearing diameter according to the SKF catalog:

Tolerance classes only specify an interval of permissible values. When specifying bearing tolerances, the corresponding combination of minimum and maximum dimensions can lead to large differences in the calculation of the operating clearance. For this reason, a mean, minimum, and maximum operating clearance are calculated. The user can choose which of these values is used for the subsequent stiffness and rating life calculations.

In the detailed calculation, the mean interference is calculated as the most likely interference according to findings from FVA 736 I (rolling bearing tolerances). Due to manufacturing deviations, there is a high probability that the actual dimension is one third of the tolerance zone from the machining side.

In the calculation according to FVA 364, the mean interference is determined as the arithmetic mean between the minimum and maximum interferences.

The following section describes the formulas for converting radial to axial clearance, or vice-versa, depending on the type of rolling bearings.

Deep groove ball bearings: The following relationships can be derived from the figure below:

Conversion of radial to axial clearance:

Conversion of axial to radial clearance:

2-row angular-contact ball bearings/four-point ball bearings/self-aligning ball bearings/spherical roller bearings:

Consider a rolling element in three positions, with the outer ring fixed: The midpoint of the rolling element (or, for spherical roller bearings, the center of the of the outer radius of the roller) is labeled M_WK; more precisely, M_WK,α refers to a concentric position at which the rolling element is located exactly on the pitch circle, and the outer and inner rings are the same distance from the rolling element. Furthermore, M_WK,r refers to the position at which the rolling element was moved in the radial direction until it made contact with the outer raceway, and M_WK,a refers to the position at which the rolling element was moved in the axial direction until it made contact with the outer raceway. The distance between the center of the outer raceway groove M_e and M_WK,r, M_WK,a is defined by r_e - 0.5 D_W (or r_e - R_p for spherical roller bearings, where R_p is the outer radius of the spherical roller). Thus, for spherical roller bearings, the radius of the roller (0.5 D_W) is replaced by the outer radius of the spherical roller (R_p).

Conversion of axial clearance to radial clearance:

Conversion of radial clearance to axial clearance:

2-row/paired tapered roller bearings:

Conversion of axial clearance to radial clearance:

Conversion of radial clearance to axial clearance:

Calculation of the internal load distribution of radial and thrust ball bearings is based on ISO 16281 with extensions from FVA 364 and FVA 701. The following influences can be considered:

Neutral position of the rolling elements: A right-handed Cartesian u,v,w-coordinate system is established, with its origin in the bearing center (half width, on the axis of rotation). Its axes are defined parallel to the shaft-coordinate system; in particular, the u-axis corresponds to the axis of rotation. The radial position of the rolling elements is determined by D_pw. The operating clearance s_α is equally divided between the inner and outer raceways. Therefore:

For single-row bearings, the center of the rolling elements is on the radial plane through the bearing origin. The inner and outer rings (raceways) are positioned according to the axial force absorption of the bearing row, the contact angle, and the operating clearance. The sign (+/-) of the pressure angle is defined by the axial force absorption:  α>0 = positive axial force absorption, α<0 = negative axial force absorption. Thus, for bearings in an X-arrangement, α₁<0, α₂>0; in an O-arrangement, on the other hand, α₁>0, α₂<0. The following applies for the centers of raceway groove radii:

Note: A special consideration applies for purely axial (thrust) bearings. The operating clearance specifies the mobility of the bearing rings from one limit position to the another. While the radial operating clearance is once again divided between an "upper" and "lower" rolling element, the axial operating clearance acts fully on all rolling elements. Therefore, 0.25 s_α is generally used in the above formulas. For α=90°, this is replaced with 0.5s.

For double-row axial bearings, the centers of the rolling elements of the first row are shifted by -0.5 d_R in the axial direction, and those of the second row are shifted by +0.5 d_R. The values of u_e and u_i also change by -/+ 0.5 d_R accordingly. If a bearing ring is ovalized, the center of the corresponding raceway curvature at the circumferential angle is also shifted by the corresponding amount in the radial direction. The operating clearance, etc. always assumes a circular bearing ring.

Note: Four-point bearings are modeled as 2-row angular contact ball bearings in an O-arrangement, in which each rolling element is "cloned." With sufficient axial load (Schaeffler: F_a≥1.20F_r , SKF: F_a≥1.27F_r), the rolling elements contact the inner and outer raceways at one point each. In this case, only one of the two rows is load bearing. Four-point contact leads to high friction and thus increased wear; therefore, this operating point should be avoided. The mechanical model in the FVA-Workbench does not ensure that that the rolling elements and their clones are in the same position during four-point contact. A corresponding warning is issued.

Hertzian contact: The Hertzian theory can be applied for calculation of the forces acting on the individual rolling elements. As long as the contact surfaces are small and the convergence of both rolling elements is relatively low for their size, the bearing rings and the balls near the point of contact can be represented as elliptical paraboloids. According to Hertz, the contact force Q over the elliptical contact surfaces with the semi-axes a and b determines the normal pressure distribution p(x,y) and the maximum deflection δ

where Q is the contact force, E the modulus of elasticity, ν Poisson's ratio, Σρ the total curvature of both bodies, κ the ratio of the two half-axes of the Hertzian contact ellipse, and K(κ) and E(κ)the complete elliptical integral of the first and second kind.

Force equilibrium on the rolling element: Consideration of the radial, outward-acting centrifugal force Q_c results in different working pressure angles between the rolling element and the inner (α_i) or outer (\(α_e) raceways. The following equilibrium of force applies for the rolling bearing forces on the inner and outer raceways Q_i, Q_e (see FVA 701 III final report):

The centrifugal force of a ball is calculated as:

Note: Frictional effects between the rolling element and raceway along with gyroscopic effects play a minor role and are neglected, as in FVA 701 III.

Resulting bearing forces: F_u, F_v, F_w are the sum force components from the shaft acting on the inner ring. The following applies (pay particular attention to the sign convention for α_i and α_e):

Resulting tilting moment: Contact forces acting between the inner ring of the bearing and the rolling elements cause tilting moments about the bearing center if the line of action of the force does not go through the center of the bearing. To determine the resulting tilting moment from the inner or outer ring contact, the respective contact force can be shifted along the line of action to the center of the rolling element.

Let P_WK be the current position of the center of the bearing and r_P the distance between the centers of the bearing and rolling element. Define the coordinate system u, r, s; where u corresponds to the u-axis of the bearing, r is the radial vector associated with the position angle of the rolling element φ, and s is the cross product of the two. Let ψ_WK be the position angle of P_WK about s from the r-axis. Then, the force Q_WK,i which acts from the inner raceway onto the rolling element causes the moment M_ψWK about the s-axis:

where the effective share of the tangential force is determined by

Finally, the formulas for the resulting tilting moment in the bearing are as follows:

Note: In ISO 16281 and some other publications, various simplifications are made in the calculation of the tilting moment. Most use the following formula:

Thus, the pitch circle radius is used as the lever arm, independent of the exact point of contact and the position of the rolling element under load. The tangential force which causes the moment is also usually not equal to the axial force.

Calculation of the internal load distribution of radial and axial roller bearings is based on ISO 16281 with enhancements from FVA 364 and FVA 701. The following influences can be considered:

Neutral position of the rolling elements: The geometric center M of the rolling element is the starting point for all calculations. Its radial position is determined by the pitch circle diameter D_pw, the axial position corresponds to the axial position of the bearing row (0 for single-row bearings, 0.5 d_R for double-row bearings). At M, the rolling element has the diameter D_W (measured perpendicular to the roller axis).  Let α_n be the nominal contact angle = contact angle at the outer ring contact, and ε the semicone angle of the roller (ε=0 if there are no tapered roller bearings). The value for the contact angle at the inner ring contact is α_n-2ε, and the longitudinal axis of the roller is tilted by the angle α_n-ε. The center of the running surfaces on the inner and outer rings are designated P_i and P_e respectively. The corresponding diameters (taking the operating clearance into consideration) can be calculated as:

Similarly, the axial position of P_i and P_e can be determined by offsetting M by the term sin(|α_n|-ε)( 0.5D_W + 0.25 s_α). The equivalent cylindrical diameter of the roller to be used for calculation of the contact is calculated as cos(ε)D_W.

Disc model: In general, the Hertzian and Palmer's equations cannot be directly applied for roller bearings. The Hertzian equations only apply for contact between cylinders of an infinite length. Palmgren's equation for steel bearings considers the finite dimensions of the rolling elements, but only applies for a centric load on the roller:

where δ represents the total deflection of the roller and Q the resulting contact force (for example, compare ISO 16281 or AB FVA 364 II Section 2.9.2). The disc model according to ISO 16281 is typically used in order to be able to consider effects such as tilting of the roller, profiling, rib contact, centrifugal force, etc. For calculation of the deflection, the roller is divided into n_s equal slices; according to ISO 16281, the minimum number of slices should be at least n_s = 30. The corresponding line load for the operating conditions of the bearing are determined for every disc contact. This is done using the disc deformations and Palmer's equation for the discs. The disc method assumes a two-dimensional stress state for the individual discs to calculate the line loads. This ignores the cross-influences, and thus the shear stresses between the discs. Therefore, in the disc method the individual discs are pushed together independent of the deflection of the neighboring discs.

The deformation-force relationships from R. Teutsch and B. Sauer “An alternative slicing technique to consider pressure concentrations in non-Hertzian contacts", J. Tribol 126(3), 436-442 (2004), can be used as an alternative to the above relationship of ISO 16281 (Palmgren). These are based on a regression model which uses an explicit formula to approximate the implicit deformation-force relationship for line contact established by Dinnik. In contrast to Palmgren, this formula explicitly considers the material characteristics, rolling element diameter and pitch circle diameter, and the thickness of the outer ring and the housing ring.

Force and moment equilibrium on the rolling element: The following influencing factors on the force equilibrium of a rolling element must potentially be taken into account in order to be able to consider all use cases:

The following applies to tapered roller bearings in axial and radial force equilibrium:

where Q_c represents the centrifugal force of the roller and Q_B,i/e the on-board force on the inner/outer ring. The general moment equilibrium is determined as:

where the prefixes (+/-) of the excentricity are determined such that e>0 at the exact point where the force causes a positive (rightward-turning) moment.

Resulting bearing forces and tilting moments: The forces and tilting moments resulting from the loading of the individual rolling elements are determined similar to the process described for ball bearings.

Consideration of the operating pressure angle for spherical roller bearings

As described in ISO/DIS 16281:2023 A.3.3, when calculating spherical roller bearings, the operating contact angle of each rolling element is taken into account when calculating the load distribution in the bearing. This leads in particular to a centered load distribution on each roller. The spherical roller bearing therefore does not generate a tilting moment even when tilted and under axial load.

The International Organization for Standardization (ISO) is the international association of standards bodies (e.g. DIN, ANSI, …). 164 countries are currently represented in the ISO (121 full members, 39 corresponding members, and 4 observers). For more information, see refer to the ISO website at www.iso.org.

There are 249 different Technical Committees (TC). TC 4 is responsible for rolling bearings, and rolling bearing rating life is discussed in Sub Committee (SC) 8. ISO 281 is developed in ISO/TC 4/SC 8. whose secretariat is administered by the German Institute for Standardization (www.din.de). The responsible German body is working committee NA 118-01-08 AA, "load ratings and rating life" in the Rolling and Plain Bearings Standards Committee (Normenausschuss Wälz- und Gleitlager, NAWGL).

Generally speaking, the application of standards is voluntary; standards are non-binding. Standards become legally binding when laws or legal regulations, such as EU directives, refer to them. Contractual partners may also specify the application of standards in their agreements.

The current version of ISO 281 is from 2007, and replaces the withdrawn standards ISO 281:1990 , ISO 281:1990/AMD 1:2000 , ISO 281:1990/AMD 2:2000, and ISO/TS 16799:1999. The current German version is DIN ISO 281:2010-10, and replaces the withdrawn standards DIN ISO 281:1993-01, DIN ISO 281:2009-01, DIN ISO 281/A1:2001-09, and DIN ISO 281/A2:2001-09.

Scope: "This International Standard specifies methods of calculating the basic dynamic load rating of rolling bearings within the size ranges shown in the relevant ISO publications, manufactured from contemporary, commonly used, high quality hardened bearing steel, in accordance with good manufacturing practice and basically of conventional design as regards the shape of rolling contact surfaces.

This document also specifies methods of calculating the basic rating life, which is the life associated with 90 % reliability, with commonly used high quality material, good manufacturing quality and with conventional operating conditions. In addition, it specifies methods of calculating the modified rating life, in which various reliabilities, lubrication condition, contaminated lubricant and fatigue load of the bearing are taken into account.

This International Standard does not cover the influence of wear, corrosion and electrical erosion on bearing life. This document is not applicable to designs where the rolling elements operate directly on the shaft or housing surface, unless that surface is equivalent in all respects to the bearing ring (or washer) raceway it replaces. Double-row radial bearings and double-direction thrust bearings are, when referred to in this document, presumed to be symmetrical." [DIN ISO 281:2010 Section 1]

Calculation scope: The central calculation variables for ISO 281 are:

To determine the nominal rating life L₁₀, the dynamic load rating of the bearing is compared with the equivalent dynamic load. The number and diameter of the rolling elements as well as the effective roller length for roller bearings have a significant influence on the determination of the dynamic load ratings according to ISO 281. The load ratings provided by the bearing manufacturers are used for the ISO 281 calculation in the FVA-Workbench. The equivalent dynamic load as a function of the radial and axial bearing forces is determined by:

where the load factors X and Y are automatically determined in the FVA-Workbench according to ISO 281 specifications.

The modified rating life considers the rating life coefficient a₁ for the reliability as well as the rating life coefficient a_ISO for the system analysis:

The rating life coefficient a₁ can be influenced by the choice of reliability to be considered. The rating life coefficient a_ISO is determined as a function of the fatigue limit load C_u, the contamination (contamination coefficient e_C), the lubrication conditions (viscosity ratio κ), and the bearing load P.

Limitation: The influence of the bearing clearance, tilting under general operating conditions, etc. are only considered in ISO 281 by their influence on the effective bearing forces. More precise consideration of the bearing rating life, taking the internal load distribution of the rolling bearing into account, is provided by ISO/TS 16281 (DIN 26281).

Geometry dependence for ball bearings: Even with a specified fixed bearing load (forces), the rating life according to ISO 281 can change due to changes to the internal geometry. This is due to the geometry-dependent load factors in ISO 281(Table 3). Therefore, the equivalent dynamic load P and thus the rating life coefficient a_ISO are geometry-dependent.

The current version of ISO/TS 16281 was published in 2008 and a corresponding corrigendum was issued in 2009. It will soon be replaced by a fundamentally revised version and upgraded to the full ISO standard. This is currently available as draft ISO/DIS 16281:2023. DIN 26281:2010 is the German-language version of ISO/TS 16281:2008 and replaces DIN ISO 281 Supplement 4 from 2003.

Scope:

This document defines the calculation of the modified reference rating life taking into consideration lubrication, contamination, and fatigue load limit of the bearing material, as well as tilting or misalignment, operating clearance of the bearing and internal load distribution on rolling elements. The calculation method provided in this document covers influencing parameters additional to those described in ISO 281.

The general directions and limitations given in ISO 281 apply to this document. The calculation methods pertain to the fatigue life of the bearings. Other mechanisms of failure, like wear or microspalling (graystaining), lie outside the scope of this document.

This document applies to single- and multi-row radial and thrust ball bearings, subjected to radial and axial load and with radial clearance and tilt taken into account. It also applies to single- and multirow radial and thrust roller bearings, subjected to radial and axial load and with radial clearance, edge stress and tilt taken into account. References to methods for the analysis of the internal load distribution under general load are given.

The analysis of internal load distribution and modified reference rating life for bearings of a more complex geometry can be derived from the formulae given in this document. For these bearings, the load distribution for each individual row has to be considered.

The calculation of load distribution and basic reference rating life is also applicable to hybrid bearings, using the dynamic load ratings per ISO 20056-1. The calculation of the modified reference rating life is not applicable to hybrid bearings.

Implementation in the FVA-Workbench:

The necessary extension of the calculation methods in ISO/TS 16281:2008 to general operating conditions and more complex bearing geometries is based on the FVA Research Projects 364 and 701. For example, this includes the extension of the method to double-row bearings or the exact determination of the dynamic load rating of a laminae for spherical and tapered roller bearings. The calculation methods for determining the internal load distribution in the bearing also significantly extend the scope of ISO 16281, for example by taking centrifugal force into account. Details on determining the internal load distribution are documented in the stiffness section.

With FVA-Workbench 9.2, the adaptations and extensions of ISO/DIS 16281:2023 are now also taken into account.

Calculation scope:

In addition to the detailed definition of the internal load distribution (and thus the bearing operating points/the resulting bearing forces and moments), the central result variables in ISO 16281 are the:

The most signification difference to the calculation according to ISO 281 is that the load and load capacity of the individual rolling element contacts are used to determine the rating life. For ball bearings, the dynamic load rating of the individual contact for the inner and outer ring is also determined from the load rating of the bearing and the geometric parameters. In contrast, the dynamic equivalent loads of the inner and outer ring contact are determined from the effective rolling element forces. For rolling bearings, the dynamic load rating of a roller washer on the inner and outer ring is determined based on the load rating of the bearing and the geometric parameters. This is then compared to the dynamic equivalent load rating of a washer on the inner and outer ring. The dynamic equivalent reference load of the bearing is then obtained from the load rating of the bearing and the calculated nominal reference rating life. The rating life coefficient a₁ for the reliability and rating life coefficient a_ISO are also used to determine the modified reference rating life. These are determined according to the specifications in ISO 281, but the dynamic equivalent reference load (ball bearings) or the dynamic equivalent load of the bearing washer (roller bearings) are taken into account for determining a_ISO.

Changes and extensions ISO/DIS 16281:2023

Determination of the load distribution and pressure of roller bearings

As described in the roller bearing stiffness section above, the disc method ignores cross influences between the discs, and the deflection of one disc has no influence on the neighboring discs. Therefore, this method cannot be used to determine any edge pressures that may occur (due to insufficient profiling/excessive tilting), in particular.

ISO/DIS 16281:2023 offers the possibility of correcting the load distribution determined using the disk method as a simple approximation using the empirical load increase function according to equation (94) in order to take into account the effect of the shear stress influence and any resulting edge stresses. This approximation is only applicable for the approximation profile according to ISO 16281 and under the conditions of medium load and tilting of the bearing of less than 4 angular minutes. A more sophisticated method is recommended for general calculations.

Alternatively, a calculation method can be used that also takes into account the shear stress influence of the laminae. This allows edge effects to be calculated for any roller profile and taken into account in the service life calculation. The influence of the load on one laminae on the deformation of the neighboring laminae is also taken into account. The current bearing calculation of the FVA-Workbench uses the influence coefficient matrix from R. Teutsch and B. Sauer, "An alternative slicing technique to consider pressure concentrations in non-Hertzian contacts", J. Tribol 126(3), 436-442 (2004).